数论题目

素数个数

 

样例输入

4
2 11
2 98
2 1000000
999999000000 1000000

样例输出

6
25
78498
36400



直接上代码吧，注释很全了

#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int N = 1e6 + 5;
ll n, m, pr[N], tot, s[N];
bool vis[N];

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        scanf("%lld%lld", &n, &m);
        memset(vis, 0, sizeof vis);
        ll total = m + 1;//将n到n+m的数全认为是质数，也就是这个区间上数的个数总数 
        //区间里数的总数减去该区间所有合数，最终就是质数个数 
        //下面开始找合数 
        for (ll i = 2; i <= 1e6 && i <= n + m; i++)//从2到1e6枚举因数 
        //因数枚举的范围2-1e6，i<=n+m是一个小剪枝 
            for (ll j = (n / i) * i; j <= n + m; j += i)//(n/i)*i最接近n的i的倍数 
            //j是枚举n到n+m之间i的倍数，他有i这个因子，所以他就是合数了，标记为访问过，防止重复访问 
                if (j >= n && j != i && !vis[j - n]){
                    //j>=n就排除了(n/i)*i<n的情况 
                    //j != i是因为，当i=j时，不足以证明他是合数 
                    vis[j - n] = 1;//标记为访问过 
                    total--;//找到一个合数，减掉该合数 
                }
        printf("%lld
", total);
    }
}

 

---

视野

样例1输入

10
1
2
3
4
5
6
7
8
9
10

样例1输出

1
3
7
11
19
23
35
43
55
63

 

---

 

因为左上右下两部分是对称的，所以只求一部分即可，最后答案乘以2

但是，要知道对角线是只有一条的，对角线上只有一个点，

所以最后乘了2的答案要减去1

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;

int T,C,phi[N], prime[N], tot;
bool vis[N];
long long ans;

void getprime(){ //欧拉函数 
    phi[1]=1;
    for (int i = 2; i <= 1e6; i++) {
        if (!vis[i]) {
            prime[++tot] = i;
            phi[i] = i - 1;
        }
        for (int j = 1; j <= tot && i * prime[j] <= 1e6; j++) {
            vis[prime[j] * i] = 1;
            if (i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            } else
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

int main() {
    getprime();
    scanf("%d", &T);
    while (T--) {
        ans=0;
        scanf("%d", &C);
        for(int i=1;i<=C;i++)
            ans+=phi[i];
        ans=ans*2-1;//或者写成(ans-1)*2+1 (因为其他地方都有对称的，而对角线上只有一个，所以要-1) 
        printf("%lld
", ans); //??
    }
}

 

---

 

Hankson的趣味题

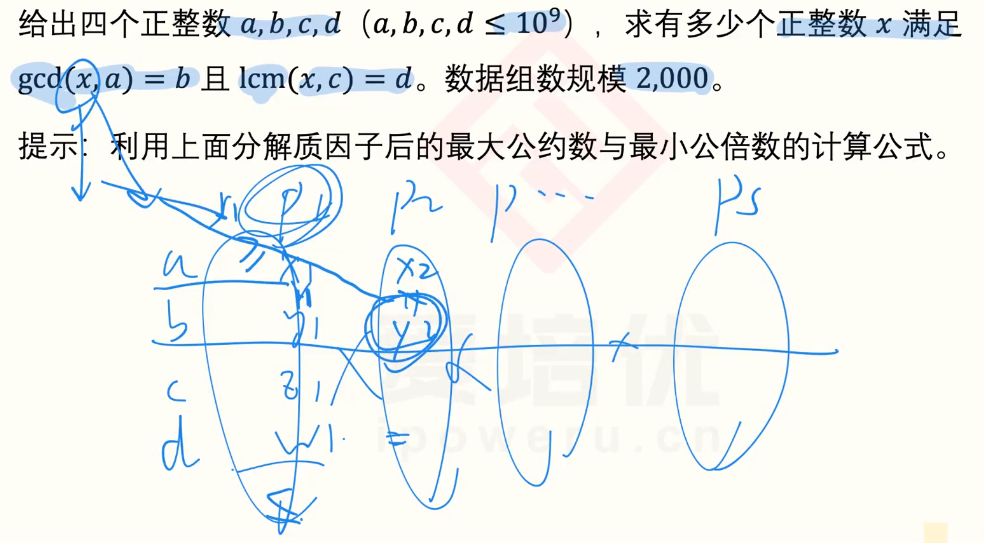
分解质因数做就ok啦

图中，

p1,p2,p3.....是a,b,c,d全部的质因数

x1,y1,z1,w1....是幂次（不含就记为0）（也就是该数含有多少次的该列的质因子）

gcd的话，我们来看a,b

他是有个≥的界或=的界

若x1=y1，则x分解出来的p1的幂次≥x1即可

若x2≠y2，则x分解出来的p2的幂次要刚好等于y2

（因为呢，b是a与x的gcd嘛，b的某质因数的幂次肯定≤a的该质因数的幂次，

若x2≠y2，则y2一定≤x2，嗯

x该质因数的幂次不能>y2，要是大于，最大公约数b的该质因数的幂次就会比此时的y2大了）

lcm的话，就看c,d

他有个≤的界或=的界

算法同上啦，仔细分析一下就好啦（其实是我懒得去想了嘿嘿）

/*存在x使得： x 和 a0的最大公约数是 a1
  x和b0的最小公倍数是b1 ，求x的个数
   
 →x % a1 = 0, a0 % a1 = 0（确定）, gcd(x,a0) = a1;  公约数 
   b1 % x = 0, b1 % b0 = 0（确定）, lcm(x,b0) = b1;  公倍数 */
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int n,a0,a1,b0,b1;

int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}

int pd(int x){  
    if(x%a1==0) 
        return(gcd(x/a1,a0/a1)==1 && gcd(b1/b0,b1/x)==1);
    return 0;
}

int main(){
    scanf("%d",&n);
    while(n--){
        ll ans=0;
        scanf("%d%d%d%d",&a0,&a1,&b0,&b1);
        for(int i=1;i*i<=b1;i++){
            if(b1%i==0){  //是公倍数 
                ans+=pd(i);
                if(b1!=i){
                    int ii=b1/i;
                    ans+=pd(ii);  //特判 1 1 1 1的状况 
                }
            }
        }
        printf("%lld
",ans);
    }
    return 0;
}  

lhc  dalao的分析：https://www.luogu.org/blog/violet2333/hankson-di-qu-wei-ti

这位dalao证明了一个超棒地结论：https://blog.csdn.net/nuclearsubmarines/article/details/77603154

 

---

 

麻球繁衍

这题必须纪念一下

各种渠道各种求助dalao，弄了几个小时才明白的

---

样例1输入

3 1 1
0.33
0.34
0.33

样例1输出

0.3300000

样例2输入

3 1 2
0.33
0.34
0.33

样例2输出

0.4781370

---

先说明：

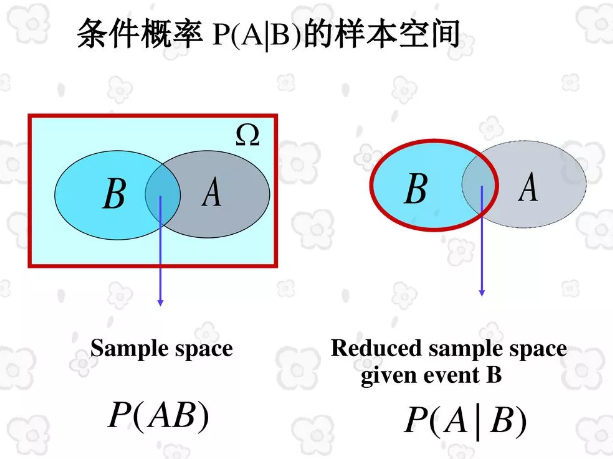
然后 

 全概率公式

  

 

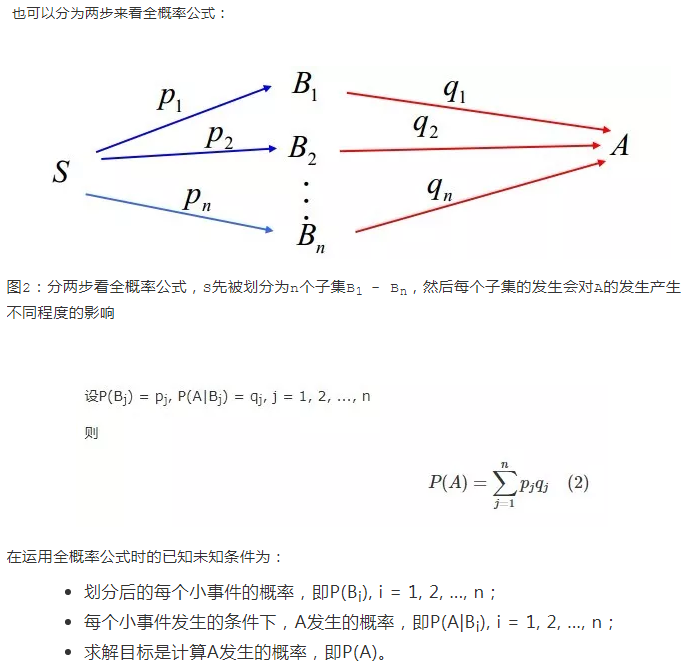
好了，全概率公式就补充这些

---

下面是该题的做法

读题知：

今天的肯定都是昨天新生的，今天这些也肯定到不了明天，今天就死掉了，
明天的是今天的某些生的，生不生概率是一定的，且每个生的个数是一定的

今天死光了说明前一天死完了，所以可用前一天死亡的概率就可以来递推今天全部死亡的概率

询问的是m天内所有生物都死的概率（包括m天前死亡的情况）

每个麻球都是独立的，而且会在当天死亡，

每个麻球和它的后代死亡的概率也是独立的

因为麻球的各种活动都互不影响，所以现在只考虑一只麻球

 再来一遍全概率公式，展开一下： P(A)=P(B1)*P(A|B1)+P(B2)*P(A|B2)…P(Bn)*P(A|Bn)

因为这j个后代的死亡是独立的，而每个死亡的概率都是f(i-1)（今天死光了说明前一天死完了，所以可用前一天死亡的概率就可以来递推今天全部死亡的概率），

因此根据乘法公式，j个后代全部死亡的概率为f(i-1)^j 。

同理，由于一开始共有k只麻球，且各只麻球的死亡是独立的，由乘法公式，最终答案是f(m)^k

---

//每只麻球是独立的，k只的答案是一只的k次方。
//同样，生出的每只麻球也是独立的，单独考虑即可。
#include<bits/stdc++.h>
#define N 1000 + 10
using namespace std;

int n, k, m;
double p[N], f[N];

int main() {
    scanf("%d %d %d", &n, &k, &m);
    for (int i = 0; i < n; i++) 
        scanf("%lf", &p[i]);
    f[0] = 0, f[1] = p[0];
    for (int i = 2; i <= m; i++) {
        f[i] = 0;
        for (int j = 0; j < n; j++) 
            f[i] += p[j] * pow(f[i - 1], j);
    }
    printf("%.7lf
", pow(f[m], k));
    return 0;
}

---

拓展φ 

样例输入

11 10

样例输出

10
5
7
5
8
3
9
5
7
4
10

 （嘻嘻嘻，求助了几位dalao才弄懂得，必须要纪念一下）

这道题就是利用容斥原理啊

#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int N = 100005;
int n, prime[N], tot, cnt;
bool vis[N];
ll m, num[N], ans;

void getprime() {
    for (int i = 2; i <= n; i++) {
        if (!vis[i])
            prime[++tot] = i;
        for (int j = 1; j <= tot && i * prime[j] <= n; j++) {
            vis[i * prime[j]] = true;
            if (i % prime[j] == 0)
                break;
        }
    }
}

void work(int n) {
    for (int i = 1; i <= tot && prime[i] <= n; i++) {
        int x = prime[i];
        if (n % x == 0) {
            num[++cnt] = x;// 
            while (n % x == 0)
                n /= x;
        }
    }
}

//减掉与其不互质的，余下的就是互质的个数啦 
//不互质的咋减呢，找他的质因子喽，同样有这个质因子的肯定跟他不互质啦
void dfs(int a, int p, int s) {//p约数，s为正负1(加还是减) 
    if (!a) {
        ans += (ll)s * m / p; // m/p是m中p的倍数的个数 
        return;
    }
    //看质因数个数，一个->加，两个->减，三个->加... 
    dfs(a - 1, p, s);
    dfs(a - 1, p * num[a], -1 * s);
    /*比如有因数3,4,5 
                     1
                  /     
                /         
               3            1
             /           /    
           3*4    3      4     1
          /     /     /    / 
      3*4*5 3*4 3*5 3  4*5 4 5   1
    */
}

signed main() {
    cin >> n >> m;
    getprime();//质数表 
    for (int i = 1; i <= n; i++) {
        ans = 0;
        cnt = 0;//质因子个数 
        work(i);//求i的质因子个数 
        dfs(cnt, 1, 1);
        printf("%lld
", ans);
    }
}