题目链接https://www.acwing.com/problem/content/1512/
一个街道两侧有两栋楼，现在有如图所示两楼梯 (x,y)。
两个楼梯分别如图放置。
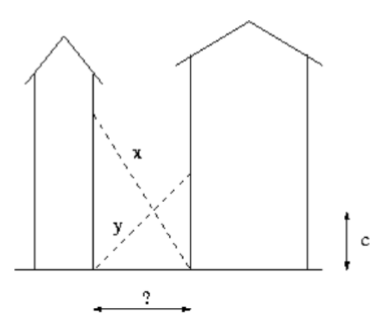已知两个楼梯的长度和他们交点离地面的高度，求两栋楼之间的距离。
#输入格式
一行三个实数，分别表示 (x,y,c)。
#输出格式
输出共包含 1行。
即所求的两栋楼之间的距离，保留三位小数。
#数据说明
$0<a,b,c<2500$
保证数据合法。
#输入样例：
30 40 10
#输出样例：
26.033
分析
这个看起来不是那么难，第一眼肯定是推公式然后$O(1)$输出，我也是这么想的，但发现根本推不出来！可能是我数学太差了？所以考虑用计算机来算这个数学题，这个问题其实是有单调性的，由$x,y,c$推出距离$s$很不好推，但由$x,y,s$推$c$却是十分简单。
而观察可以发现，当两个楼之间距离过小时，因为$x,y$一定，所以$c$一定会更高，过大时就会更低，根据这个二分答案就行。
那么，$c$怎么求呢？除$s$外的两条直角边的倒数和跟$c$的倒数是一样的，初中的孩子都会证啦，设辅助元用相似就行。
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
double a,b,c;
double check(double x){
double l=sqrt(a*a-x*x);
double r=sqrt(b*b-x*x);
return l*r/(l+r);
}
int main(){
cin>>a>>b>>c;
double l=0,r=min(a,b);
while(r-l>=1e-5){
double mid=(l+r)/2;
if(check(mid)>c)l=mid;
else r=mid;
}
printf("%.3lf
",r);
}