– 有一个由按钮组成的矩阵, 其中每行有6个按钮, 共5行
– 每个按钮的位置上有一盏灯
– 当按下一个按钮后, 该按钮以及周围位置(上边, 下边, 左边, 右边)的灯都会改变状态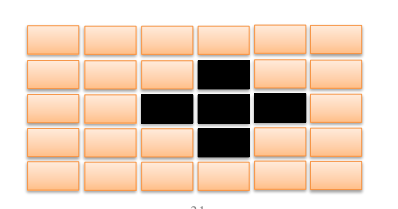
– 如果灯原来是点亮的, 就会被熄灭
– 如果灯原来是熄灭的, 则会被点亮
• 在矩阵角上的按钮改变3盏灯的状态
• 在矩阵边上的按钮改变4盏灯的状态
• 其他的按钮改变5盏灯的状态

与一盏灯毗邻的多个按钮被按下时,一个操作会抵消另一次操作的结果
给定矩阵中每盏灯的初始状态,求一种按按钮方案,使得所有的灯都熄灭
输入:
– 第一行是一个正整数N, 表示需要解决的案例数
– 每个案例由5行组成, 每一行包括6个数字
– 这些数字以空格隔开, 可以是0或1
– 0 表示灯的初始状态是熄灭的
– 1 表示灯的初始状态是点亮的
输出:
– 对每个案例, 首先输出一行,
输出字符串 “PUZZLE #m”, 其中m是该案例的序
号
– 接着按照该案例的输入格式输出5行
• 1 表示需要把对应的按钮按下
• 0 表示不需要按对应的按钮
• 每个数字以一个空格隔开
测试样例:
输入:
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
输出:
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
解题思路:
第2次按下同一个按钮时,
将抵消第1次按下时所产生的结果
第2次按下同一个按钮时,
将抵消第1次按下时所产生的结果
每个按钮最多只需要按下一次
• 第2次按下同一个按钮时,
将抵消第1次按下时所产生的结果
每个按钮最多只需要按下一次
• 各个按钮被按下的顺序对最终的结果没有影响
• 第2次按下同一个按钮时,
将抵消第1次按下时所产生的结果
每个按钮最多只需要按下一次
• 各个按钮被按下的顺序对最终的结果没有影响
• 对第1行中每盏点亮的灯, 按下第2行对应的按钮, 就可以熄灭第1行的全部灯
• 如此重复下去, 可以熄灭第1, 2, 3, 4行的全部灯
经过观察, 发现第1行就是这样的一个 “局部”
– 因为第1行的各开关状态确定的情况下, 这些开关作用过后, 将导致第1行某些灯是亮的, 某些灯是灭的
要熄灭第1行某个亮着的灯(假设位于第i列), 那么唯一的办法就是按下第2行第i列的开关
(因为第1行的开关已经用过了, 而第3行及其后的开关不会影响到第1行)
– 为了使第1行的灯全部熄灭, 第2行的合理开关状态就是唯一的• 第2行的开关起作用后,为了熄灭第2行的灯, 第3行的合理开关状态就也是唯一的
以此类推, 最后一行的开关状态也是唯一的
• 只要第1行的状态定下来, 记作A, 那么剩余行的情况就是确定唯一的了
推算出最后一行的开关状态, 然后看看最后一行的开关起作用后,最后一行的所有灯是否都熄灭:
• 如果是, 那么A就是一个解的状态
• 如果不是, 那么A不是解的状态, 第1行换个状态重新试试
• 只需枚举第1行的状态, 状态数是2的6次方 = 64
关键记住这点:当前行灯的状态是下一行的按钮按下的方案,因为下一行按此方案,才能保证当前行的灯都熄灭。
此测试数据:
输入灯的第1组测试数据
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
需要逐行输入,后续再进行优化,稍微有点麻烦,抱歉了!大家也可以自己优化。
python代码如下:

1 #print("{0:b}".format(3)) 2 #print(bin(5).replace('0b','')) 3 #print(int("011010",2)) 26 4 #print(int("100111",2)) 39 5 #print(int("001001",2)) 9 6 #print(int("100101",2)) 37 7 #print(int("011100",2)) 28 8 #print(int("101001",2)) 41 9 #print(int("110101",2)) 53 10 #print(int("100111",2)) 39 11 #print(bin(5)) 12 #print(type(bin(5).replace('0b',''))) 13 #print(int(bin(5).replace('0b',''))>>2) 14 #print(bin(5)) 15 #print(39 ^ (1 << 1)) 16 #print(bin(39^(1<<1))) 17 #print(bin(4)) 18 #print((5 >> 2) & 0) 19 #m = "00220202020202020222000200" 20 #print(''.join(["%s " % i for i in m])) 21 """ 22 输入灯的第1组测试数据 23 0 1 1 0 1 0 24 1 0 0 1 1 1 25 0 0 1 0 0 1 26 1 0 0 1 0 1 27 0 1 1 1 0 0 28 29 输出按灯的方案 30 1 0 1 0 0 1 31 1 1 0 1 0 1 32 0 0 1 0 1 1 33 1 0 0 1 0 0 34 0 1 0 0 0 0 35 36 输入灯的第2组测试数据 37 0 0 1 0 1 0 38 1 0 1 0 1 1 39 0 0 1 0 1 1 40 1 0 1 1 0 0 41 0 1 0 1 0 0 42 43 输出按灯的方案: 44 1 0 0 1 1 1 45 1 1 0 0 0 0 46 0 0 0 1 0 0 47 1 1 0 1 0 1 48 1 0 1 1 0 1 49 """ 50 51 oriLight = [0 for i in range(0,5)] #输入灯的矩阵,一个比特表示一盏灯,初始化为[0,0,0,0,0]这样的List 52 lights = [0 for i in range(0,5)] #不停变化的灯矩阵 53 result = [0 for i in range(0,5)] #结果开关矩阵 54 switchs=0 #某一行的开关状态 55 56 #定义读入命令行输入数据的函数 57 def ReadInitData(): 58 i = 0 59 print("请输入每盏灯的初始数据,每盏灯空格间隔:") 60 while (i < 5): 61 line = input() 62 oriLight[i] = int(line.replace(" ", ""), 2) 63 i = i + 1 64 65 #获取输入值转化为二进制,然后去第ilocation位置的值 66 def GetBit(iData,ilocation): 67 #print(iData>>ilocation) 68 rtn = (iData >> ilocation) & 1 69 return rtn 70 71 def Flip(iData,ilocation): 72 iData = iData ^ (1 << ilocation) 73 return iData 74 75 def OutPutResult(list): 76 print("所有灯都熄灭的按下方案为: ") 77 for i in list: 78 #首先整数转二进制,然后去除0b开头的字符,最后zfill函数,保证6个长度,不够,前面补0 79 tempStr = bin(i).replace('0b','').zfill(6) 80 #遍历,给每个字符串中的字符增加空格 81 print("".join(["%s " % t for t in tempStr])) 82 #for t in tempStr: 83 #print(t,end=" ") 84 #print("") 85 def main(): 86 87 #读取输入灯的初始数据,然后存入oriLight列表中 88 ReadInitData() 89 #遍历首行开关的64种状态,每个整型值的二进制值代表第一行其中一组按下方案 90 n = 0 91 while (n<64): 92 # 每次循环前,都把输入灯的初始数据重新给变化的lights赋值 93 #lights = oriLight这里提醒大家不要这样写,如果这样写了,lights的变化会影响oriLight的变化,它们指向同一块地址 94 #这里使用的是浅拷贝copy.copy(a),为了更加保险,也可以使用深拷贝copy.deepcopy(a) 95 lights = oriLight[:] 96 #遍历针对第一行的64种变化方案给swiths赋值 97 switchs = n 98 for i in range(5): 99 result[i] = switchs; #第i行的开关方案 100 for j in range(6): 101 #如果switchs二进制中,值是1的表示按下,需要处理周围几盏灯的状态,如果值是0,则不处理 102 if (GetBit(switchs,j)) : 103 #首先修改按下按钮本身自己灯的状态 104 lights[i] = Flip(lights[i], j); 105 #j表示列,如果是小于第5列,才需要修改按下按钮左边的灯状态,从右往左方向,第0列在最右边 106 if j < 5 : 107 lights[i] = Flip(lights[i], j + 1) #改左灯的状态 108 # j表示列,如果是大于第0列,才需要修改按下按钮右边的灯状态 109 if j > 0 : 110 lights[i] = Flip(lights[i],j - 1) #修改右灯的状态 111 112 if (i < 4): 113 # 通过异或运算符,修改按下按钮的下面方向的按钮灯的状态,1^0,值1灯亮,1^1,值0灯熄灭 114 lights[i + 1] ^= switchs 115 # 第i行灯情况确定第i + 1行开关方案,因为我们需要把第i行亮的灯都熄灭,那么i+1行的哪些按钮按下的方案就确定下来了 116 switchs = lights[i] 117 118 #假设成立,说明第5行的灯都灭了,然后输出该按钮按下方案 119 if (lights[4] == 0): 120 OutPutResult(result) 121 #print(n) 122 break 123 n += 1 124 125 if __name__=="__main__": 126 main()
