20182307 2019-2020-1 《数据结构与面向对象程序设计》第八周学习总结
目录
教材学习内容总结
第13章 查找与排序 主要介绍了查找和排序的概念,通过举出不同的例子来具体说明。查找部分以线性查找和二分查找为例,比较了二者的优劣与各自特性;排序部分以选择排序、插入排序、冒泡排序、快速排序、归并排序为例,详细介绍了每一种排序方法的思想与运作机制,比较了各算法之间的时间复杂度。
学习笔记:
- 查找
- 查找是指在一组数据项中找到指定的目标元素
- 线性查找
- 扫描整个表,依次将每个值与目标元素进行比较,退出情况为找到目标或扫描至表尾。

- 二分查找
- 首先,二分查找可应用的数据项必须是有序的
- 每次查找从中间开始,每次与所选值进行比较后可以减少查找池中一半的元素。
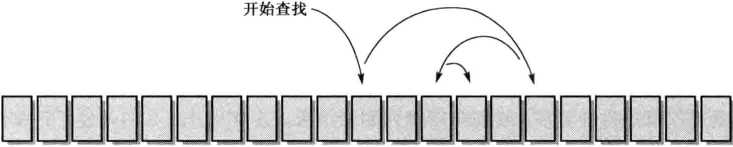
- 比较分析:一般情况下,二分查找比线性查找更有效,但二分查找只可应用于有序的表。
- 排序
- 排序是按某种标准将一列数据项按确定的次序重排的过程
- 选择排序
- 扫描整个表,分别将每个值放到排好序的最终位置,从而完成一组值的排序
- 循环中的判断语句条件的更改,可决定排序的形式:升序或降序
- 插入排序
- 重复地将一个具体的值插入到表中已有序的子序列中
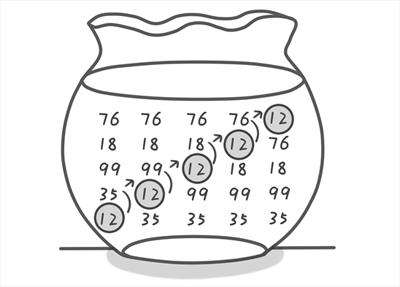
- 冒泡排序
- 扫描整个表,重复地比较表中的相邻元素,如果呈逆序就交换
- 快速排序
- 先选择表中的一个元素作为划分元素,小于划分元素的所有元素放到划分元素左侧,大于划分元素的所有元素放到它的右侧
- 当扫描过程在划分点相遇时,划分完成
- 归并排序
- 归并排序递归地将表平分为两部分,直到每个子表中只含有一个元素,然后将这些子表归并为有序表,从而完成排序
- 比较分析:选择排序、插入排序、冒泡排序都有着相近的效率,时间复杂度皆为O(n^2),但是插入排序的最优情形依赖于初始数据的情况,可以为O(n)。
教材学习中的问题和解决过程
- 问题1:快速排序的稳定性?
- 个人理解:算法的稳定性,主要考虑的是元素在排序之后次序是否发生变化,这种情况一般发生在遇到相同元素时。例如数列3 3 4 9,标记第一个3为3,如果采用某种排序后3的位置排在了3后,则称这个算法是不稳定的。快速排序时就需要考虑这样的问题,即遇到相同元素时是否需要进行交换,交换就可能导致不稳定,因为次序改变了,所以快速排序并不是一个稳定的算法。
- 问题2:如何更好的理解快速排序的过程?
- 网上资料:快速排序|菜鸟教程
- 个人理解:一个方便简洁的理解方式是“挖坑填坑”思想。比如取表中第一项为划分元素,就认为取出后第一位的位置空缺了,需要别的元素进行填补。因为遵从从小到大的排序方式,从表尾往前扫描,第一个比划分元素小的填入空缺,此时又可以认为该元素的位置空缺了,需要填补,以此类推,直到最后一个元素填入了合适的位置,再将最开始时取出的首位元素即划分元素填入。

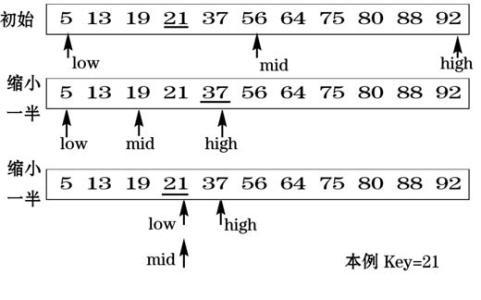
- 问题3:递归实现二分查找时怎么确定基本情形?
- 书本内容:二分查找每次比较都将可行候选者的范围缩小一半,直到最后找到目标元素。
- 个人理解:二分查找的基本思路是先从一个有序表的中间开始,如果目标大于此中间数,就从表中后一半的数据中开始查找,以此类推。所以若要让递归的二分查找成功运行到基本情形,中间数的记录是至关重要的。如果中间数最终与查找范围的最大或最小重合,则达成基本情形,结束递归。
代码调试中的问题和解决过程
- 问题1:二分查找时,无法处理查找池中数据项为偶数数量的情况
- 原因分析:二分查找的特点是从中间开始,但偶数的中间数是两个,所以需要在算法中添加对于中间数的定义,比如向下取整的方式。
- 解决方案:添加
mid = (min+max)以定义中间数 
- 问题2:线性探查法消除冲突情况时,列表中的10和79无法存入

- 原因分析:消除冲突的循环算法中,
j=i+1代码会在i走到过大的值后,导致跳过了可储存的空位。比如空位在第10位,但j过早的加到了11,这样就无法将数存储入空位了 - 解决方案:让j从较小的、固定的常量2开始循环
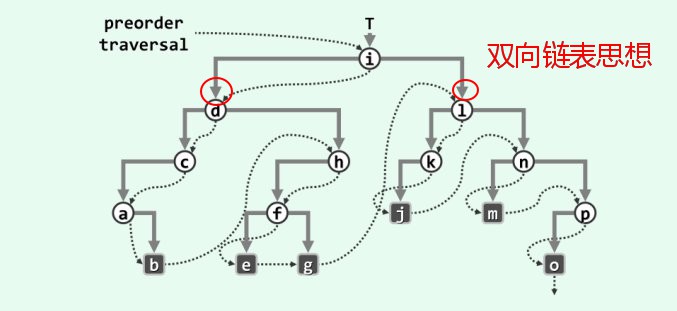
- 问题3:编写二叉排序树代码时遇到了困难
- 原因分析:由于二叉树的特点是,一个根结点下会有两个分支,所以编程时需要引入双向链表的思想。且结点的插入是分次进行的,递归的思想在程序中也会有所体现。
- 网上资料:排序算法Java实现(三):二叉树排序(递归)
代码托管

上周考试错题总结
上周无考试
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 209/209 | 2/2 | 9/9 | |
| 第二、三周 | 290/499 | 2/4 | 18/28 | |
| 第四周 | 516/1015 | 2/6 | 22/50 | |
| 第五周 | 2981/3996 | 2/8 | 32/82 | |
| 第六周 | 1498/5494 | 2/10 | 20/102 | |
| 第七周 | 1519/7013 | 2/12 | 51/153 | |
| 第八周 | 1641/8654 | 2/14 | 21/174 |