最小生成树kruskal 知识点讲解+模板

0.前言

因为本人太蒟了 

我现在连NOIP的初赛都在胆战心惊 并且我甚至连最小生成树都没有学过 

所以这一篇博客一定是最详细的QAQ 哈哈

请您认真看完如果有疏漏之处敬请留言指正 感谢！

Thanks♪(･ω･)ﾉ

1.最小生成树概念

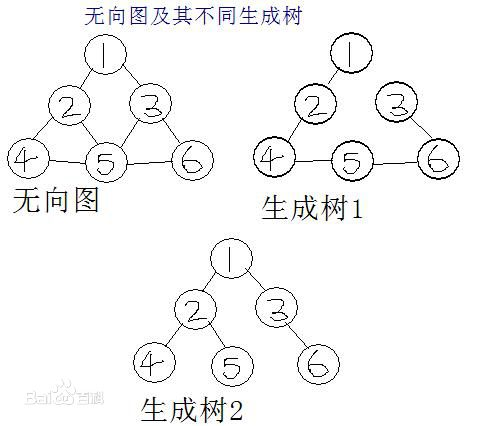
最小生成树到底是什么呢？满脸疑惑

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边

　　　　　　　　　　　　　　　　　　　　　——源自百度百科

　

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得

的 w(T) 最小，则此 T 为 G 的最小生成树。

最小生成树其实是最小权重生成树的简称。

 

 那么我们就明白了

所谓的最小生成树 也不是那么难

最小生成树就是在一个无向图上 选取出边的权值和最小的一棵子树，并且包含所有的节点！

这样我们就非常开心♪(^∇^*)地完成了定义的理解！

打卡通关！(*^▽^*)

2.kruskal算法讲解及模板

接下来我们来讲解一下如何实现上面的最小生成树吧

这里就要引出我们的kruskal

克鲁斯卡尔算法的核心思想是：在带权连通图中，不断地在边集合中找到最小的边，如果该边满足得到最小生成树的条件，就将其构造，直到最后得到一颗最小生成树。

克鲁斯卡尔算法的执行步骤：
第一步：在带权连通图中，将边的权值排序；
第二步：判断是否需要选择这条边（此时图中的边已按权值从小到大排好序）。判断的依据是边的两个顶点是否已连通，如果连通则继续下一条；如果不连通，那么就选择使其连通。
第三步：循环第二步，直到图中所有的顶点都在同一个连通分量中，即得到最小生成树。

 看起来这就非常的简单啦

模板如下（本人艰辛整理）

#include<bits/stdc++.h>
using namespace std;
struct Edge{int u,v,w;}edge[200005];
int fa[5005],n,m,ans,eu,ev,cnt;
inline bool cmp(Edge a,Edge b){ return a.w<b.w; }//快排的依据
inline int find(int x){
    while(x!=fa[x]) x=fa[x]=fa[fa[x]];
    return x;
}//并查集模板，用while循环比递归版快
inline void kruskal(){
   
   
    sort(edge,edge+m,cmp);//将边的权值排序
   
    for(int i=0;i<m;i++){
   
        eu=find(edge[i].u), ev=find(edge[i].v);
        if(eu==ev) continue;//若出现环，则continue
        ans+=edge[i].w;//更新答案
        fa[ev]=eu; cnt++;
        if(cnt==n-1) break;//循环结束条件
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集
    for(int i=0;i<m;i++)
        scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w);
    kruskal();
    printf("%d",ans);
    return 0;
}

3.后记

看完之后是否还有什么问题呢？

其实只要仔细想一想 再结合资料、代码和示意图看一看 就很容易理解

还是点个赞 关注一下下再走吧~ 感谢咯Thanks♪(･ω･)ﾉ