一、树
Vector和List都有明显的弱点,都无法兼顾动态和静态操作的高效性。

Tree可以认为将Vector和List的优点结合了起来,可以认为是列表的列表List<List>,半线性结构。
应用
层次关系的表示
从数学上看,树是一类特殊的图,联通无环图。
树由一组顶点(vertex)以及连接于期间的若干条边(edge)组成。
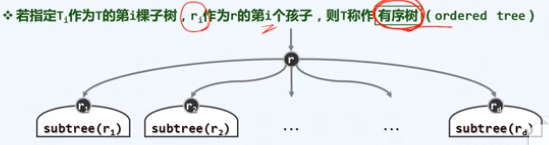
在计算机科学中,会指定某个特定的顶点,称之为根(root)
在指定了根之后,我们称该树为有根树(rooted tree)
从程序实现的角度,我更多地将顶点(vertex)称作节点(node)
通过彼此嵌套,小型的有根树可以变成大型的有根树
对于任何一组有根树,可以通过引入新的顶点,在新的顶点和此前各有根树的树根之间引入对应的一条连边,从而构成规模更大的一棵有根树。
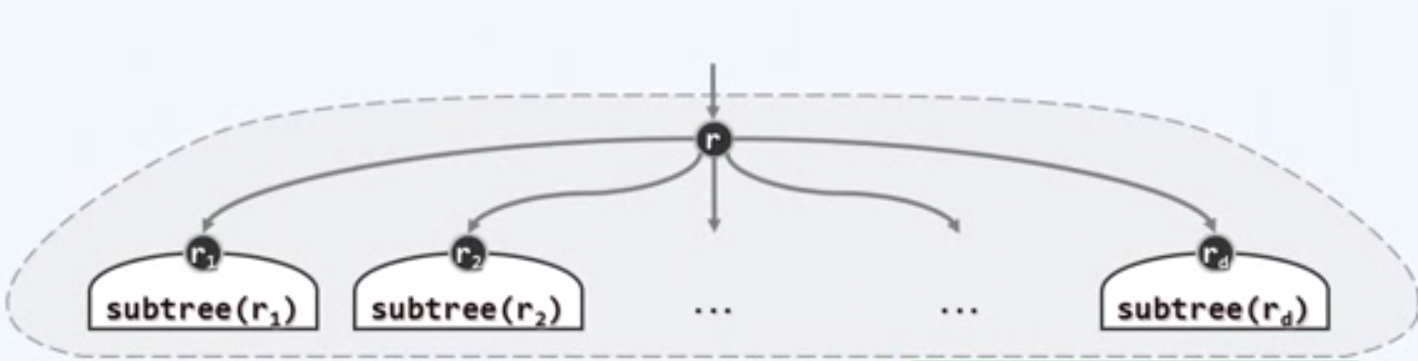


ri称作r的孩子(child),ri之间互称兄弟(sibling),r为其父亲(parent)
d=degree(r)为r的(出)度(degree)
某一节点v孩子的总数,称作该节点的度数或度(degree),无孩子的节点称为叶节点(leaf node),包括根在内的其余节点皆为内部节点(internal node)。
n为顶点数,e为边数,

任何一棵树所含的边数,恰好等于所有顶点的度数之和,也等于顶点总数减1,一棵树的边数与顶点数目是同阶的。

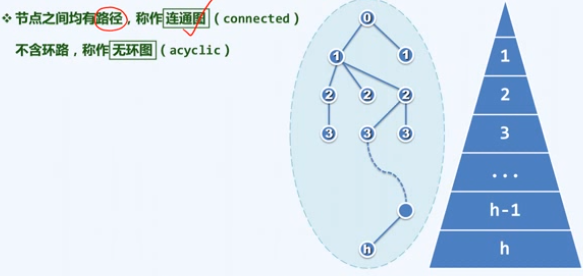
树是
无环连通图
极小连通图
极大无环图
任一节点v与根之间存在唯一路径,path(v, r) = path(v)
因此,每一节点也有了一个唯一的指标,即该节点到根的那条路径的长度
一旦指定了根,其他节点都会获得该确定的指标
每个节点v到根r的唯一路径所经过边的数目,称作v的深度(depth),记作depth(v)
约定根节点的深度,即depth(r)=0,故属于第0层
不致歧义时,路径、节点和子树可相互指代
path(v)上节点,均为v的祖先(ancestor),v是它们的后代(descendent)
除自身以外,是真(proper)祖先/后代
根节点是所有节点的公共祖先
半线性:在任一深度,v的祖先/后代若存在,则必然/未必唯一
即节点有唯一祖先,但并不一定有唯一后代,前驱的唯一性有保证,后继的唯一性没有保证
没有祖先的节点是根节点,没有后代的节点是叶节点
所有叶子深度中的最大者称作(子)树(根)的高度
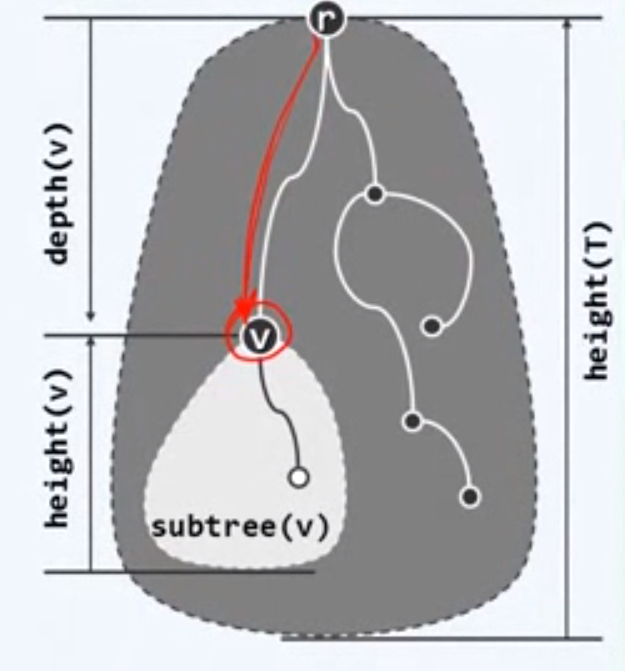
空树的高度取作-1
depth(v)+height(v)<=height(T)
二、树的表述
接口
| 节点 | 功能 |
| root() | 根节点 |
| parent() | 父节点 |
| firstChild() | 长子 |
| nextSibling() | 兄弟 |
| insert(i, e) | 将e作为第i各孩子插入 |
| remove(i) | 删除第i各孩子(及其后代) |
| traverse() | 遍历 |
树的表示
观察:除根外,任一节点有且仅有一个父节点
构思:将节点组织为序列,各节点分别记录
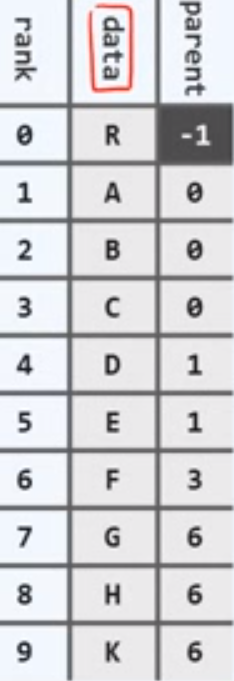
data 本身信息
parent 父节点的秩或位置


将所有节点汇聚为一个序列,不同的是为每个节点准备一个名为children的引用,该引用指向的是所有的孩子构成的小的数据集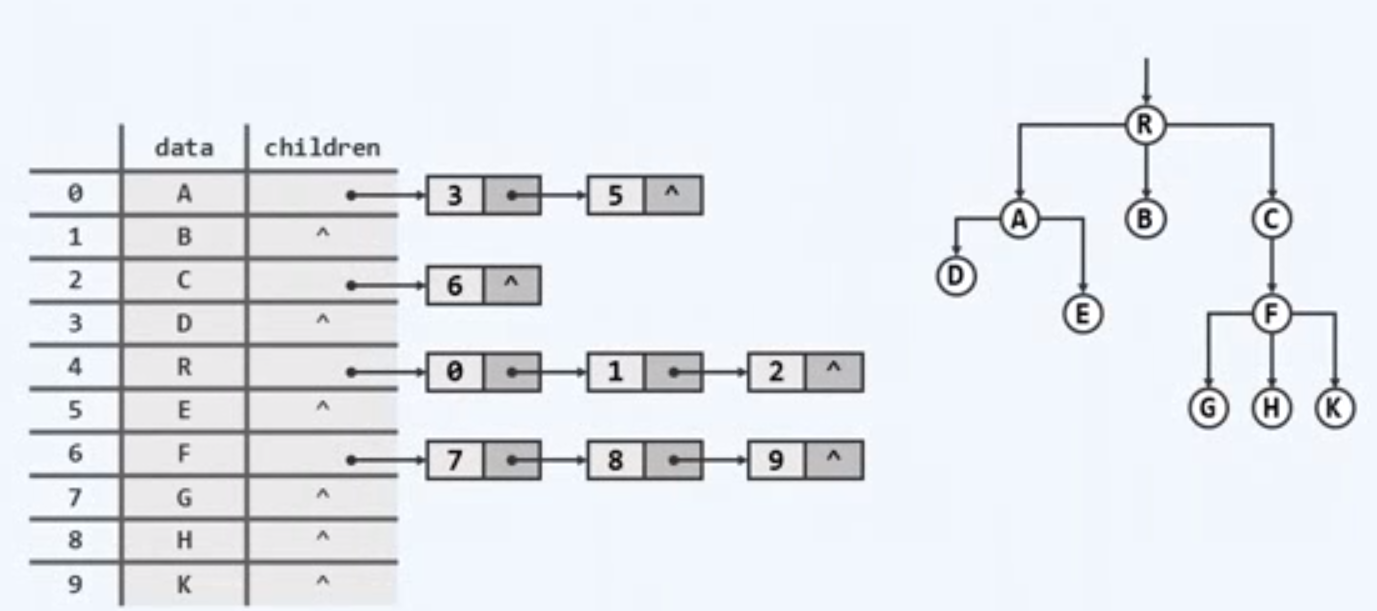
向上查找的优势丧失,不得不遍历整个线性序列
将上面两个线性序列结合起来
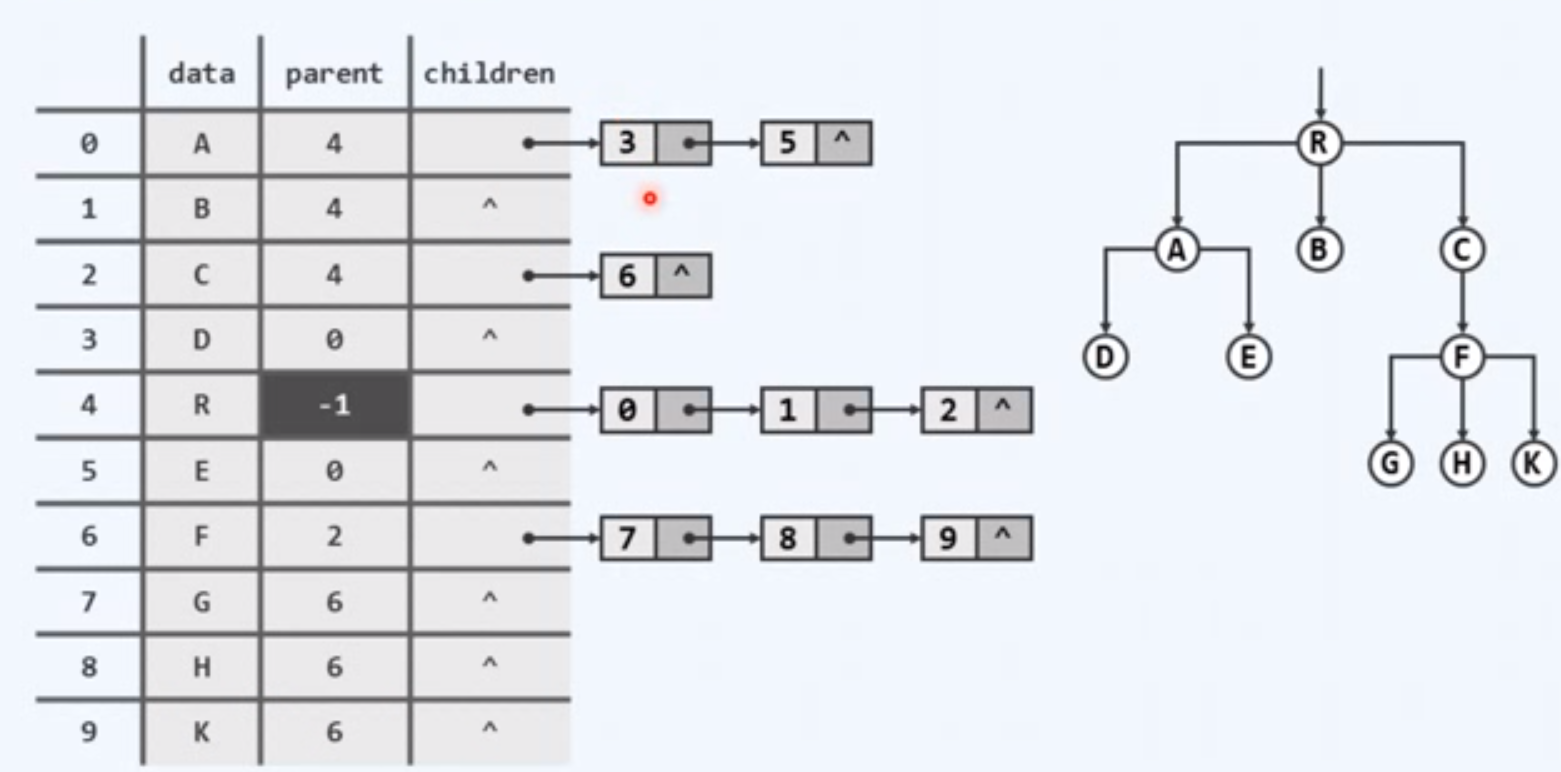
仍然存在不足,children数据集在规模上可能十分悬殊
长子+兄弟
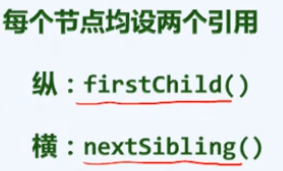
三、二叉树概述
二叉树虽然是树的子集,但施加了某些条件之后,二叉树可以代表所有的树
节点度数不超过2的树,称作二叉树(binary tree)
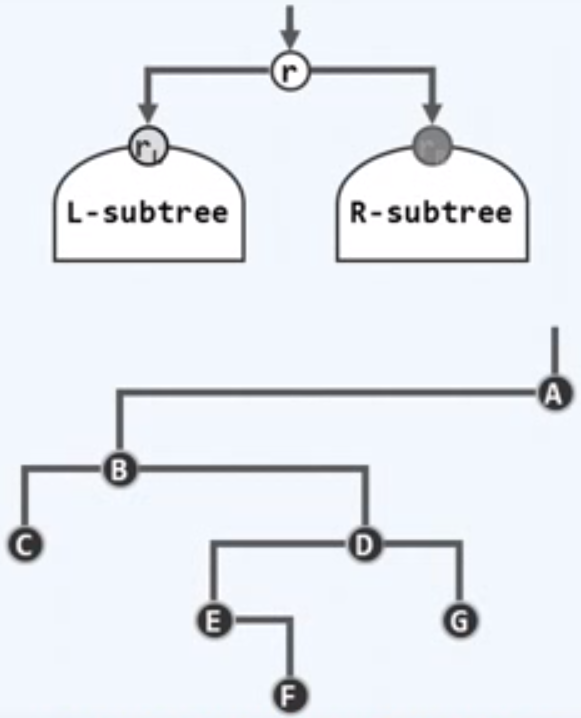
同一节点的孩子和子树,均以左右区分,

隐含有序,左在先,右在后
基数
深度为k的节点,至多2k个


满树:
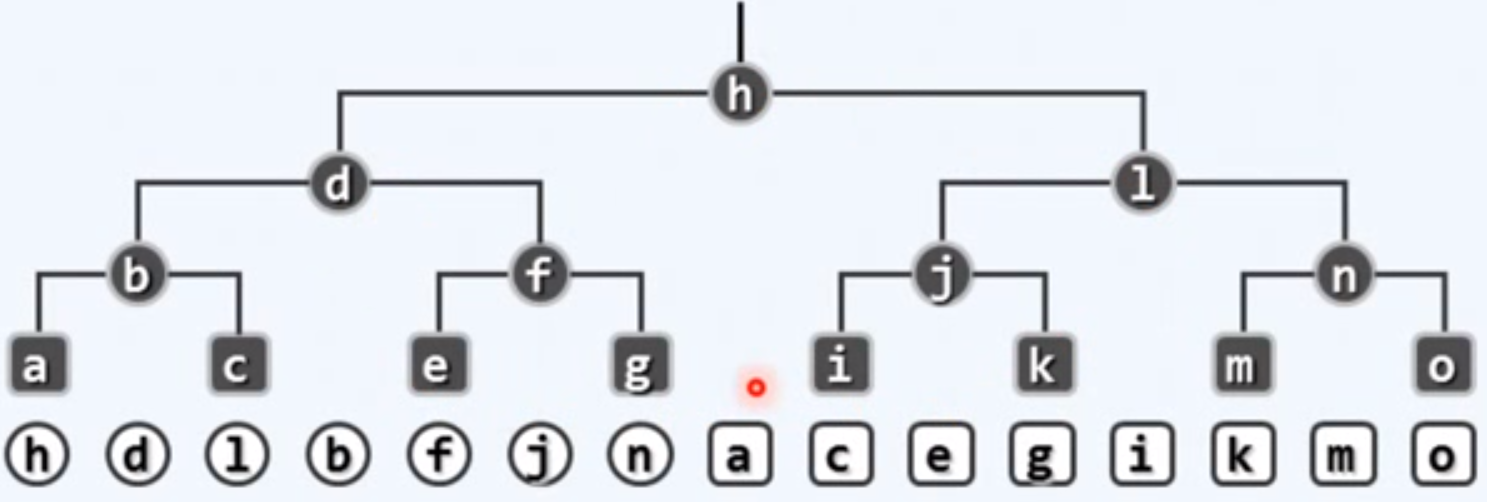
二叉树在横向上的宽度与纵向上的高度呈指数的关系,宽度是高度的指数
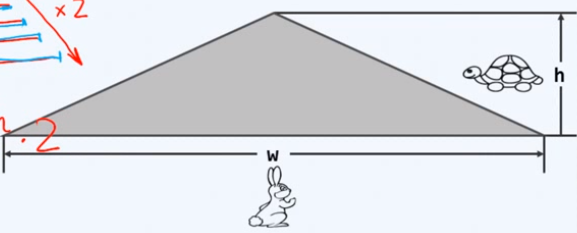
二叉搜索树的基础
把出度记在二叉树上
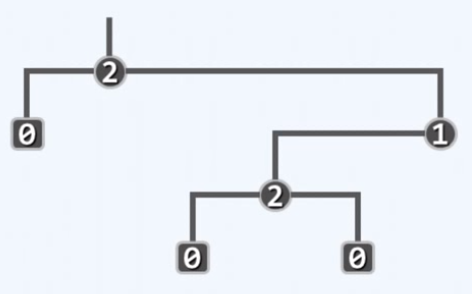
真二叉树,每个节点的出度都是偶数或者零
可以假想为每个节点添加足够多的孩子节点,算法就可更简单实现
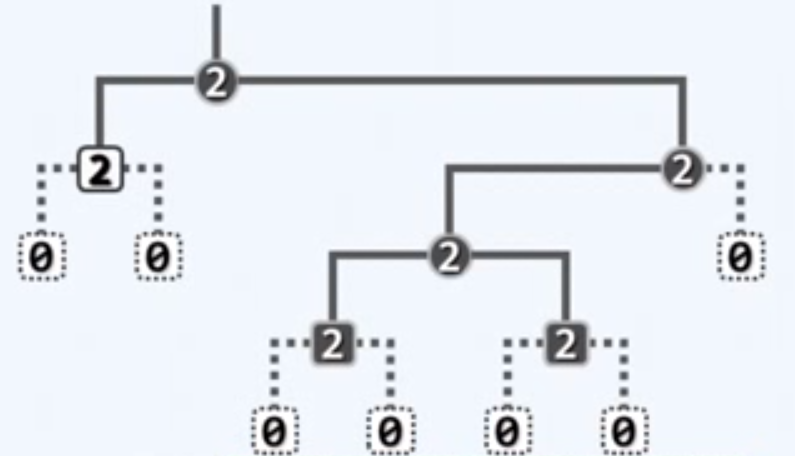
描述多叉树
二叉树是多叉树的特例,但在有根且有序时,其描述能力足以覆盖后者
多叉树可以转化并表示为二叉树,回忆长子-兄弟表示法...

四、二叉树实现
BinNode模板

#define BinNode(T) BinNode<T> //节点位置 template <typename T> struct BinNode { BinNodePosi(T) parent, lChild, rChild; // 父亲,孩子 T data; int height; int size(); // 高度,子树规模 BinNodePosi(T) insertAslC(T const &); // 作为左孩子插入新节点 BinNodePosi(T) insertAsRC(T const &); // 作为右孩子插入新节点 BinNodePosi(T) succ(); // (中序遍历意义下)当前节点的直接后继 template <typename VST> void travLevel(VST &); // 子树层次遍历 template <typename VST> void travPre(VST &); // 子树先序遍历 template <typename VST> void travIn(VST &); // 子树中序遍历 template <typename VST> void travPost(VST &); // 子树后序遍历 };

接口实现
template <typename T> class BinTree { protected: int _size; // 规模 BinNodePosi(T) _root; // 根节点 virtual int updateHeight(BinNodePosi(T) x); // 更新节点x的高度 void updateHeightAbove(BinNodePosi(T) x); // 更新x及其祖先的高度 public: int size() const { return _size; } // 规模 bool empty() const { return !_root; } // 判空 BinNodePosi(T) root() const { return _root; } // 树根 /* 子树接入,删除和分离接口 */ /* 遍历接口 */ };
高度更新
只有单个节点,不存在任何节点的树(空树),正常情况如何统一?
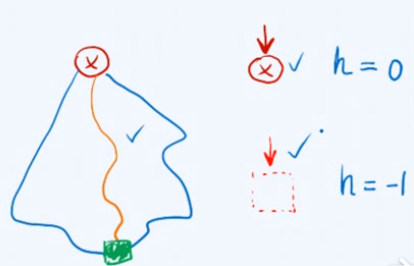
通过宏定义封装,重新命名等价意义上的高度,
#define stature(p)((p)? (p)->height :-1) // 节点高度--约定空树高度为-1
节点的高度之所以会发生变化,是因为左孩子或是右孩子的高度发生了变化
一个节点的高度等于其左孩子或右孩子高度的最大者,再加1
template <typename T> //更新节点x高度,具体规则因树不同而异 int BinTree<T>::updateHeight(BinNodePosi(T) x) { return x->height = 1 + max(stature(x->lChild), stature(x->rChild)); } // 此处采用常规二叉树规则,0(1)
节点插入

template <typename T> BinNodePosi(T) BinTree<T>::insertAsRC(BinNodePosi(T) x, T const & e) { // insertAsLC()对称 _size++; x->insertAsRC(e); // x祖先的高度可能增加,其余节点比如不变 updateHeightAbove(x); return x->rChild; }
五、先序遍历
按照某种次序,访问树中各节点,每个节点被访问恰好一次

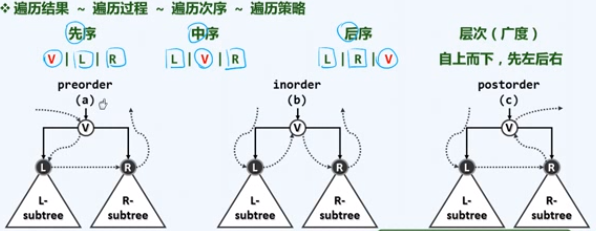
递归
template <typename T, typename VST> void traverse(BinNodePosi(T) x, VST & visit) { if (!x) return; visit(x->data); traverse(x->lChild, visit); traverse(x->rChild, visit); } // T(n) =0(1) + T(a) + T(n-a-1) = O(n)
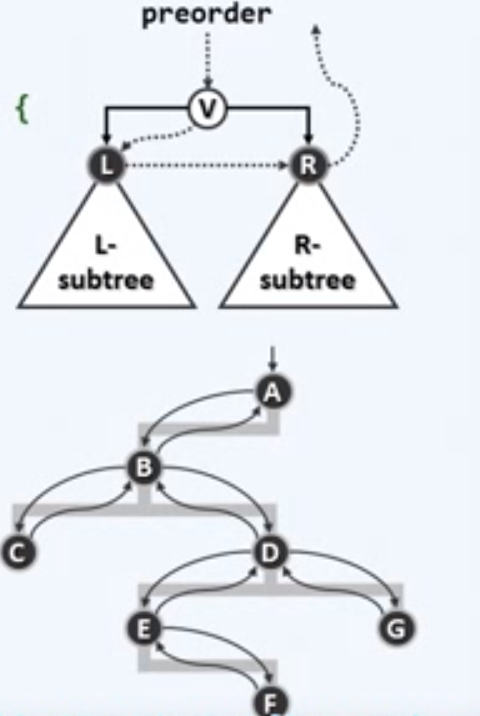
迭代1:实现
引入栈
template <typename T, typename VST> void travPre_I1(BinNodePosi(T) x, VST & visit) { Stack <BinNodePosi(T)> S; // 辅助栈 if (x) S.push(x); // 根节点入栈 // 在栈变空之前反复循环 while (!S.empty() { x = S.pop(); visit(x->data); // 弹出并访问当前节点 if (HasRchild(*x)) S.push(x->rChild); // 右孩子先入后出 if (HasLChild(*x)) S.push(x->lChild); // 左孩子后入先出 } // 体会以上两句的次序 }
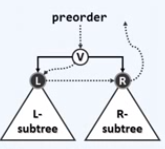
先父,后左孩子,再右孩子
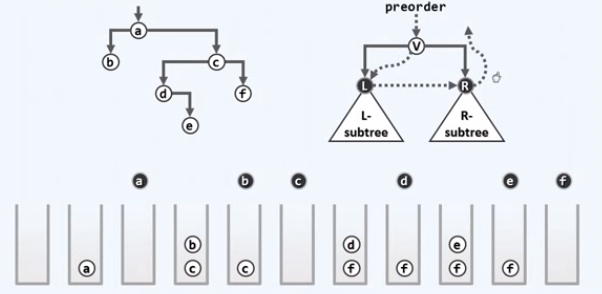
迭代2:思路
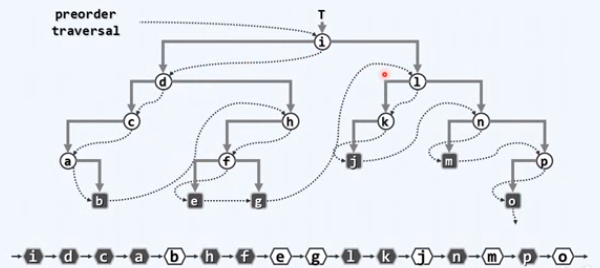
总是沿着左侧分支下行的链叫当前子树的左侧链
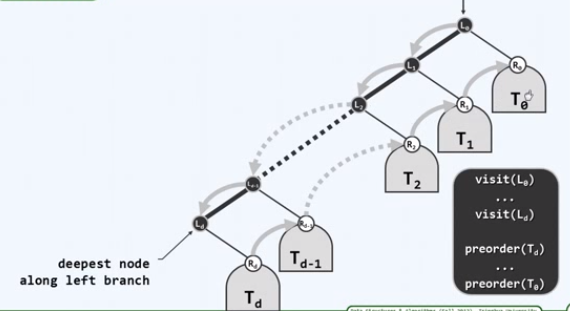
迭代2:实现
template <typename T, typename VST> static void visitAlongLeftBranch( BinNodePosi(T) x, VST & visit, Stack <BinNodePosi(T)> & S ) { while (x){ // 反复地 visit(x->data); // 访问当前节点 S.push(x->rChild); // 右孩子(右子树)入栈(将来逆序出栈) x = x->lChild; // 沿左侧链下行 } // 只有右孩子、Null可能入栈--增加判断以剔除后者,是否值得? }
左算法
template <typename T, typename VST> void travPre_I2(BinNodePosi(T) x, VST & visit) { stack <BinNodePosi(T)> S; // 辅助栈 while (true) { // 以(右)子树为单位,逐批访问节点 visitAlongLeftBranch(x, visit, S); // 访问子树x的左侧链,右子树入栈缓冲 if (S.empty()) break; // 栈空即推出 x = S.pop(); // 弹出下一子树的根 } // #pop = #push =#visit = O(n) = 分摊O(1) }
迭代2:实例
^是空

六、中序遍历
递归
template <typename T, typename VST> void traverse(BinNodePosi(T) x, VST & visit) { if (!x) return; traverse(x->lChild, visit); visit(x->data); traverse(x->rChild, visit); } // T(n) =0(1) + T(a) + T(n-a-1) = O(n)
观察

没有左孩子相当于左孩子被访问过了
思路
访问左侧链节点,遍历右子树
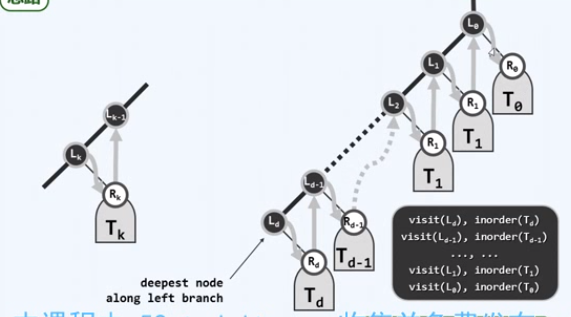
实现
template <typename T> static void goAlongLeftBranch(BinNodePosi(T) x, Stack <BinNodePosi(T)> & S) { while (x) { S.push(x); x = x->lChild; } // 反复入栈,沿左侧分支深入 }
左算法
template<typename T, typename V> void travIn_I1(BinNodePosi(T) x, V& visit) { Stack <BinNodePosi(T)> S; // 辅助栈 while (true) // 反复地 { goAlongLeftBranch(x, S); // 从当前节点触发,逐批入栈 if (S.empty()) break; // 直至所有节点处理完毕 x = S.pop(); // x的左子树或为空,或已遍历(等效于空),故可以 visit(x->data); // 立即访问之 x = x->rChild; // 再转向其右子树(可能为空,留意处理手法) } }
实例
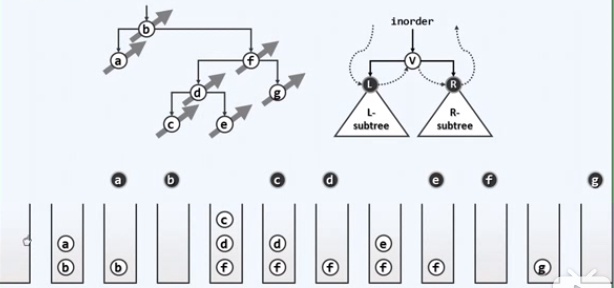
七、层次遍历
在垂直方向按深度将所有节点划分为若干等价类,有根性就是垂直方向的次序,同一深度的节点如何定义次序呢?
可以根据垂直方向和水平方向的次序定义整体的次序,而进行遍历
具体说,自高向低,在每一层自左向右,逐一访问树中的每一节点,层次遍历
前面的策略都有后代先于祖先访问的情况,即逆序,无论隐式的还是显式的都需要借助栈结构
而在层次遍历中,所有节点都严格按照深度次序,由高到低的接收访问,严格满足顺序性
队列大显身手
实现
template <typename T> template <typename VST> void BinNode<T>::travLevel(VST & visit) { // 二叉树层次遍历 Queue<BinNodePosi(T)> Q; // 引入辅助队列 Q.enqueue(this); // 根节点入队 while (!Q.empty() { // 在队列再次变空之前,反复迭代 BinNodePosi(T) x = Q.dequeue(); // 取出队首节点,并随即 visit(x->data); // 访问之 if (HasLChild(*x)) Q.enqueue(x->lChild)); // 左孩子入队 if (HasRChild(*x)) Q.enqueue(x->rChild); // 右孩子入队 } }
左先右后
A节点入队,右侧的是现在队列的照片
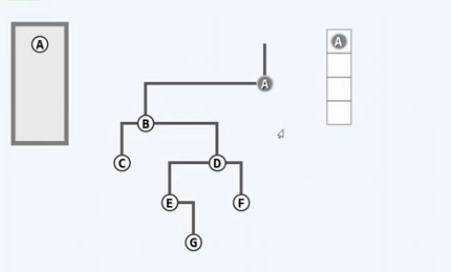
取出队首的节点
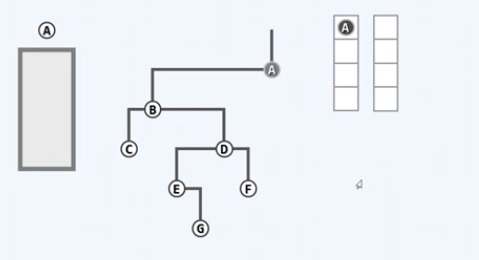
左顾右盼,A只有左孩子B,B入队
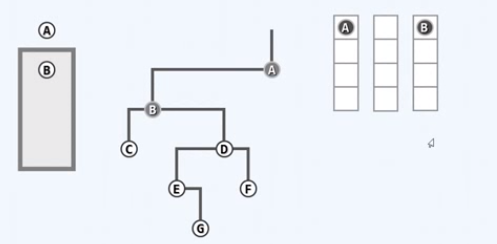
取出队首节点B
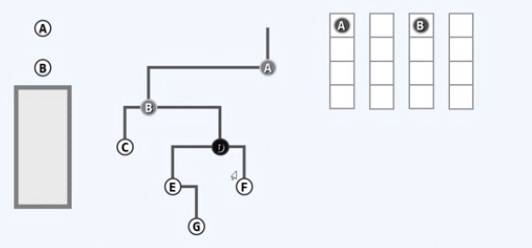
对B进行访问,左顾右盼,左右孩子都有,都要入队,左先右后

取出队首节点C

访问C节点,左顾右盼,都是空的
取出队首节点D

访问D,左顾右盼,左右孩子都有,都要入队
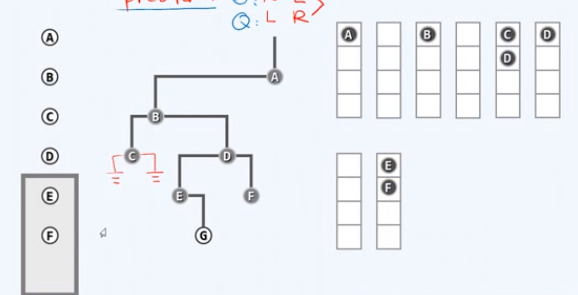
取出队首节点E
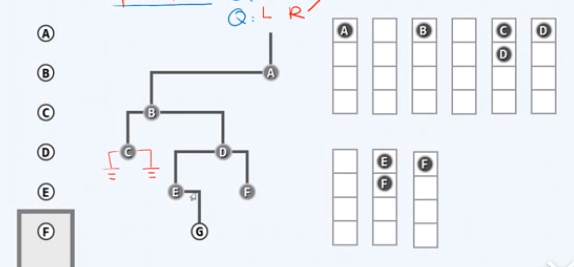
访问E,左顾右盼,发现右孩子G,入队

取出队首元素F
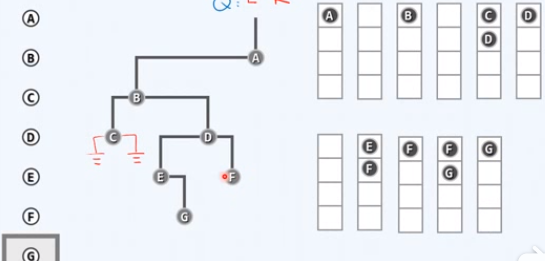
访问F,没有左右孩子,进入下一步迭代
取出队首G,访问G,左顾右盼,没有左右孩子
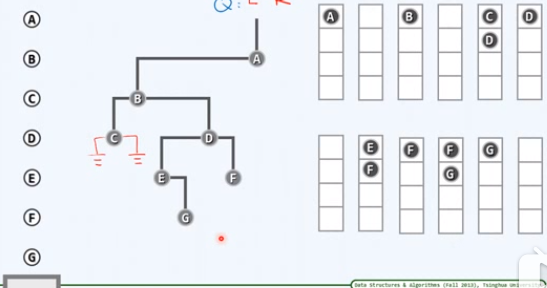
层次遍历完成
八、重构
由任何一棵二叉树,都可以导出三个序列:先序、中序和后序遍历序列
它们都是由树中的所有节点,依照对应的遍历策略所确定的次序,依次排列而成
如果已知某棵树的遍历序列,是否可以忠实还原出树的拓扑结构?
只需要中序遍历序列,和先序、后序中两者中的一个就可以还原树的结构
数学归纳