K-Means

原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12870414.html

K-Means

K-Means 是一种无监督学习，解决的是聚类问题。K 代表的是 K 类，Means 代表的是中心，这个算法的本质是确定 K 类的中心点，当找到了这些中心点，也就完成了聚类。

K-Means 的工作原理：

1. 选取 K 个点作为初始的类中心点，这些点一般都是从数据集中随机抽取的；
2. 将每个点分配到最近的类中心点，这样就形成了 K 个类，然后重新计算每个类的中心点；
3. 重复第二步，直到类不发生变化，或者你也可以设置最大迭代次数，这样即使类中心点发生变化，但是只要达到最大迭代次数就会结束。

sklearn 中的 K-Means 算法

在 K-Means 类创建的过程中，有一些主要的参数：

• n_clusters: 即 K 值，一般需要多试一些 K 值来保证更好的聚类效果。可以随机设置一些 K 值，然后选择聚类效果最好的作为最终的 K 值；
• max_iter： 最大迭代次数，如果聚类很难收敛的话，设置最大迭代次数可以让我们及时得到反馈结果，否则程序运行时间会非常长；
• n_init：初始化中心点的运算次数，默认是 10。程序是否能快速收敛和中心点的选择关系非常大，所以在中心点选择上多花一些时间，来争取整体时间上的快速收敛还是非常值得的。由于每一次中心点都是随机生成的，这样得到的结果就有好有坏，非常不确定，所以要运行 n_init 次, 取其中最好的作为初始的中心点。如果 K 值比较大的时候，可以适当增大 n_init 这个值；
• init： 即初始值选择的方式，默认是采用优化过的 k-means++ 方式，也可以自己指定中心点，或者采用 random 完全随机的方式。自己设置中心点一般是对于个性化的数据进行设置，很少采用。random 的方式则是完全随机的方式，一般推荐采用优化过的 k-means++ 方式；
• algorithm：k-means 的实现算法，有“auto”、 “full”、 “elkan”三种。一般来说建议直接用默认的"auto"。简单说下这三个取值的区别，如果选择"full"采用的是传统的 K-Means 算法，“auto”会根据数据的特点自动选择是选择“full”还是“elkan”。一般选择默认的取值，即“auto” 。

看个具体的例子

准备数据

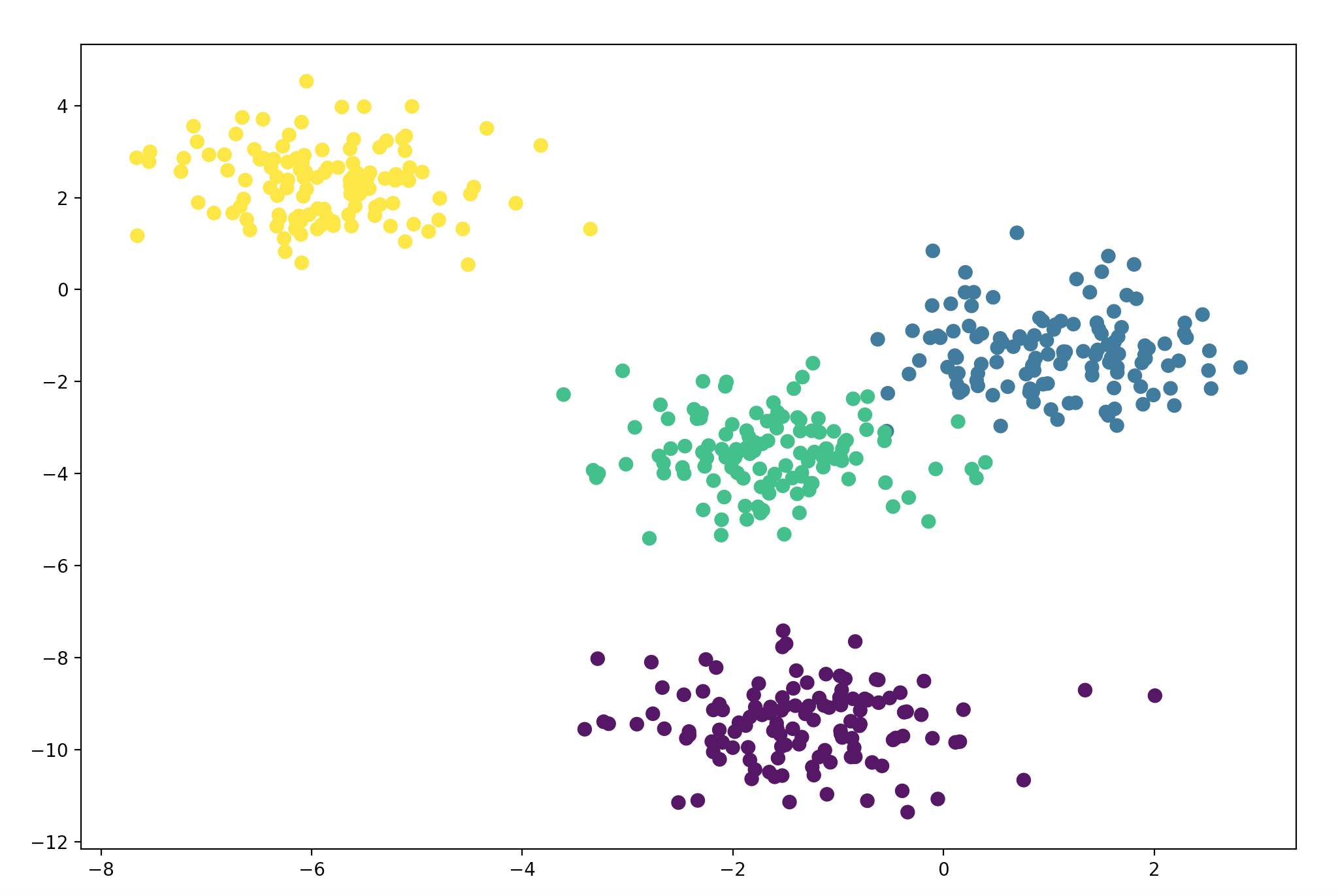
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=500, n_features=2, centers=4, cluster_std=0.8, random_state=2)
# (500, 2)
print(X.shape)

plt.figure(figsize=(12, 8))
plt.scatter(X[:, 0], X[:, 1], s=50, marker='o', c=y)
plt.show()

数据分布图如下：

建模训练

from sklearn.cluster import KMeans

model = KMeans(n_clusters=3)
# KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
#        n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
#        random_state=None, tol=0.0001, verbose=0)
model.fit(X)

# [[-1.34328465 -9.43322827]
#  [-5.87300836  2.30937527]
#  [-0.29807303 -2.45532599]]
print(model.cluster_centers_)

# [0 1 0 2 1 2 2 2 2 2 2 2 2 2 1 2 2 0 1 2 1 0 2 2 0 0 2 2 2 0 0 2 2 2 1 1 2
#  2 2 0 2 1 2 2 1 0 0 0 1 2 0 0 2 2 0 1 2 0 2 2 2 1 1 0 2 2 0 2 0 0 1 2 0 2
#  2 0 2 2 2 0 1 1 2 1 2 2 1 2 1 2 0 2 0 1 2 2 1 1 1 2 2 0 2 2 0 1 2 1 0 0 0
#  0 2 2 0 2 1 0 2 0 0 2 0 1 1 2 2 0 0 0 2 0 2 2 1 0 2 1 2 0 2 0 2 2 0 1 2 0
#  0 0 2 2 2 1 2 1 0 1 0 2 1 2 1 2 0 2 2 0 0 1 0 1 2 1 0 0 1 2 0 2 1 2 2 1 2
#  1 1 2 2 1 2 1 1 2 2 2 2 0 2 2 0 2 0 1 1 1 2 0 2 0 1 2 2 0 2 2 0 2 2 0 1 0
#  2 1 0 2 2 2 0 0 1 1 1 0 1 0 1 2 2 0 2 0 2 2 2 1 1 2 2 2 0 0 2 2 0 0 2 2 2
#  2 1 2 1 1 1 0 2 2 1 2 2 2 1 2 2 2 0 0 2 0 2 0 0 0 1 2 2 0 2 1 2 2 2 2 1 2
#  1 2 1 2 2 2 2 2 2 0 2 1 1 2 2 2 2 0 1 1 0 2 0 1 2 2 0 2 2 2 2 2 2 2 2 1 2
#  1 1 2 1 2 2 0 2 2 0 1 2 2 2 2 0 0 1 1 0 2 2 1 2 1 1 2 1 2 0 0 2 0 1 2 2 1
#  0 0 1 2 2 2 0 2 1 2 2 2 0 2 1 1 2 2 2 0 0 2 2 2 1 2 2 0 2 0 1 1 1 2 2 1 2
#  2 1 2 2 1 0 2 1 2 1 0 2 2 1 1 2 2 1 0 2 0 0 0 2 0 2 1 2 2 0 1 2 0 1 0 0 1
#  2 2 2 2 0 1 0 2 2 1 2 2 2 2 1 0 1 2 2 2 1 1 2 0 1 2 2 0 2 1 1 2 2 0 2 2 2
#  2 2 2 2 0 1 2 1 1 2 1 0 2 0 2 1 1 2 1]
print(model.labels_)

# 成本
# 1388.1227163249318
print(model.inertia_)

# 实际迭代的次数
# 2
print(model.n_iter_)

# 成本的负数
# -1388.1227163249314
print(model.score(X))

Note:

score 计算的是成本的负数，越小表示成本越大，所以负数越大，成本越小，训练效果越好。一般 K-Means 使用轮廓系数来作为评价标准。 

轮廓系数

计算规则：

1. 针对样本空间中的一个特定样本，计算它与所在聚类其它样本的平均距离，表示为a
2. 再计算该样本与距离最近的另一个聚类中所有样本的平均距离，表示为b
3. 该样本的轮廓系数 =（b - a）/ max(a, b)
4. 聚类的轮廓系数 = 所有样本的轮廓系数的平均值
5. 取值范围为[-1, 1]，-1表示分类效果差，1表示分类效果好

from sklearn.metrics import silhouette_score

# 0.7088292431473303
print(silhouette_score(X, model.labels_))

plt.figure(figsize=(12, 8))
colors = ['r', 'b', 'y']

for n in range(3):
    cluster = X[model.labels_ == n]
    plt.scatter(cluster[:, 0], cluster[:, 1], s=50, marker='o', c=colors[n])

plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], marker='*', c='green', s=200)
plt.show()

结果数据分布图如下：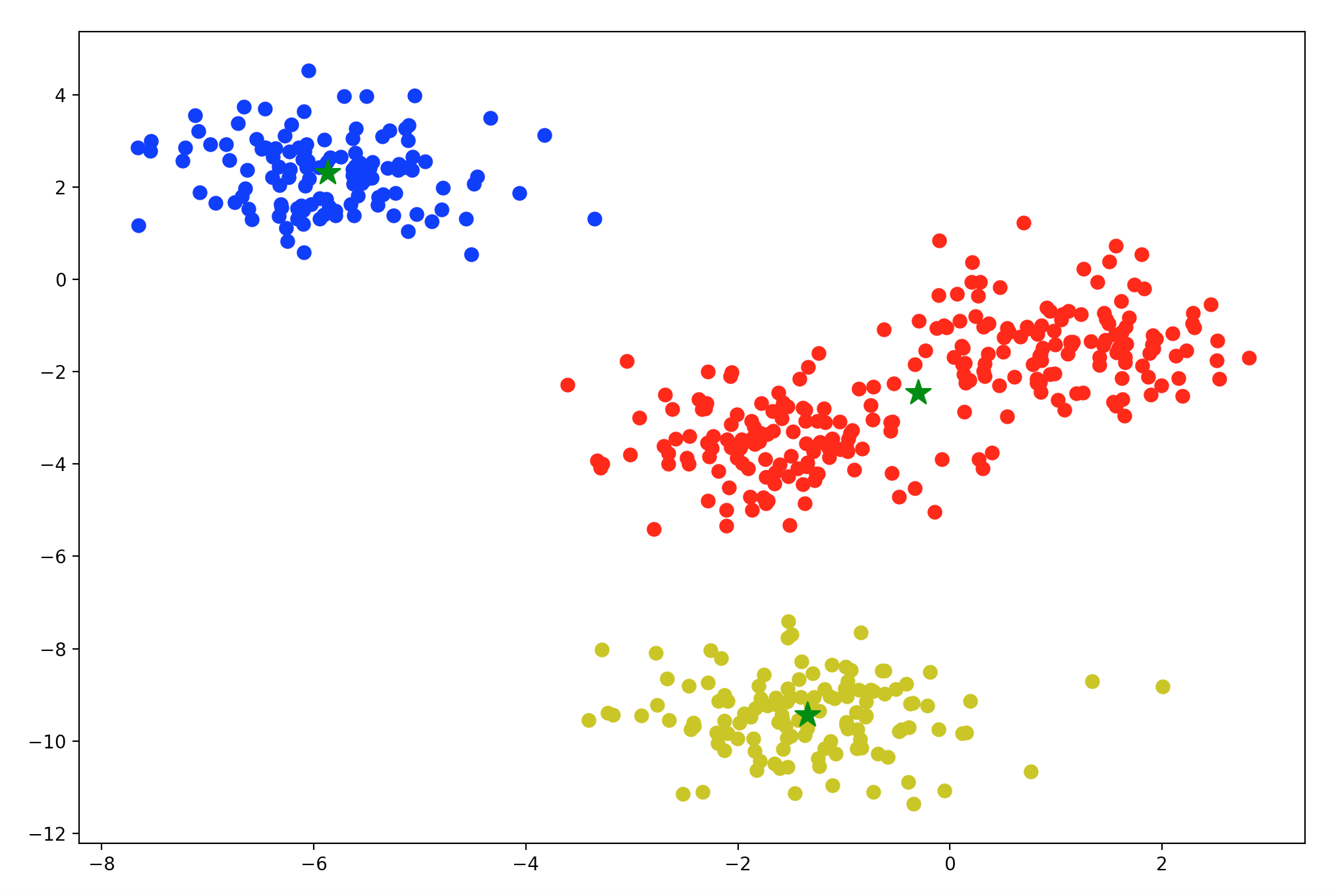

Summary

如何确定 K 类的中心点

其中包括了初始的设置，以及中间迭代过程中中心点的计算。在初始设置中，会进行 n_init 次的选择，然后选择初始中心点效果最好的为初始值。在每次分类更新后，都需要重新确认每一类的中心点，一般采用均值的方式进行确认。

如何将其他点划分到 K 类中

这里实际上是关于距离的定义，距离有多种定义的方式，在 K-Means 和 KNN 中，都可以采用欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离等。对于点的划分，就看它离哪个类的中心点的距离最近，就属于哪一类。

如何区分 K-Means 与 KNN

首先，这两个算法解决数据挖掘的两类问题。K-Means 是聚类算法，KNN 是分类算法。
这两个算法分别是两种不同的学习方式。K-Means 是无监督学习，也就是不需要事先给出分类标签，而 KNN 是有监督学习，需要给出训练数据的分类标识。
最后，K 值的含义不同。K-Means 中的 K 值代表 K 类。KNN 中的 K 值代表 K 个最接近的邻居。

监督学习和无监督学习区别

监督学习

• 目标明确
• 需要带标签的训练数据
• 效果容易评估

无监督学习

• 目标不明确
• 不需要带标签的数据
• 效果很难评估

Reference

https://time.geekbang.org/column/article/81390

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html

https://scikit-learn.org/stable/modules/generated/sklearn.metrics.silhouette_score.html