一.通用函数:快速的元素级数组函数
通用函数(ufunc)是一种对ndarray中的数据执行元素级运算的函数。我们可以将其看作简单函数(接受一个或多个标量,并产生一个或多个标量)的矢量化包装器。
许多通用函数都是简单的元素级变体,如sqrt和exp:
import numpy as np arr=np.arange(10) print(np.sqrt(arr)) ======================================== [0. 1. 1.41421356 1.73205081 2. 2.23606798 2.44948974 2.64575131 2.82842712 3. ] ======================================== print(np.exp(arr)) ======================================== [1.00000000e+00 2.71828183e+00 7.38905610e+00 2.00855369e+01 5.45981500e+01 1.48413159e+02 4.03428793e+02 1.09663316e+03 2.98095799e+03 8.10308393e+03] ========================================
下表列出了常用的一元ufunc和二元ufunc
一元ufunc
函数 |
说明 |
abs、fbs |
计算整数、浮点数或复数的绝对值。对于非复数值,可以使用更快的fbs |
sqrt |
计算各元素的平方根,相当于arr**0.5 |
square |
计算各元素的平方,相当于arr**2 |
exp |
计算各元素的指数e |
| log、log10、log2、log1p | 分别为自然对数(底数为e)、底数为10的log、底数为2的log、log(1+x) |
| sign | 计算各元素的正负号:1(正数)、0(零)、-1(负数) |
| ceil | 计算各元素的ceiling值,即大于等于该值的最小整数 |
| floor | 计算各元素的floor值,即小于等于该值的最大整数 |
| rint | 将各元素值四舍五入到最接近的整数,保留dtype |
| modf | 将数组的小数和整数部分以两个独立数组的形式返回 |
| isnan | 返回一个表示"哪些值是NaN(这不是一个数字)"的布尔型数组 |
| isfinite、isinf | 分别返回一个表示"哪些元素是有穷的(非inf,非NaN)"或"哪些元素是无穷的"的布尔型数组 |
| cos、cosh、sin、sinh、tan、tanh | 普通型和双曲型三角函数 |
| arccos、arccosh、arcsin、arcsinh、arctan、arctanh | 反三角函数 |
| logical_not | 计算各元素notx的真值。相当于-arr |
二元ufunc
| 函数 | 说明 |
| add | 将数组中对应的元素相加 |
| subtract | 从第一个数组中减去第二个数组中的元素 |
| multiply | 数组元素相乘 |
| divide、floor_divide | 除法或向下圆整除法(丢弃余数) |
| power | 对第一个数组中的元素A,根据第二个数组中的元素B,计算A的B次方 |
| maximum、fmax | 元素级的最大值计算。fmax将忽略NaN |
| minimum、fmin | 元素级的最小值计算。fmin将忽略NaN |
| mod | 元素级的求模计算(除法的余数) |
| copysign | 将第二个数组中的值的符号复制给第一个数组中的值 |
| greater、greater_equal、 less、less_equal、equal、not_equal |
执行元素级的比较运算,最终产生布尔型数组。相当于中缀运算符>、>=、<、<=、==、!= |
| logical_and、logical_or、logical_xor | 执行元素级的真值逻辑运算。相当于中缀运算符&、|、^ |
二.利用数组进行数据处理
Numpy数组使我们可以将许多种数据处理任务表述为简洁的数组表达式(否则需要编写循环)。用数组表达式代替循环的做法,通常被称为矢量化。一般来说矢量化数组运算要比等价的纯Python方式快上一两个数量级(甚至更多),尤其是各种数值计算。
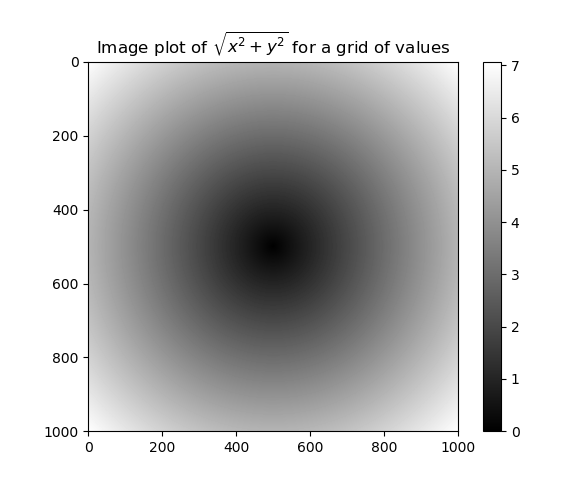
假设我们想在一组值(网格型)上计算函数sqrt(x^2+y^2),np.meshgrid函数接受两个一维数组,并产生两个二维矩阵(对应于两个数组中所有的(x,y)对)
#coding:utf-8 import matplotlib.pyplot as plt import numpy as np points=np.arange(-5,5,0.01) #1000个间隔相等的点 xs,ys=np.meshgrid(points,points) print(xs) print(ys) [[-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] ... [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99]] ======================================== [[-5. -5. -5. ... -5. -5. -5. ] [-4.99 -4.99 -4.99 ... -4.99 -4.99 -4.99] [-4.98 -4.98 -4.98 ... -4.98 -4.98 -4.98] ... [ 4.97 4.97 4.97 ... 4.97 4.97 4.97] [ 4.98 4.98 4.98 ... 4.98 4.98 4.98] [ 4.99 4.99 4.99 ... 4.99 4.99 4.99]]
现在把这两个数组当做两个浮点数那样编写表达式即可
z = np.sqrt(xs ** 2 + ys ** 2) print(z) ======================================== [[7.07106781 7.06400028 7.05693985 ... 7.04988652 7.05693985 7.06400028] [7.06400028 7.05692568 7.04985815 ... 7.04279774 7.04985815 7.05692568] [7.05693985 7.04985815 7.04278354 ... 7.03571603 7.04278354 7.04985815] ... [7.04988652 7.04279774 7.03571603 ... 7.0286414 7.03571603 7.04279774] [7.05693985 7.04985815 7.04278354 ... 7.03571603 7.04278354 7.04985815] [7.06400028 7.05692568 7.04985815 ... 7.04279774 7.04985815 7.05692568]]
plt.imshow(z, cmap=plt.cm.gray) plt.colorbar() plt.title("Image plot of $sqrt{x^2+y^2}$ for a grid of values") plt.show() #显示图形
1.将条件逻辑表述为数组运算
#numpy.where函数是三元表达式x if condition else y 的矢量化版本。假设我们有一个布尔数组和两个值数组
xarr=np.array([6.1,6.2,6.3,6.4,6.5])
yarr=np.array([8.1,8.2,8.3,8.4,8.5])
cond=np.array([True,False,True,False,True])
#现在我们想根据cond中的值选取xarr和yarr的值:当cond为True,选取xarr的值,否则选取yarr的值。列表推导式的做法如下:
result=[(x if z else y) for x,y,z in zip(xarr,yarr,cond)]
print(result)
#这样做有几个问题,第一:它对大数组的处理速度不是很快(因为所有工作都是纯python完成的),第二:无法用于多维数组。
#若用np.where,则可以将该功能写的非常简洁
result=np.where(cond,xarr,yarr)
print(result)
#np.where 的第二个和第三个参数不必是数组,它们都可以是标量值。在数据分析工作中,where通常用于根据另一个数组产生一个新的数组。
#假设有一个随机数组组成的矩阵,我们希望将所有正值替换为2,所有负值替换为-2,若利用np.where,则会非常简单
arr=np.random.randn(4,4)
print(arr)
new_arr=np.where(arr>0,2,-2)
# print(new_arr)
# print(np.where(arr>0,2,arr)) #只将正值设置为2
# print(np.where(arr<0,0,arr))#只将负值设置为0
#总结:
#np.where 有两种用法:
#第一种用法np.where(conditions,x,y) if (condituons成立):数组变x else:数组变y,例子如上
#第二种用法np.where(conditions)相当于给出数组的下标
#一维数组
x = np.arange(16)
print(x[np.where(x>5)])
#输出:(array([ 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], dtype=int64),)
#二维数组
x = np.arange(16).reshape(4,4)
print(x)
print(np.where(x>5)) #这里的坐标是前面的是一维的坐标,后面是二维的坐标
2.数学和统计方法
可以通过数组上的一组数学函数对整个数组或某个轴向的数据进行统计计算。
arr=np.random.randn(5,4)
print(arr)
print(arr.mean())#axis 不设置值,对 m*n 个数求均值,返回一个实数
print(arr.sum())
print(arr.mean(axis=1)) #axis =1 :对各行求均值,返回 m 个元素的一维数组
print(arr.mean(axis=0)) #axis = 0:对各列求均值,返回 n个元素的一维数组
#其他如cumsum、cumprod之类的方法则不聚合,而是产生一个由中间结果组成的数组
arr1=np.array([[1,2,3],[4,5,6]])
print(arr1.cumsum(0)) #每列对应元素累计相加
print(arr1.cumsum(1)) #每行对应元素累计相加
print(arr1.cumprod(0))#每列对应元素累计相乘
print(arr1.cumprod(1)) #每行对应元素累计相乘
基本数组统计方法
方法 |
说明 |
sum |
对数组中全部或某轴向的元素求和。零长度的数组的sum为0 |
mean |
算术平均值。零长度的数组的mean为NaN |
std、var |
分别为标准差和方差,自由度可调(默认为n) |
max、min |
最大值和最小值 |
argmin、argmax |
分别为最小和最大元素的索引 |
cumsum |
所有元素的累计和 |
cumprod |
所有元素的累计积 |
#排序
#跟Python内置的列表类型一样,Numpy数组也可以通过sort方法排序
arr=np.array([[1,4,2],[7,2,6]])
print(arr.sort(0)) #对0轴排序,每列从小到大排序
print(arr)
print(arr.sort(1)) #对1轴排序,每行从小到大排序
print(arr)
#唯一化以及其他的集合逻辑
#Numpy提供了一些针对一维ndarray的基本集合运算。最常用的可能要数np.unique了,它用于找出数组中的唯一值并返回已排序的结果
names=np.array(['Kobe','Calvin','Michale','James','Calvin','Kobe','Kobe','Calvin'])
print(np.unique(names))
numbers=np.array([2,3,8,5,8,8,24,1,6,3])
print(np.unique(numbers))
Numpy中的集合函数如下表:
方法 |
说明 |
unique(x) |
计算x中的唯一元素,并返回有序结果 |
intersect1d(x,y) |
计算x和y中的公共元素,并返回有序结果 |
union1d(x,y) |
计算x和y的并集,并返回有序结果 |
in1d(x,y) |
得到一个表示"x的元素是否包含于y"的布尔型数组 |
setdiff1d(x,y) |
集合额差,即元素在x中且不在y中 |
cumprod |
所有元素的累计积 |