P1736 创意吃鱼法

题目描述

回到家中的猫猫把三桶鱼全部转移到了她那长方形大池子中，然后开始思考：到底要以何种方法吃鱼呢（猫猫就是这么可爱，吃鱼也要想好吃法 ^_*）。她发现，把大池子视为01矩阵（0表示对应位置无鱼，1表示对应位置有鱼）有助于决定吃鱼策略。

在代表池子的01矩阵中，有很多的正方形子矩阵，如果某个正方形子矩阵的某条对角线上都有鱼，且此正方形子矩阵的其他地方无鱼，猫猫就可以从这个正方形子矩阵“对角线的一端”下口，只一吸，就能把对角线上的那一队鲜鱼吸入口中。

猫猫是个贪婪的家伙，所以她想一口吃掉尽量多的鱼。请你帮猫猫计算一下，她一口下去，最多可以吃掉多少条鱼？

输入输出格式

输入格式：

有多组输入数据，每组数据：

第一行有两个整数n和m（n,m≥1），描述池塘规模。接下来的n行，每行有m个数字（非“0”即“1”）。每两个数字之间用空格隔开。

对于30%的数据，有n,m≤100

对于60%的数据，有n,m≤1000

对于100%的数据，有n,m≤2500

输出格式：

只有一个整数——猫猫一口下去可以吃掉的鱼的数量，占一行，行末有回车。

输入输出样例

输入样例#1： 复制

4 6
0 1 0 1 0 0
0 0 1 0 1 0
1 1 0 0 0 1
0 1 1 0 1 0

输出样例#1： 复制

3

说明

右上角的

1 0 0
0 1 0
0 0 1

---

(O(n*m))
单调队列分两种方向线沿对角线进行枚举右下角或左下角，如果新枚举出的点是1但是这个点加上前一个的点作为右下角或左下角的合法正方形不合法，则将左端点不断后移直到合法为止。

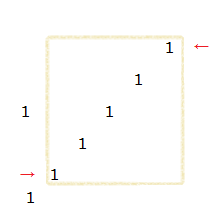
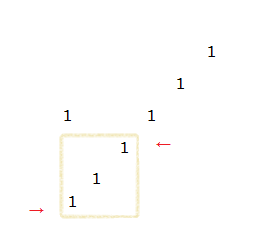
记录答案即可
（然鹅一看就很难写(小声

(O(n*m*log(n)))
递推记录每一个点最多延斜线向左上延伸长度和向右上延伸长度以及二维前缀和，每次二分出一个答案(k)时穷举每个点，如果这个点作为左上角，右下角可以向左上延伸长度(≥k)或左下角向右上延伸长度(≥k)且正方形的和(=k)则返回(true)

#include<iostream>
#include<cstdio>

using namespace std;

int i,m,n,j,k,a[2501][2501],x,y,b[2501][2501],l[2501][2501],r[2501][2501];
char c;

bool dfs(int now)
{
	for(int i=1;i<=n-now+1;i++)
		for(int j=1;j<=m-now+1;j++)
			if(((l[i+now-1][j+now-1]>=now)||(r[i+now-1][j]>=now))&&(b[i+now-1][j+now-1]-b[i-1][j+now-1]-b[i+now-1][j-1]+b[i-1][j-1]==now)) return 1; 
	return 0;
}

int ef(int l,int r)
{
	while(l<r)
	{
		int mid=(l+r+1)/2;
		if(dfs(mid)) l=mid;
		else r=mid-1;
	}
	return l;
}

int main()
{
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
		{
			scanf("%d",&a[i][j]);
			b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j];
		}
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			if(a[i][j]) l[i][j]=1+l[i-1][j-1];
	for(i=1;i<=n;i++)
		for(j=m;j>=1;j--)
			if(a[i][j]) r[i][j]=1+r[i-1][j+1];
	printf("%d",ef(0,min(n,m)));
}