UOJ #357. 【JOI2017春季合宿】Sparklers

Description

小S和小M去看花火大会。
一共有 n 个人按顺序排成一排，每个人手上有一个仅能被点燃一次的烟花。最开始时第 K 个人手上的烟花是点燃的。
烟花最多能燃烧 T 时间。每当两个人的位置重叠且其中一个人手上的烟花是点燃的时，另一个人手上的烟花可以被点燃。
现在小M想要知道，每个人至少需要以多快的速度 s 奔跑，才能使得每个人手中的烟花都能被点燃。
可怜的小M当然不会啦，所以她向你求助。

Solution

首先二分答案,算出一个人点燃烟花后最多可以走的距离 (s)
要猜一个结论:([i,j]) 个人传递完之后 , 这个时刻一个刚刚被点燃烟花的人 (j) 可以在的位置是一个区间
设 (L_{i,j}) 表示第 ([i,j]) 个人传递完之后 , 这个时刻一个刚刚被点燃烟花的人 (i) 可以在的位置的最小值
(R_{i,j}) 表示第 ([i,j]) 个人传递完之后 , 这个时刻一个刚刚被点燃烟花的人 (j) 可以在的位置的最大值
枚举 (k=i-1,j+1) 来转移
得到新的区间: ([L_{i,j}-s,R_{i,j}+s]∩[x_k-(i-j+1)*s,x_k+(i-j+1)*s])
要使这个区间不为空,那么:

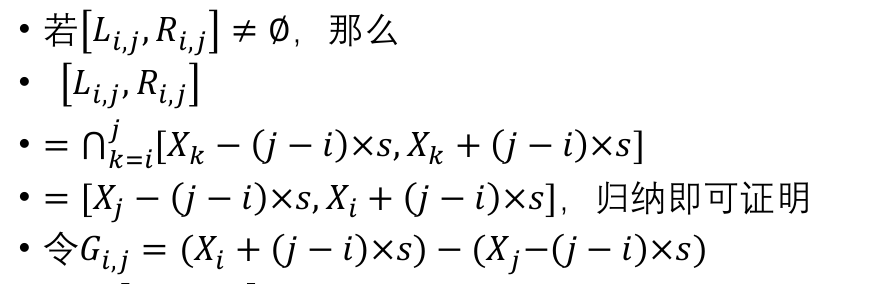
贪心的把左右端点往两边移动:
如果左端点可以在不小于右端点权值的情况下移动到更大的值,则移动过去,右端点同理
一个点被经过的次数似乎是 (2) 次

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
template<class T>void gi(T &x){
	int f;char c;
	for(f=1,c=getchar();c<'0'||c>'9';c=getchar())if(c=='-')f=-1;
	for(x=0;c<='9'&&c>='0';c=getchar())x=x*10+(c&15);x*=f;
}
typedef long long ll;
int n,T,K,x[N];ll a[N];
inline bool check(int s){
	for(int i=1;i<=n;i++)a[i]=x[i]-2ll*i*s;
	if(a[1]<a[n])return 0;
	int l,r,L=K,R=K,tl=K,tr=K;
	for(int i=K;i>=1;i--)if(a[i]>=a[L])L=i;
	for(int i=K;i<=n;i++)if(a[i]<=a[R])R=i;
	for(l=r=K;;){
		for(;tl>L&&a[tl-1]>=a[r];)if(a[--tl]>=a[l])break;
		for(;tr<R&&a[tr+1]<=a[l];)if(a[++tr]<=a[r])break;
		if(a[tl]<a[l])tl=l;if(a[tr]>a[r])tr=r;
		if(l==tl && r==tr)break;
		l=tl;r=tr;
	}
	if(l!=L||r!=R)return 0;
	for(tl=l=1,tr=r=n;;){
		for(;tl<L&&a[tl+1]>=a[r];)if(a[++tl]>=a[l])break;
		for(;tr>R&&a[tr-1]<=a[l];)if(a[--tr]<=a[r])break;
		if(a[tl]<a[l])tl=l;if(a[tr]>a[r])tr=r;
		if(l==tl  && r==tr)break;
		l=tl;r=tr;
	}
	return l==L&&r==R;
}
int main(){
  freopen("fireworks.in","r",stdin);
  freopen("fireworks.out","w",stdout);
  cin>>n>>K>>T;
  for(int i=1;i<=n;i++)gi(x[i]);
  int l=0,r=x[n]-x[1],mid,ret=0;
  while(l<=r){
	  mid=(l+r)>>1;
	  if(check(mid))ret=mid,r=mid-1;
	  else l=mid+1;
  }
  cout<<(ret+T-1)/T;
  return 0;
}