二维爬山扫描算法求最大值

#测试算法
import numpy as  np
pointdata=np.random.randint(1,100,size=(1000,2))
print(pointdata)
score=np.random.randn(1000)
score=score.reshape(-1,1)
print(score)
finaldata=np.hstack((pointdata,score))
print(finaldata)

#实时输出坐标轴x,y
def output(x,y):
    return -x**2-y**2-x*y+4*x
'''
def output(x,y):
    score=finaldata(x,y)
    return score
'''

def test(x0,y0,fanx,fany):
    #定义初始值的大小
    point_x=x0
    point_y=y0

    step=0.001
    point_history=[]
    score_history=[]

    i=0
    while (point_x<fanx[1] and point_x>fanx[0]) and (point_y<fany[1] and point_y>fany[0]) and i<1e4:
        x0=point_x
        y0=point_y
        while point_x<fanx[1] and point_x>fanx[0]:

            last_point_x=point_x
            gradient = (output(point_x+step, point_y) - output(point_x, point_y)) / step
            point_x=point_x+step*np.sign(gradient)

            if abs(output(point_x,point_y)-output(last_point_x,point_y))<0.0001:
                print(point_x)
                point_history.append((point_x,point_y))
                score_history.append(output(point_x,point_y))
                break

        while point_y<fany[1] and point_y>fany[0]:

            last_point_y = point_y
            gradient = (output(point_x, point_y+step) - output(point_x, point_y)) / step
            point_y = point_y + step * np.sign(gradient)

            if abs(output(point_x,point_y)-output(point_x,last_point_y))<0.00001:
                point_history.append((point_x, point_y))
                score_history.append(output(point_x, point_y))
                print(point_y)
                break

        if abs(output(point_x, point_y) - output(x0, y0)) < 0.0000001 or abs(point_x-x0) < 0.00001:
            break
        i=i+1
    print(point_x, point_y,x0, y0)

test(2,8,[-10,10],[-10,10])

# 画出图像如下进行检查
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib import pyplot as plt

fig = plt.figure(figsize=(10,6))
ax = Axes3D(fig)
x = np.arange(-10, 10, 0.5)
y = np.arange(-10, 10, 0.5)
X, Y = np.meshgrid(x, y)
Z =-X**2 - Y**2-X*Y+4*X
plt.xlabel('x')
plt.ylabel('y')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
print(Z)
print(np.max(Z))

二维爬山扫描算法

1. 算法思想：

爬山扫描算法主体思想是采用分轴迭代的思路，对每个轴依次进行最优值的寻找，然后不断进行循环迭代，最后找到整体最大值时的参数组合。其中，分轴迭代算法主要思想是在限制另外一个轴数据一定的情况下使用单轴梯度上升法求得单轴最大值时的变量取值。

另外，由于使用场景是实时传出的测量数据，所以数据之间不存在具体的二维函数表达式，只是由数据不断测量累计的数据集合。在这种情况下，使用梯度上升方法求最值时，不能用求导的形式来求得，只可使用梯度代替方法，即：

 

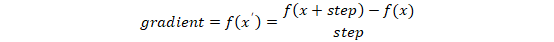
另外，由于数据不是离线进行积累的，所以在使用梯度上升法时不能直接在原来的数据初始点上加以梯度*步长，因为在数据初始点开始时一般梯度值很大，所以单轴数据更替变化太大，新的数据点下的指标实时测量不到，所以为了保证在实时中数据的可测量性，我们最好使用固定的步长（并且数据更新需要慢于实时测量的速度）来进行单轴数据的更替，即单轴数据更替表达式为：

 

其中sign(x)是取数字的正负号函数：

 

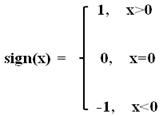
       使用sign(x)*gradient更替的好处就是单轴自变量依旧可以按照梯上升的方向进行最大值的寻找，并且可以控制步长大小来和实时测量传输数据的速度进行匹配。

1. 算法步骤：

整体算法主要可以分为以下几步：

（1）    在约束范围里初始化开始点point（）；

（2）    判断初始点是否在规定的参数范围中，如果在，则往下进行第三步；不在则结束算法；

（3）    固定y轴不变，进行x轴的移动，基于实时测量的数据进行梯度上升的最大值寻找，直到达到x轴的指标最高点（或者接近最高点的位置），记录此时的，其核心在于：

y轴固定不变，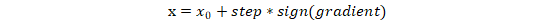

（4）    固定x轴不变，即x=，之后基于y轴利用梯度上升法进行y轴指标最大值的寻找，并将达到最大值时的y记为，此时核心是：

x轴固定不变，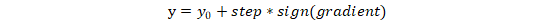

（5）    循环（2）（3）步骤，直到每一次x,y轴迭代前后指标值相差小于一定的阈值时，可以认为已经达到最大值（此外，为了防止迭代次数太多，可以设置一定的迭代次数限制参数）；

（6）    结束算法，输此时的x和y的值。

整体的算法流程如下图所示：

  

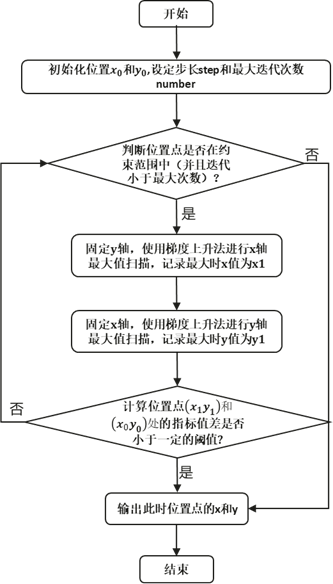
图 二维扫描爬山算法流程图

1. 算法测试：

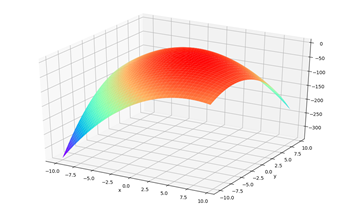
（1）对于基础测量的数据集形成的如下二维图像：

  

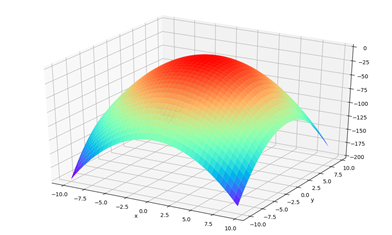
图 二维数据点集图像

x和y的约束范围为-10到10，此时利用算法求得最优解为：x=y=0，最优解为0，是正确的；

（2）换一种数据集形成的图像形式：

1.  

x和y的约束范围为-10到10，此时利用算法求得最优解为：x=2.67，y=-1.33，最优解为5.3，是正确的；

1. 源代码：

#实时输出测量值函数（x,y为位置坐标，返回的score为此位置处的指标测量值大小）

'''

def output(x,y):

    score=finaldata(x,y)

    return score

'''

#整体的扫描算法函数

def test(x0,y0,fanx,fany):

    #定义初始位置x0,y0

    point_x=x0

    point_y=y0

    #定义爹迭代扫描的步长大小step

    step=0.001

    point_history=[]

    score_history=[]

   #定义目前的迭代次数

    i=0

#定义最大的迭代次数

number=1e4

           #判断继续进行迭代的条件：在约束范围里并且迭代次数小于规定次数

    while (point_x<fanx[1] and point_x>fanx[0]) and (point_y<fany[1] and point_y>fany[0]) and i<number:

        x0=point_x

        y0=point_y

        #固定y轴，x轴单轴的最大值扫描

        while point_x<fanx[1] and point_x>fanx[0]:

            last_point_x=point_x

            gradient = (output(point_x+step, point_y) - output(point_x, point_y)) / step

            point_x=point_x+step*np.sign(gradient)

            if abs(output(point_x,point_y)-output(last_point_x,point_y))<0.0001:

                print(point_x)

                point_history.append((point_x,point_y))

                score_history.append(output(point_x,point_y))

                break

        #固定x轴，y轴单轴的最大值扫描

        while point_y<fany[1] and point_y>fany[0]:

            last_point_y = point_y

            gradient = (output(point_x, point_y+step) - output(point_x, point_y)) / step

            point_y = point_y + step * np.sign(gradient)

            if abs(output(point_x,point_y)-output(point_x,last_point_y))<0.00001:

                point_history.append((point_x, point_y))

                score_history.append(output(point_x, point_y))

                print(point_y)

                break

              #判断一次x,y轴迭代之后指标值的差距是否足够小，达到阈值之后默认已经到最高点或者接近最高点

        if abs(output(point_x, point_y) - output(x0, y0)) < 0.0000001 or abs(point_x-x0) < 0.00001:

            break

        i=i+1

    print(point_x, point_y)  #输出最终最高点的位置坐标x和y