[ZJOI2017]树状数组

Description

漆黑的晚上，九条可怜躺在床上辗转反侧。难以入眠的她想起了若干年前她的一次悲惨的OI 比赛经历。那是一道

基础的树状数组题。给出一个长度为 n 的数组 A，初始值都为 0，接下来进行 m 次操作，操作有两种：

1 x，表示将 Ax 变成 (Ax + 1) mod 2。

2 l r，表示询问 sigma(Ai) mod 2,L<=i<=r

尽管那个时候的可怜非常的 simple，但是她还是发现这题可以用树状数组做。当时非常young 的她写了如下的算

法：

其中 lowbit(x) 表示数字 x 最?的非 0 二进制位，例如 lowbit(5) = 1, lowbit(12) = 4。进行第一类操作的时

候就调用 Add(x)，第二类操作的时候答案就是 Query(l, r)。如果你对树状数组比较熟悉，不难发现可怜把树状

数组写错了： Add和Find 中 x 变化的方向反了。因此这个程序在最终测试时华丽的爆 0 了。然而奇怪的是，在

当时，这个程序通过了出题人给出的大样例——这也是可怜没有进行对拍的原因。现在，可怜想要算一下，这个程

序回答对每一个询问的概率是多少，这样她就可以再次的感受到自己是一个多么非的人了。然而时间已经过去了很

多年，即使是可怜也没有办法完全回忆起当时的大样例。幸运的是，她回忆起了大部分内容，唯一遗忘的是每一次

第一类操作的 x的值，因此她假定这次操作的 x 是在 [li, ri] 范围内等概率随机的。具体来说，可怜给出了

一个长度为 n 的数组 A，初始为 0，接下来进行了 m 次操作：

1 l r，表示在区间 [l, r] 中等概率选取一个 x 并执行 Add(x)。

2 l r，表示询问执行 Query(l, r) 得到的结果是正确的概率是多少。

Input

第一行输入两个整数 n, m。

接下来 m 行每行描述一个操作，格式如题目中所示。

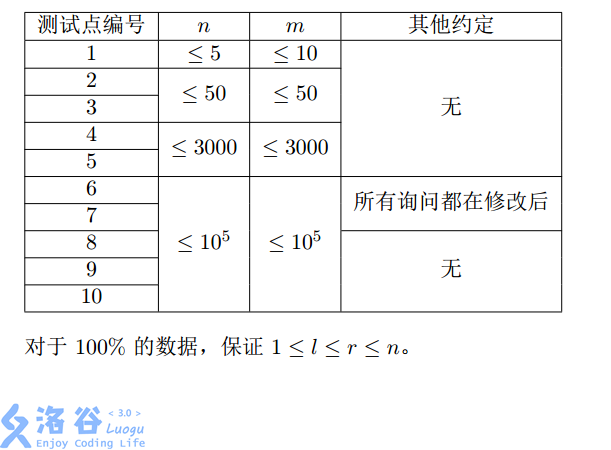
N<=10^5,m<=10^5,1<=L<=R<=N

Output

对于每组询问，输出一个整数表示答案。如果答案化为最简分数后形如 x/y

，那么你只需要输出 x*y^-1 mod 998244353 后的值。（即输出答案模 998244353）。

Sample Input

5 5
1 3 3
2 3 5
2 4 5
1 1 3
2 2 5

Sample Output

1
0
665496236
//在进行完 Add(3) 之后， A 数组变成了 [0, 1, 1, 0, 0]。所以前两次询问可怜的程序答案都是
1，因此第一次询问可怜一定正确，第二次询问可怜一定错误。

数据范围

查询(l,r)从前缀变为了后缀

那么原来是S[r]-s[l-1]，变成了S[l-1]-s[r]

原来的区间是[l,r]，现在变成了[l-1,r-1]

询问要正确就要求l-1和r的值必须一样

当l=1时

S[r]-s[0]=>s[0]-s[r]=-s[r]

所以此时要正确就必须使1～r的前缀和与r～n的前缀和相同

将查询(l-1,r)用一个点表示

修改[l,r]的一个数，分成几种情况讨论：

1.使询问的值一样的概率：

(1):x属于[1,l-1]，y属于[l,r].此时要相同必须要求y不被选中，概率(1-p)

(2):y属于[r+1,n],x属于[l,r].此时同上，x不能被选中

(3):x,y同属于[l,r].x,y都不能被选中，概率(1-2p)

2.使询问的r的前缀和等于后缀和的概率：x为0

(1):y属于[0,l-1].因为[l,r]总会改一个数，所以概率为0

(2):y属于[r+1,n+1].同上

(3):y属于[l,r].要求选中y，概率为p

修改用树套树(二维线段树)，外层的树维护第一维坐标，内层的树维护第二维坐标

不过空间不够，要动态开点

如何合并两次修改:假设两次的相同概率分别为p1,p2(以上2种情况统称相同)

显然新的概率为:p1*p2+(1-p1)*(1-p2)

都不相同合起来就相同了

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cmath>
 6 using namespace std;
 7 typedef long long lol;
 8 lol Mod=998244353;
 9 int size,root[400001],ch[30000001][2],n,m;
10 int ans,sum[30000001];
11 int merge(lol x,lol y)
12 {
13   return (x*y%Mod+(1-x+Mod)*(1-y+Mod)%Mod)%Mod;
14 }
15 lol qpow(lol x,int y)
16 {
17   lol res=1;
18   while (y)
19     {
20       if (y&1) res=res*x%Mod;
21       x=x*x%Mod;
22       y>>=1;
23     }
24   return res;
25 }
26 void update2(int &rt,int l,int r,int L,int R,lol v)
27 {
28   if (!rt) rt=++size,sum[rt]=1;
29   if (l>=L&&r<=R)
30     {
31       sum[rt]=merge(sum[rt],v);
32       return;
33     }
34   int mid=(l+r)>>1;
35   if (L<=mid) update2(ch[rt][0],l,mid,L,R,v);
36   if (R>mid) update2(ch[rt][1],mid+1,r,L,R,v);
37 }
38 void update1(int rt,int l,int r,int L,int R,int LL,int RR,lol v)
39 {
40   if (l>=L&&r<=R)
41     {
42       update2(root[rt],0,n+1,LL,RR,v);
43       return;
44     }
45   int mid=(l+r)>>1;
46   if (L<=mid) update1(rt<<1,l,mid,L,R,LL,RR,v);
47   if (R>mid) update1(rt<<1|1,mid+1,r,L,R,LL,RR,v);
48 }
49 void query2(int rt,int l,int r,int x1)
50 {
51   if (!rt) return;
52   ans=merge(ans,sum[rt]);
53   if (l==r) return;
54   int mid=(l+r)>>1;
55   if (x1<=mid) query2(ch[rt][0],l,mid,x1);
56   else query2(ch[rt][1],mid+1,r,x1);
57 }
58 void query1(int rt,int l,int r,int x1,int x2)
59 {
60   if (root[rt]) query2(root[rt],0,n+1,x2);
61   if (l==r)
62       return;
63   int mid=(l+r)>>1;
64   if (x1<=mid) query1(rt<<1,l,mid,x1,x2);
65   else query1(rt<<1|1,mid+1,r,x1,x2);
66 }
67 int main()
68 {int i,opt,l,r;
69   cin>>n>>m;
70   for (i=1;i<=m;i++)
71     {
72       scanf("%d%d%d",&opt,&l,&r);
73       if (opt==1)
74     {
75       lol p=qpow(r-l+1,Mod-2);
76       if (l>1) update1(1,0,n,1,l-1,l,r,(1-p+Mod)%Mod);
77       if (r<n) update1(1,0,n,l,r,r+1,n,(1-p+Mod)%Mod);
78       lol pp=p*2%Mod;
79       update1(1,0,n,l,r,l,r,(1-pp+Mod)%Mod);
80       update1(1,0,n,0,0,0,l-1,0);
81       update1(1,0,n,0,0,r+1,n+1,0);
82       update1(1,0,n,0,0,l,r,p);
83     }
84       else
85     {
86       ans=1;
87       query1(1,0,n,l-1,r);
88       printf("%d
",ans);
89     }
90     }
91 }