Description
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,
而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
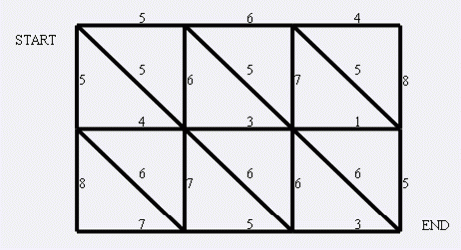
左上角点为((1,1)), 右下角点为((N,M))(上图中(N=3),(M=4)).有以下三种类型的道路:
- ((x,y) ightleftharpoons(x+1,y))
- ((x,y) ightleftharpoons(x,y+1))
- ((x,y) ightleftharpoons(x+1,y+1))
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的。左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角((1,1))的窝里,现在它们要跑到右下角((N,M))的窝中去,狼王开始伏击这些兔子。当然为了保险起见,如果一条道路上最多通过的兔子数为(K),狼王需要安排同样数量的(K)只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
Input
第一行两个整数(N,M),表示网格的大小。
接下来分三部分。
第一部分共 (N) 行,每行 (M-1) 个数,表示横向道路的权值。
第二部分共 (N-1) 行,每行 (M) 个数,表示纵向道路的权值。
第三部分共 (N-1) 行,每行 (M-1) 个数,表示斜向道路的权值。
Output
输出一个整数,表示参与伏击的狼的最小数量。
Sample Input
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
Sample Output
14
HNIT
对于全部的测试点,保证(3 leqslant N,M leqslant 1000),所有道路的权值均为不超过(10^6)的正整数。
这题一看就是个最小割板子题,不过当你笑嘻嘻敲一个Dinic上去后肯定会得到TLE的结果(卡常大佬不在此列)
那就换个方法,这题求最小割肯定是没错的,关键是怎么快速的求。
可以发现,这个图的边是没有交叉的,因此它是一张平面图,因此,我们可以使用一个性质:平面图最小割=对偶图最短路
证明过程可以画图理解,对偶图定义请自行查询,这里不再赘述
找对建图方法即可
/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
static char buf[1000000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
int f=1; char ch=gc();
for (;ch<'0'||ch>'9';ch=gc()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
template<typename T>inline T read(T x){
int f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+'0');
}
template<typename T>inline T min(T x,T y){return x<y?x:y;}
template<typename T>inline T max(T x,T y){return x>y?x:y;}
template<typename T>inline T swap(T &x,T &y){T t=x; x=y,y=t;}
const int N=2e6;
struct S1{
#define ls (p<<1)
#define rs (p<<1|1)
#define fa (p>>1)
struct S2{
int x,v;
S2(){x=v=0;}
S2(int _x,int _v){x=_x,v=_v;}
void insert(int _x,int _v){x=_x,v=_v;}
bool operator <(const S2 &_x){return v<_x.v;}
}Q[N+10];
int tot;
S1(){tot=0;}
void clear(){tot=0;}
void insert(int x,int v){
Q[++tot].insert(x,v);
int p=tot;
while (Q[p]<Q[fa]) swap(Q[p],Q[fa]),p=fa;
}
S2 Query(){
S2 Ans=Q[1]; Q[1]=Q[tot--];
int p=1,son;
while (ls<=tot){
if (rs>tot||Q[ls]<Q[rs]) son=ls;
else son=rs;
if (Q[son]<Q[p]) swap(Q[p],Q[son]),p=son;
else break;
}
return Ans;
}
bool empty(){return !tot;}
#undef ls
#undef rs
#undef fa
}Heap;
bool vis[N+10];
int now[N+10],pre[(N<<3)+10],child[(N<<3)+10],val[(N<<3)+10],dis[N+10],tot;
void join(int x,int y,int v){pre[++tot]=now[x],now[x]=tot,child[tot]=y,val[tot]=v;}
void insert(int x,int y,int v){join(x,y,v),join(y,x,v);}
void Dijkstra(int S){
memset(dis,63,sizeof(dis));
Heap.insert(S,dis[S]=0);
while (!Heap.empty()){
int Now=Heap.Query().x;
if (vis[Now]) continue;
vis[Now]=1;
for (int p=now[Now],son=child[p];p;p=pre[p],son=child[p]){
if (dis[son]>dis[Now]+val[p]){
dis[son]=dis[Now]+val[p];
Heap.insert(son,dis[son]);
}
}
}
}
int main(){
int n=read(0),m=read(0),S=(n-1)*(m-1)*2+1,T=S+1;
for (int i=1;i<=n;i++){
for (int j=1;j<m;j++){
int V=read(0);
if (i==1) insert(S,j,V);
if (i==n) insert(S+j-m,T,V);
if (i!=1&&i!=n) insert((i-1)*(m-1)+j,(n+i-3)*(m-1)+j,V);
}
}
for (int i=1;i<n;i++){
for (int j=1;j<=m;j++){
int V=read(0);
if (j==1) insert((n+i-2)*(m-1)+1,T,V);
if (j==m) insert(i*(m-1),S,V);
if (j!=1&&j!=m) insert((i-1)*(m-1)+j-1,(n+i-2)*(m-1)+j,V);
}
}
for (int i=1;i<n;i++){
for (int j=1;j<m;j++){
int V=read(0);
insert((i-1)*(m-1)+j,(n+i-2)*(m-1)+j,V);
}
}
Dijkstra(S);
printf("%d
",dis[T]);
return 0;
}