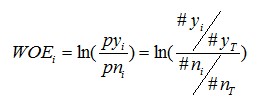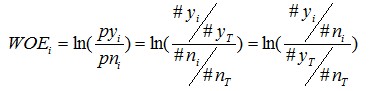woe全称是“Weight of Evidence”,即证据权重,是对原始自变量的一种编码形式。
进行WOE编码前,需要先把这个变量进行分组处理(离散化)
其中,pyi是这个组中响应客户(即模型中预测变量取值为“是”或1的个体,也叫坏样本)占所有样本中所有响应客户的比例,pni是这个组中未响应客户(也叫好样本)占样本中所有未响应客户的比例;
#yi是这个组中响应客户的数量,#ni是这个组中未响应客户的数量,#yT是样本中所有响应客户的数量,#nT是样本中所有未响应客户的数量。
从这个公式中我们可以体会到,WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。
为了更简单明了一点,我们来做个简单变换,得:
不难看出,woe表示的是当前这个组中响应客户和未响应客户的比值,和所有样本中这个比值的差异。这个差异是用这两个比值的比值,再取对数来表示的。例子如下:
| Age | #bad | #good | Woe |
|---|---|---|---|
| 0-10 | 50 | 200 | =ln((50/100)/(200/1000))=ln((50/200)/(100/1000)) |
| 10-18 | 20 | 200 | =ln((20/100)/(200/1000))=ln((20/200)/(100/1000)) |
| 18-35 | 5 | 200 | =ln((5/100)/(200/1000))=ln((5/200)/(100/1000)) |
| 35-50 | 15 | 200 | =ln((15/100)/(200/1000))=ln((15/200)/(100/1000)) |
| 50以上 | 10 | 200 | =ln((10/100)/(200/1000))=ln((10/200)/(100/1000)) |
| 汇总 | 100 | 1000 |
WOE越大,这种差异越大,这个分组里的样本响应的可能性就越大,WOE越小,差异越小,这个分组里的样本响应的可能性就越小。woe反映的是在自变量每个分组下违约用户对正常用户占比和总体中违约用户对正常用户占比之间的差异;从而可以直观的认为woe蕴含了自变量取值对于目标变量(违约概率)的影响。再加上woe计算形式与logistic回归中目标变量的logistic转换(logist_p=ln(p/1-p))如此相似,因而可以将自变量woe值替代原先的自变量值。
那woe编码有什么意义呢?
很明显,它可以提升模型的预测效果,提高模型的可理解性。
-
标准化的功能。
WOE编码之后,自变量其实具备了某种标准化的性质,也就是说,自变量内部的各个取值之间都可以直接进行比较(WOE之间的比较)
-
异常值处理。
一些极值变量,可以通过分组的WOE,变为非异常值
- 检查变量WOE后与违约概率的关系
一般筛选的变量WOE与违约概率都是单调的,如果出现U型,或者其他曲线形状,则需要重新看下变量是否有问题。
-
核查WOE变量模型的变量系数出现负值。
如果最终模型的出来的系数出现负值,需要考虑是否出现了多重共线性的影响,或者变量计算逻辑问题。
woe的意义,大家可以再体会一下。下面附上一段woe自编Code:
## 证据权重函数
def total_response(data,label):
value_count = data[label].value_counts()
return value_count
def woe(data,feature,label,label_value):
'''
data:传入需要做woe的特征和标签两列数据
feature:特征名
label:标签名
label_value:接收字典,key为1,0,表示为响应和未响应,value为对应的值
'''
import pandas as pd
import numpy as np
idx = pd.IndexSlice # 创建一个对象以更轻松地执行多索引切片
data['woe'] = 1
groups = data.groupby([label,feature]).count().sort_index()
## 使用上述函数
value_counts = total_response(data,label)
resp_col = label_value[1]
not_resp_col = label_value[0]
resp = groups.loc[idx[resp_col,:]]/value_counts[resp_col]
not_resp = groups.loc[idx[not_resp_col,:]]/value_counts[not_resp_col]
Woe = np.log(resp/not_resp).fillna(0)
return Woe
既然讲到这了,就再讲讲IV吧。
公式如下:

有了一个变量各分组的IV值,我们就可以计算整个变量的IV值,方法很简单,就是把各分组的IV相加:

其中,n为变量分组个数。