定义
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。
该序列必须满足下面两个条件:
① 每个顶点出现且只出现一次。
② 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
实现
AOV网
定义
AOV网(Activity On Vertex NetWork)用顶点表示活动,边表示活动(顶点)发生的先后关系。
AOV网的边不设权值,若存在边<a,b>则表示活动a必须发生在活动b之前。
解决
① 在网中选择一个入度为0的顶点输出
② 在图中删除该顶点及所有以该顶点为头的边
重复上述过程,直至所有边均被输出。
若图中还有点未输出,则图中必有环。
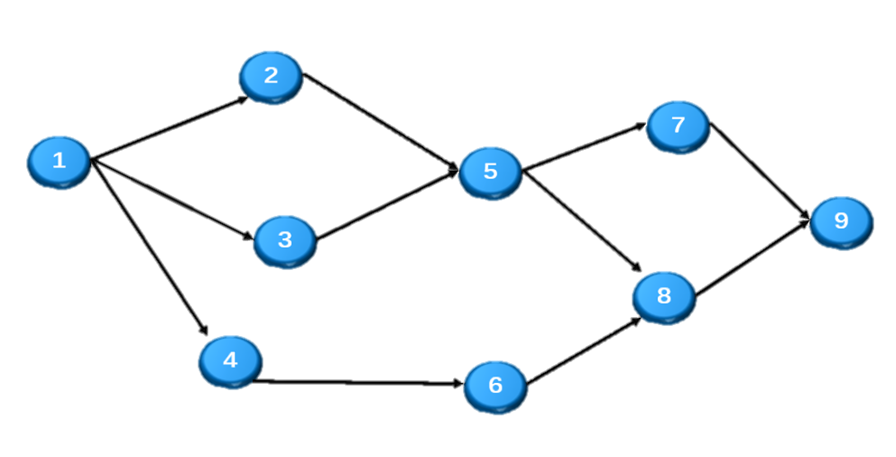
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=10005;
struct node
{
int v,next;
node(){}
node(int a,int b)
{v=a;next=b;}
}e[maxn];
int head[maxn],indegree[maxn],n,m;
int topo();
int main()
{
fill(head,head+maxn,-1);
int u,v,w,cnt=1;
scanf("%d%d",&n,&m);
while(m--)
{
scanf("%d%d",&u,&v);
e[cnt]=node(v,head[u]);
head[u]=cnt++;
indegree[v]++;
}
if(topo()) printf("有环
");
return 0;
}
int topo()
{
int i,p,cnt=0;
queue<int> que;
for(i=1;i<=n;i++) //度数为0的点入队列
if(!indegree[i])
que.push(i);
while(!que.empty())
{
cnt++;
p=que.front();
que.pop();
indegree[p]--;
for(i=head[p];i!=-1;i=e[i].next)
{
if(--indegree[e[i].v]==0) //删除度数为0的点和与其相连的边
que.push(e[i].v);
}
}
return cnt==n?0:1;
}
/*
9 11
1 2
1 3
1 4
2 5
3 5
4 6
5 7
5 8
6 8
7 9
8 9
*/
AOE
定义
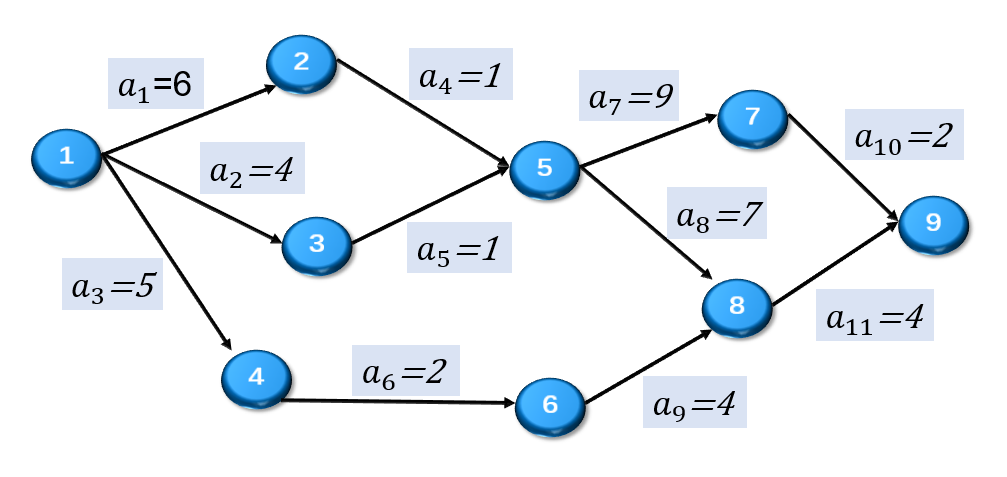
AOE网(Activity On Edge Network)是边表示活动的网,AOE网是带权有向无环图。
用顶点表示事件,用有向边表示活动,边上的权值表示活动的持续时间。由于整个工程只有一个起点和一个终点,网中只有一个入度为0的点(源点)和一个出度为0的点(汇点)。
只有在某顶点所代表的事件发生后,从该顶点出发的各活动才能开始。
只有在进入某顶点的各活动都结束,该顶点所代表的事件才能发生。
解决
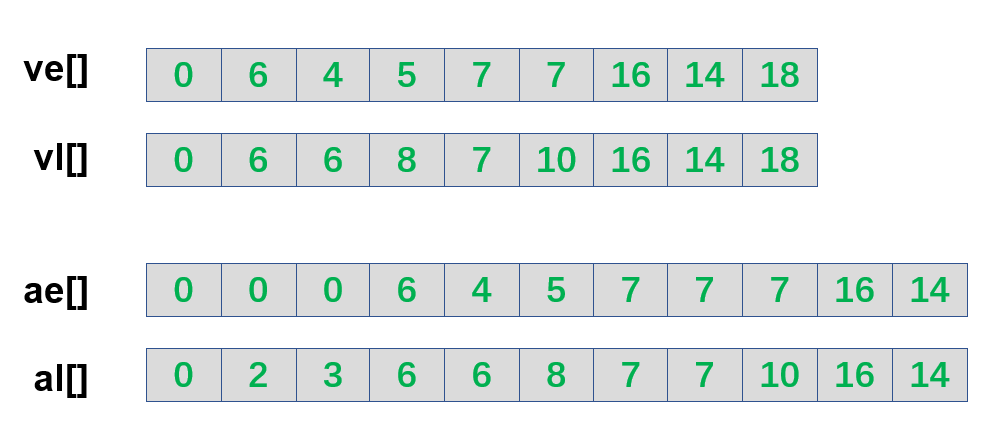
事件最早发生时间ve[k]:
即之前所有活动均完成所需的时间,由耗时最长的路径决定。
事件的最晚发生时间vl[k]:
事件的最晚发生时间以不影响工程最终完成时间为原则。源点(汇点)的最早发生时间和最晚发生时间相同。
对与事件k的最晚发生时间可以采用:汇点的发生时间减去到j的最长路径来求得。(n为汇点)
活动的最早开始时间ae[k]:
活动的的开始时间与事件发生时间相互联系,活动的最早发生时间为其起点事件的最早发生时间。
若,则活动
的最早开始时间应等于事件
的最早发生时间,有 ae[i]=ve[k]。
活动的最晚开始时间al[k]:
活动的最晚开始时间是指,在不推迟整个工期的前提下, ai必须开始的最晚时间。
若,则的
最晚开始时间要保证事件
的最迟发生时间不拖后,有
活动的最晚开始时间为其终点的最晚开始时间减去活动进行的时间。
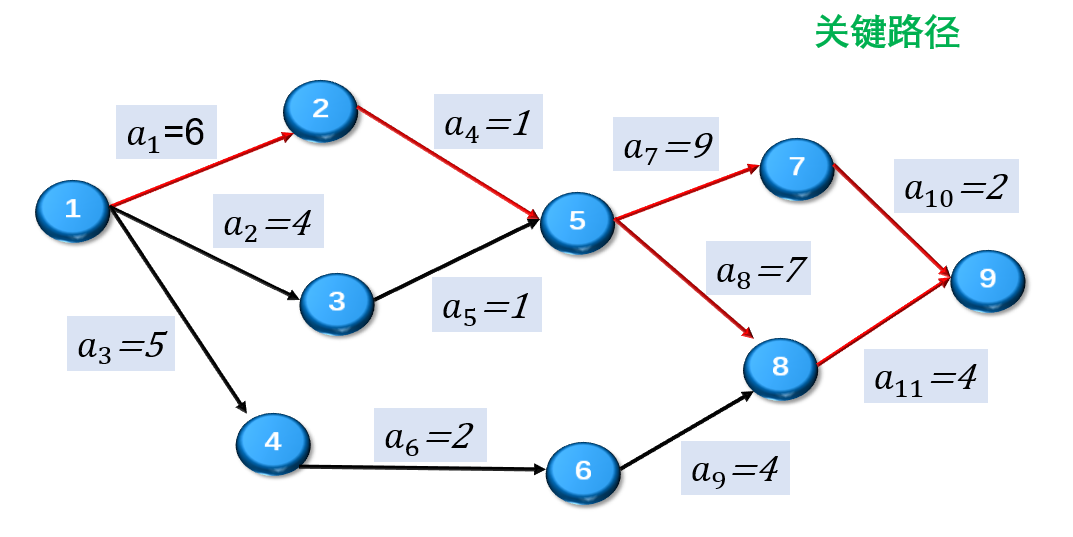
关键路径
在AOE网中,从始点到终点具有最大路径长度(该路径上的各个活动所持续的时间之和)的路径称为关键路径。
关键路径长度是整个工程所需的最短工期。
关键活动
关键路径上的活动称为关键活动(ae[i]=al[i])
由于AOE网中的某些活动能够同时进行,故完成整个工程所必须花费的时间应该为始点到终点的最大路径长度。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=10005;
struct node
{
int v,w,next;
node(){}
node(int a,int b,int c)
{v=a;w=b;next=c;}
}e[maxn],re[maxn];
struct Edge
{
int l,r,w;
Edge(){}
Edge(int a,int b,int c)
{l=a;r=b;w=c;}
}edge[maxn];
int head[maxn],rhead[maxn],indegree[maxn],rindegree[maxn];
int ve[maxn],vl[maxn],ae[maxn],al[maxn],n,m,end;
int topo();
void cal_vl();
void cal_activity();
void print(int ans[],int n);
int main()
{
fill(head,head+maxn,-1);
fill(rhead,rhead+maxn,-1);
fill(vl,vl+maxn,0x7fffffff);
int i,u,v,w,cnt=1,rcnt=1;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[cnt]=node(v,w,head[u]);head[u]=cnt++;indegree[v]++;
re[rcnt]=node(u,w,rhead[v]);rhead[v]=rcnt++;rindegree[u]++;
edge[i]=Edge(u,v,w);
}
if(topo()) {printf("有环
");return 0;}
cal_vl();
cal_activity();
printf("事件的最早发生时间:
");print(ve,n);
printf("
事件的最晚发生时间:
");print(vl,n);
printf("
活动的最早发生时间:
");print(ae,m);
printf("
活动的最晚发生时间:
");print(al,m);
return 0;
}
void print(int ans[],int n)
{
for(int i=1;i<=n;i++)
printf("%d = %d%s",i,ans[i],i==n?"
":" ");
}
int topo()
{
int i,p,cnt=0;
queue<int> que;
for(i=1;i<=n;i++)
if(!indegree[i])
que.push(i);
while(!que.empty())
{
cnt++;
p=que.front();
que.pop();
end=p;
indegree[p]--;
for(i=head[p];i!=-1;i=e[i].next)
{
int v=e[i].v;
if(--indegree[v]==0)
que.push(v);
ve[v]=max(ve[v],ve[p]+e[i].w);
}
}
return cnt==n?0:1;
}
void cal_vl()
{
int i,p;
queue<int> que;
vl[end]=ve[end];
que.push(end);
while(!que.empty())
{
p=que.front();
que.pop();
for(i=rhead[p];i!=-1;i=re[i].next)
{
int v=re[i].v;
vl[v]=min(vl[v],vl[p]-re[i].w);
if(--rindegree[v]==0)
que.push(v);
}
}
}
void cal_activity()
{
int i;
for(i=1;i<=m;i++)
{
ae[i]=ve[edge[i].l];
al[i]=vl[edge[i].r]-edge[i].w;
}
}
/*
9 11
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4
*/
应用
下列AOE 网表示一项包含 8 个活动的工程。通过同时加快若干活动的进度可以缩短整个工程的工期。下列选项中,加快其进度就可以缩短工程工期的是( )。
 A. c 和 e B. d 和 e C.f 和 d D.f 和 h
A. c 和 e B. d 和 e C.f 和 d D.f 和 h
解:
因为关键路径有三条,分别为:
1. b、d、c、g
2. b、d、e、h
3. b、f、h
若想缩短工期,那么加快进度的活动必须覆盖所有关键路径(即所有关键路径中都应该存在加快进度的点),所以选 C 。