辛普森积分入门讲解

辛普森积分

引用部分

• 百度一下

• 文库

定义

辛普森积分法就是在积分区间[a,b]上去找三个点a、b和m=(a+b)/2,计算其原函数的在此处的值,然后用抛物线来拟合原函数。

正文

• Simpson积分公式

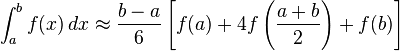
用途:来求一个函数的积分的近似值，用于面积计算等精度要求不是特别苛刻的地方。

其实它就是用一个二次函数曲线不断拟合逼近原函数，然后求得原函数的近似值。

---

• 公式说明:

---

前置：g(x)$g(x)$为一个关于x$x$的二次函数(抛物线)，其中g(x)=A×x2+B×x+C$g(x)=A\times x^2+B\times x+C$，对于求定积分∫x0g(x)dx${\int }_0^{x}g(x)dx$，通过求积得其等于A×x33+B×x22+C×x+D$\frac{A\times x^3}{3}+\frac{B\times x^2}{2}+C\times x+D$ 其中D$D$为常数，可以看做0$0$。令W(x)=∫x0g(x)dx$W(x)={\int }_0^{x}g(x)dx$，所以对于求一段定积分则有∫bag(x)=W(b)−W(a)${\int }_a^{b}g(x)=W(b)-W(a)$。

---

在平面直角坐标系里，由(x1,y1),(x2,y2),(x3,y3)$(x_1,y_1),(x_2,y_2),(x_3,y_3)$(其中x3=x1+x22$x_3=\frac{x_1+x_2}{2}$)确定的抛物线f(x)$f(x)$在区间[x1,x2]的定积分为:

∫x2x1f(x)dx=16×(x2−x1)×(y1+y2+4×y3)$${\int }_{x_1}^{x_2}f(x)dx=\frac{1}{6}\times (x_2-x_1)\times (y_1+y_2+4\times y_3)$$

下面给出简单的证明:

令g(x)=A×x2+B×x+C$g(x)=A\times x^2+B\times x+C$ 为拟合后的抛物线，则有

∫x2x1f(x)dx≈∫x2x1g(x)dx$${\int }_{x_1}^{x_2}f(x)dx\approx {\int }_{x_1}^{x_2}g(x)dx$$

=W(x2)−W(x1)$$=W(x_2)-W(x_1)$$

=A3×(x2)3+B2×(x2)2+C×x2−(A3×(x1)3+B2×(x1)2+C×x1)$$=\frac{A}{3}\times (x_2{)}^3+\frac{B}{2}\times (x_2{)}^2+C\times x_2-\left(\frac{A}{3}\times (x_1{)}^3+\frac{B}{2}\times (x_1{)}^2+C\times x_1\right)$$

=A3×((x2)3−(x1)3)+B2×((x2)2−(x1)2)+C×(x2−x1)$$=\frac{A}{3}\times \left((x_2{)}^3-(x_1{)}^3\right)+\frac{B}{2}\times \left((x_2{)}^2-(x_1{)}^2\right)+C\times (x_2-x_1)$$

=x2−x16×(2×A×((x2)2+x1×x2+(x1)2)+3×B×(x2+x1)+6×C)$$=\frac{x_2-x_1}{6}\times \left(2\times A\times \left((x_2{)}^2+x_1\times x_2+(x_1{)}^2\right)+3\times B\times (x_2+x1)+6\times C\right)$$

展开化简整理得：

=x2−x16×(A×(x1)2+B×x1+C+A×(x2)2+B×x2+C+4×A×(x2+x12)2)$$=\frac{x_2-x_1}{6}\times \left(A\times (x_1{)}^2+B\times x_1+C+A\times (x_2{)}^2+B\times x_2+C+4\times A\times {\left(\frac{x_2+x_1}{2}\right)}^2\right)$$

将其组合成完全平方式(配方)后

=x2−x16×(g(x1)+g(x2)+4×g(x1+x22))$$=\frac{x_2-x_1}{6}\times \left(g(x_1)+g(x_2)+4\times g\left(\frac{x_1+x_2}{2}\right)\right)$$

=x2−x16×(g(x1)+g(x2)+4×g(x3))$$=\frac{x_2-x_1}{6}\times \left(g(x_1)+g(x_2)+4\times g(x_3)\right)$$

于是我们就得到了simpson积分公式

∫baf(x)dx≈b−a6×[g(a)+4×g(a+b2)+g(b)]$${\int }_a^{b}f(x)dx\approx \frac{b-a}{6}\times \left[g(a)+4\times g\left(\frac{a+b}{2}\right)+g(b)\right]$$

在实际计算中g(x)$g(x)$的值可以用原函数f(x)$f(x)$的值来代替，于是就是如下公式:

∫baf(x)dx≈b−a6×[f(a)+4×f(a+b2)+f(b)]$${\int }_a^{b}f(x)dx\approx \frac{b-a}{6}\times \left[f(a)+4\times f\left(\frac{a+b}{2}\right)+f(b)\right]$$

代码：

double simpson(double l,double r){
    return (r-l)*(f(l)+4*f((l+r)/2)+f(r))/6;
}

---

自适应辛普森积分法

• 那么实际程序该如何实现辛普森积分求积呢?

我们如果要求∫baf(x)dx${\int }_a^{b}f(x)dx$的近似值的话，可以用递归二分区间求解来达到要求精度。
用如下公式:

∫baf(x)dx=∫midaf(x)dx+∫bmidf(x)dx$${\int }_a^{b}f(x)dx={\int }_a^{mid}f(x)dx+{\int }_{mid}^{b}f(x)dx$$

其中mid=a+b2$mid=\frac{a+b}{2}$，证明:显然式证明 :)

但是因为是浮点数(小数),那么递归多少层，在什么时候返回值结束递归呢?
我们容易知道如果递归到b−a<eps$b-a<eps$的话精度虽然很高，但是时间复杂度太高了，但是如果递归少了，精度又得不到保证，那该如何是好呢?

• 自适应法

自适应法，就是让程序根据实际情况决定如何运行执行操作。自己随便下的定义而已

这里我们就要用自适应法来解决这个问题啦，让程序自己去决定递归层数，而且又保证精度。

说的很高深，其实很简单。还是比较难吧

• 自动化控制区间分割的大小。

实际操作:二分递归，当满足精度就计算返回值，结束递归。

伪代码:

function(l,r,eps,ans):
mid=(l+r)/2;
lval=左边的值,rval=右边的值;
if (满足精度) return 答案;
eps/=2;
else return 左边递归+右边递归;

注意，这里的ans$ans$表示上一层计算的整个区间的答案，用来和当前这层来判断精度，eps$eps$在递归时每次除以2，这是为了消除精度误差叠加效应，当小误差多了就成大误差了，所以每次要缩小精度。

代码:

double asr(double l,double r,double eps,double ans){
    double mid=(l+r)/2;
    double lval=simpson(l,mid),rval=simpson(mid,r);
    if(fabs(lval+rval-ans)<=15*eps) return lval+rval+(lval+rval-ans)/15;
    return asr(l,mid,eps/2,lval)+asr(mid,r,eps/2,rval);
}
double asme(double a,double b,double eps){
    return asr(a,b,eps,simpson(a,b));
}

推荐文章

---

• 模板1【模板】自适应辛普森法1

代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define db double
using namespace std;
const db eps=1e-7;
db a,b,c,d,L,R;
db f(db x){return (c*x+d)/(a*x+b);}
db simpson(db l,db r){return (f(l)+f(r)+4*f((l+r)/2))*(r-l)/6;}
db asr(db l,db r,db exps,db val){
    db mid=(l+r)/2;
    db lval=simpson(l,mid),rval=simpson(mid,r);
    if(fabs(lval+rval-val)<=15*exps){return lval+rval+(lval+rval-val)/15;}
    return asr(l,mid,exps/2,lval)+asr(mid,r,exps/2,rval);
}
db asme(db l,db r,db exps){return asr(l,r,exps,simpson(l,r));}
int main(){
    scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&L,&R);
    printf("%lf
",asme(L,R,eps));
    return 0;
}

---

• 模板2【模板】自适应辛普森法2

代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define db double
using namespace std;
const db inf=30;
const db eps=1e-7,zero=1e-10;
db a;
db f(db x){return pow(x,a/x-x);}
db simpson(db l,db r){return (f(l)+f(r)+4*f((l+r)/2))*(r-l)/6;}
db asr(db l,db r,db exps,db val){
    db mid=(l+r)/2;
    db lval=simpson(l,mid),rval=simpson(mid,r);
    if(fabs(lval+rval-val)<=15*exps) return lval+rval+(lval+rval-val)/15;
    return asr(l,mid,exps/2,lval)+asr(mid,r,exps/2,rval);
}
db asme(db l,db r,db exps){return asr(l,r,exps,simpson(l,r));}
int main(){
    scanf("%lf",&a);
    if(a<0)puts("orz");
    else printf("%.5lf
",asme(zero,inf,eps));
    return 0;
}

这个虽然求的是不定积分但是，不要被吓到了，因为当x$x$大于30左右后，函数值趋近于0，所以可以不计。
然后当a<0$a<0$时函数不收敛，所以无解。

---

其他题目[NOI2005]月下柠檬树

• simpson的其他用途:

和扫描线结合求圆面积并和其他不规则图形面积等。

【2018.9.7】最近发现的好文章IN