splay的模板以及各种操作的简单实现

splay

一种基于旋转操作的平衡树，所以没法持久化可持久化的去看fhq-treap

关于splay的一些基本操作复杂度正确性证明和实现可以参考网上其他博客，这里就不在详细说明。

一些定义

先简单说明代码中的变量含义：
f[a]表示splay的节点$a$的父亲节点
son[0/1][a]表示splay的节点$a$的左右儿子，$0$为左儿子$1$为右儿子（数组小的一维开在前面可节约寻址时间）。
sze[a]表示splay的节点$a$的子树大小。
tim[a]表示splay的节点$a$所代表的值出现次数。
val[a]表示splay的节点$a$的值
mem[a]废弃节点回收站（省空间用的）
rootsplay的根节点
tot当前总共节点的编号

其中的pushup操作为上传儿子信息更新节点。
一般为

void pushup(int o){
	if(!o)return;
	sze[o]=sze[son[0][o]]+sze[son[1][o]]+tim[o];
}

如果有标记下放的话（比如区间修改的lazy标记），还有pushdown函数。

基本操作：

旋转节点

void rotate(int a,bool k){
	int now=f[a];
	son[k][now]=son[k^1][a];
	f[son[k][now]]=now;
	bool kw=(son[1][f[now]]==now);
	if(f[now])son[kw][f[now]]=a;
	f[a]=f[now];f[now]=a;son[k^1][a]=now;
	pushup(now);pushup(a);
}

将一个点翻转到某个点的儿子处

void splay(int a,int to){
//a->to
	while(f[a]!=to){
		bool k=(son[1][f[a]]==a);
		if(f[f[a]]==to) rotate(a,k);
		else{
			int b=f[a];bool kw=(son[1][f[b]]==b);
			if(son[kw^1][b]==a) rotate(a,k);
			else rotate(b,k);
			rotate(a,kw);
		}
	}
	pushup(a);
	if(!to)root=a;//如果翻转到0号节点的儿子就相当于根节点
}

新建节点

int newnode(int fa,int v){
	int now;
	if(top){//这里使用节点回收方式
		now=mem[top--];
		if(son[0][now])mem[++top]=son[0][now],son[0][now]=0;
		if(son[1][now])mem[++top]=son[1][now],son[1][now]=0;
		tim[now]=1;sze[now]=1;val[now]=v;f[now]=fa;
	}else{//直接新建一个
		now=++tot;
		tim[now]=1;sze[now]=1;val[now]=v;
		f[now]=fa;son[0][now]=son[1][now]=0;
	}//返回当前节点编号
	return now;
}

插入操作

因为splay也是一颗二叉树，满足$lval<oval<rval$，也就是左儿子（子树中）值小于当前节点值小于右（子树中）儿子值，所以插入时，按照大小关系一路走下去，遇到一样的直接计数即可，走到空的了就直接建新节点就好啦。

void insert(int v){
	if(!root){root=newnode(0,v);return;}//当前是空的splay
	int now=root,fa=0;
	while(1){
		//二叉树搜索需要插入在哪里，如果当前节点的值等于插入值，直接计数
		if(val[now]==v){++tim[now];pushup(now);pushup(fa);splay(now,0);break;}
		fa=now;now=son[val[fa]<v][fa];//如果比当前的节点值大去右儿子，小就去左儿子
		if(!now){//空节点
			now=newnode(fa,v);
			son[val[fa]<v][fa]=now;
			pushup(fa);splay(now,0);//splay(now,root)
			//记住每次查询后splay就可以在这里写splay(now,0),splay(now,0)的插入总复杂度为$O(插入节点数)$ 
			//否则不要splay到0，否则超时！！！
			//因为给的是一个递增的序列的话，每次splay到0就会退化成一条链，然后每次询问如果没有splay，也就是翻转操作的话复杂度会退化 
			break;
		}
	}
}

初级操作：

查找某个值的节点编号

按插入的方式走就好啦！

int findnumpos(int num){
	int now=root;
	while(1){
		if(!now) return -1;//没有这个值
		if(val[now]==num){
			splay(now,0);//记得翻转，根据势能分析，这样会使复杂度更优秀
			return now;
		} 
		if(val[now]<num){
			now=son[1][now];
		}else if(val[now]>num){
			now=son[0][now];
		}
	}	
}

查找某个排名的节点编号

查找第$k$个，从根节点往下走，如果左边的节点数大于$k$，直接去左边
否则，减去左边大小，看是否在当前节点内，是就直接返回
否则，减去当前节点大小，去右边。

int findkthpos(int kth){
	int now=root;
	while(1){
		if(!now) return -1;
		if(sze[son[0][now]]>=kth){
			now=son[0][now];//左边
			continue;
		}
		kth-=sze[son[0][now]];//减去左边大小
		if(tim[now]>=kth){//在当前的里面
			splay(now,0);//查询完后splay 
			return now;
		}
		kth-=tim[now];//减去当前大小
		now=son[1][now];//去右边
	}	
}

查找排名第$k$的值

同找编号那个，只不过返回值即可。

int findkth(int kth){
	int now=root;
	while(1){
		if(!now) return -1;
		if(sze[son[0][now]]>=kth){
			now=son[0][now];
			continue;
		}
		kth-=sze[son[0][now]];
		if(tim[now]>=kth){
			splay(now,0);//查询完后splay 
			return val[now];
		}
		kth-=tim[now];
		now=son[1][now];
	}
}

查找某个值的排名

同样的操作，每次走的时候记录前面已经有多少个节点即可。

int findnum(int num){
	int now=root,ans=0;
	while(1){
		if(!now) return -1;//找不到
		if(val[now]==num){
			ans=ans+sze[son[0][now]]+1;//记得+1，当前节点中要算一个
			splay(now,0);
			return ans;//查询完后splay 
		}
		if(val[now]<num){//去右边加上左边的大小
			ans+=sze[son[0][now]]+tim[now];
			now=son[1][now];
		}else if(val[now]>num){
			now=son[0][now];
		}
	}
}

中级操作：

查找前驱

查找一个节点比它小的最大的一个。

将这个数字翻转到根节点，它的左子树内就是所有比它小的点，然后在里面找到最大的一个，也就是一值在里面走右儿子即可（左边的最右边的节点）。

int pre(int x){
	splay(x,0);
	int now=son[0][x];
	if(!now)return val[x];
	while(son[1][now])now=son[1][now];
	return val[now];
}
前驱值

int prepos(int x){
	splay(x,0);
	int now=son[0][x];
	if(!now)return val[x];
	while(son[1][now])now=son[1][now];
	return now;	
}
前驱的节点编号

查找后继

查询比一个节点大的最小的一个。

同样的操作，我们将其翻转到根节点，然后比它大的都在右子树中，在右子树中寻找最小的一个即可，也就是一直走左儿子（右边的最左边的节点）

int nex(int x){
	splay(x,0);
	int now=son[1][x];
	if(!now)return val[x];
	while(son[0][now])now=son[0][now];
	return val[now];
}
后继的值

int nexpos(int x){
	splay(x,0);
	int now=son[1][x];
	if(!now)return val[x];
	while(son[0][now])now=son[0][now];
	return now;	
}
后继节点编号

查找一个值的前驱后继值

一般选择先把这个值插入，然后翻转到根再来查询。

这里没有体现插入（如果有这个值就不用插入了）
int findnumpre(int x){
	x=findnumpos(x);
	return pre(x);
}
int findnumnex(int x){
	x=findnumpos(x);
	return nex(x);
}

查找一个排名为$k$的值的前驱后继值

同理，找到这个节点后就可以去查询了。

int findkthpre(int x){
	x=findkthpos(x);
	return pre(x);
}
int findkthnex(int x){
	x=findkthpos(x);
	return nex(x);
}

高级操作

删除一个节点

对于节点的删除，是比较难写的，分为以下几种情况：

• 先找到要删的节点，然后将其翻转到根节点：

1. 如果没有该节点，不用删，直接跳过。
2. 如果只有根这一个节点，且要删的就是这个，直接删掉即可。
3. 如果该节点只有一个儿子，直接删除该节点，将它的那个儿子作为新的根
4. 如果有两个儿子，先找到该节点的前驱，将其翻转到该节点的左儿子处，由于前驱是比它小的里面最大的一个，所以此时它的左儿子没有右儿子，然后将该点删除，将它的右儿子接到它的左儿子的右儿子处，将它的左儿子作为新的根即可，此时仍然保证了排序二叉树的性质。

void delet(int pos){
	mem[++top]=pos;//回收节点
	son[0][pos]=son[1][pos]=0;f[pos]=0;
	val[pos]=0;sze[pos]=tim[pos]=0;
}//删除一个节点记得删干净，防止对以后造成影响
void delpos(int v){
	splay(v,0);//先翻转到根
	if(tim[v]>1){--tim[v];return;}//有多个直接删一个
	if(!son[0][v]&&!son[1][v]){delet(v);root=0;return;}//只有这个节点直接删除
	int now;
	if(!son[0][v]){//没有左或者右儿子，直接删除，重新赋根
		now=son[1][v];
		delet(v);
		root=now;f[now]=0;
		pushup(now);
		return;
	}else if(!son[1][v]){
		now=son[0][v];
		delet(v);
		root=now;f[now]=0;
		pushup(now);
		return;
	}
	now=prepos(v);//有两个儿子，先找到前驱，翻转到左儿子处（如果要找后继也是同理的）
	splay(now,v);
	int tnow=son[1][v];
	delet(v);//删除节点
	f[now]=0;
	son[1][now]=tnow;f[tnow]=now;
	root=now;//将右子树接过来，重新赋根
	pushup(tnow);pushup(now);	
}
void delnum(int v){
	v=findnumpos(v);
	delpos(v);//删除某个数
}
void delkth(int v){
	v=findkthpos(v);
	delpos(v);//删除某个排名的数
}

单点修改询问操作

询问的话找到即可。

修改的话如果不影响该节点的位置，可以直接找到它修改即可。
否则先删除原来的，将修改后的重新插入即可。

区间修改询问操作

最开始建树时先加入两个边界节点，防止越界。
这里的splay是按照序列下标为比较关键字的排序二叉树。

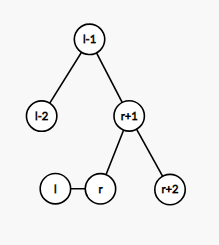
然后对于一个询问区间$lsim r$，我们先将$l-1$翻转到根，然后将$r+1$翻转到$l-1$的右儿子处，就变成如下图：

然后，此时的询问区间$lsim r$已经在$r+1$这个节点的左子树中了，所以直接查询左子树的根节点，也就是$r+1$的左儿子所维护的值即可。

对于区间修改，我们同样进行询问时的操作，然后要维护一个$m lazy$标记，将修改操作更新到此时$r+1$的左儿子的$m lazy$标记上即可。

注意：由于有lazy标记，所以翻转时注意及时下传标记，更新节点，以防止标记传错或者更新不及时。

由于这里我们用到了$l-1$和$r+1$号节点，所以对于节点$1sim n$的，如果查询$1sim n$这个区间，就会用到$0,n+1$这两个节点，所以开始建树时要多加入两个节点。

区间翻转

维护一个$rev[a]$标记，表示是否翻转，每次修改$xor 1$即可，然后要交换的话就先将区间用前面讲的方式提取出来，交换左子树根节点的左右儿子即可。

注意及时下传和更新。

void pushdown(int a){
	if(!rev[a]) return;
	if(son[a][0])rev[son[a][0]]^=1;
	if(son[a][1])rev[son[a][1]]^=1;
	swap(son[a][0],son[a][1]);
	rev[a]=0;
}
void revse(int a,int b){
	splay(a,0);splay(b,a);
	rev[son[b][0]]^=1;
}

---

一些模板题目

1. 【区间翻转】

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int root,n,m;
int son[N][2],f[N],sze[N];
bool rev[N];
void pushup(int a){sze[a]=sze[son[a][0]]+sze[son[a][1]]+1;}
void pushdown(int a){
    if(!rev[a]) return;
    if(son[a][0])rev[son[a][0]]^=1;
    if(son[a][1])rev[son[a][1]]^=1;
    swap(son[a][0],son[a][1]);
    rev[a]=0;
}
void rotate(int a,bool k){
    int now=f[a];
    pushdown(now);pushdown(a);
    son[now][k]=son[a][k^1];
    f[son[now][k]]=now;
    bool dk=(son[f[now]][1]==now);
    if(f[now]) son[f[now]][dk]=a;
    f[a]=f[now];f[now]=a;son[a][k^1]=now;
    pushup(now);pushup(a); 
}
void splay(int a,int to){
    pushdown(a);
    while(f[a]!=to){
        if(f[f[a]]!=to) pushdown(f[f[a]]);
        pushdown(f[a]);pushdown(a);
        bool k=(son[f[a]][1]==a);
        if(f[f[a]]==to){
            rotate(a,k);
        }else{
            int b=f[a];
            bool kw=(son[f[b]][1]==b);
            if(son[b][kw^1]==a) rotate(a,k);
            else rotate(b,k);
            rotate(a,kw);
        }
    }
    pushup(a);
    if(!to)root=a;
}
void revse(int a,int b){
    splay(a,0);splay(b,a);
    rev[son[b][0]]^=1;
}
int find(int a,int kth){
    pushdown(a);
    if(son[a][0]&&sze[son[a][0]]>=kth) return find(son[a][0],kth);
    kth-=sze[son[a][0]];
    if(kth==1) return a;
    --kth;
    if(son[a][1]) return find(son[a][1],kth);
}
void build(int nn){
    root=son[0][0]=son[0][1]=sze[0]=rev[0]=f[0]=0;
    int mid=1+(nn>>1),pos=mid;f[mid]=0;
    son[0][1]=mid;sze[mid]=1;rev[mid]=0;
    for(int i=mid-1;i>=1;i--){
        son[pos][0]=i;sze[i]=1;f[i]=pos;rev[i]=0;
        son[i][0]=son[i][1]=0;pos=i;
    }
    pos=mid;
    for(int i=mid+1;i<=nn;i++){
        son[pos][1]=i;sze[i]=1;f[i]=pos;rev[i]=0;
        son[i][0]=son[i][1]=0;pos=i;
    }
    splay(1,0);splay(nn,0);
}
int tot;
void out(int a){
    if(!a||tot>n) return;
    pushdown(a);
    out(son[a][0]);
    printf("%d ",a-1);
    ++tot;
    out(son[a][1]);
}
void getans(){
    splay(1,0);splay(n+2,1);
    out(son[n+2][0]);
}
int a,b;
int main(){
    scanf("%d%d",&n,&m);
    build(n+2);
    while(m--){
        scanf("%d%d",&a,&b);
        revse(find(root,a),find(root,b+2));
    }
    getans();
    return 0;
}

2. 【平衡树的一些基本操作】

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int M=1e5+10;
int n;
int root,mem[M],tot,top;;
int son[2][M],sze[M],val[M],tim[M],f[M];
void pushup(int o){
    if(!o)return;
    sze[o]=sze[son[0][o]]+sze[son[1][o]]+tim[o];
}
void rotate(int a,bool k){
    int now=f[a];
    son[k][now]=son[k^1][a];
    f[son[k][now]]=now;
    bool kw=(son[1][f[now]]==now);
    if(f[now])son[kw][f[now]]=a;
    f[a]=f[now];f[now]=a;son[k^1][a]=now;
    pushup(now);pushup(a);
}
void splay(int a,int to){
    while(f[a]!=to){
        bool k=(son[1][f[a]]==a);
        if(f[f[a]]==to) rotate(a,k);
        else{
            int b=f[a];bool kw=(son[1][f[b]]==b);
            if(son[kw^1][b]==a) rotate(a,k);
            else rotate(b,k);
            rotate(a,kw);
        }
    }
    pushup(a);
    if(!to)root=a;
}
int newnode(int fa,int v){
    int now;
    if(top){
        now=mem[top--];
        if(son[0][now])mem[++top]=son[0][now],son[0][now]=0;
        if(son[1][now])mem[++top]=son[1][now],son[1][now]=0;
        tim[now]=1;sze[now]=1;val[now]=v;f[now]=fa;
    }else{
        now=++tot;
        tim[now]=1;sze[now]=1;val[now]=v;
        f[now]=fa;son[0][now]=son[1][now]=0;
    }
    return now;
}
void insert(int v){
    if(!root){root=newnode(0,v);return;}
    int now=root,fa=0;
    while(1){
        if(val[now]==v){++tim[now];pushup(now);pushup(fa);splay(now,0);break;}
        fa=now;now=son[val[fa]<v][fa];
        if(!now){
            now=newnode(fa,v);
            son[val[fa]<v][fa]=now;
            pushup(fa);splay(now,0);
            break;
        }
    }
}
int findnumpos(int num){
    int now=root;
    while(1){
        if(!now) return -1;
        if(val[now]==num){
            splay(now,0);
            return now;
        } 
        if(val[now]<num){
            now=son[1][now];
        }else if(val[now]>num){
            now=son[0][now];
        }
    }	
}
int findkthpos(int kth){
    int now=root;
    while(1){
        if(!now) return -1;
        if(sze[son[0][now]]>=kth){
            now=son[0][now];
            continue;
        }
        kth-=sze[son[0][now]];
        if(tim[now]>=kth){
            splay(now,0);
            return val[now];
        }
        kth-=tim[now];
        now=son[1][now];
    }	
}
int findkth(int kth){
    int now=root;
    while(1){
        if(!now) return -1;
        if(sze[son[0][now]]>=kth){
            now=son[0][now];
            continue;
        }
        kth-=sze[son[0][now]];
        if(tim[now]>=kth){
            splay(now,0);
            return val[now];
        }
        kth-=tim[now];
        now=son[1][now];
    }
}
int findnum(int num){
    int now=root,ans=0;
    while(1){
        if(!now) return -1;
        if(val[now]==num){
            ans=ans+sze[son[0][now]]+1;
            splay(now,0);
            return ans; 
        }
        if(val[now]<num){
            ans+=sze[son[0][now]]+tim[now];
            now=son[1][now];
        }else if(val[now]>num){
            now=son[0][now];
        }
    }
}
int pre(int x){
    splay(x,0);
    int now=son[0][x];
    if(!now)return val[x];
    while(son[1][now])now=son[1][now];
    return val[now];
}
int nex(int x){
    splay(x,0);
    int now=son[1][x];
    if(!now)return val[x];
    while(son[0][now])now=son[0][now];
    return val[now];
}
int prepos(int x){
    splay(x,0);
    int now=son[0][x];
    if(!now)return val[x];
    while(son[1][now])now=son[1][now];
    return now;	
}
int nexpos(int x){
    splay(x,0);
    int now=son[1][x];
    if(!now)return val[x];
    while(son[0][now])now=son[0][now];
    return now;	
}
int findnumpre(int x){
    x=findnumpos(x);
    return pre(x);
}
int findnumnex(int x){
    x=findnumpos(x);
    return nex(x);
}
int findkthpre(int x){
    x=findkthpos(x);
    return pre(x);
}
int findkthnex(int x){
    x=findkthpos(x);
    return nex(x);
}
void delet(int pos){
    mem[++top]=pos;
    son[0][pos]=son[1][pos]=0;f[pos]=0;
    val[pos]=0;sze[pos]=tim[pos]=0;
}
void delpos(int v){
    splay(v,0);
    if(tim[v]>1){--tim[v];return;}
    if(!son[0][v]&&!son[1][v]){delet(v);root=0;return;}
    int now;
    if(!son[0][v]){
        now=son[1][v];
        delet(v);
        root=now;f[now]=0;
        pushup(now);
        return;
    }else if(!son[1][v]){
        now=son[0][v];
        delet(v);
        root=now;f[now]=0;
        pushup(now);
        return;
    }
    now=prepos(v);
    splay(now,v);
    int tnow=son[1][v];
    delet(v);
    f[now]=0;
    son[1][now]=tnow;f[tnow]=now;
    root=now;
    pushup(tnow);pushup(now);	
}
void delnum(int v){
    v=findnumpos(v);
    delpos(v);
}
void delkth(int v){
    v=findkthpos(v);
    delpos(v);
}
int opt,x;
int main(){
    scanf("%d",&n);
    while(n--){
        scanf("%d%d",&opt,&x);
        if(opt==1){
            insert(x);
        }else if(opt==2){
            delnum(x);
        }else if(opt==3){
            printf("%d
",findnum(x));
        }else if(opt==4){
            printf("%d
",findkth(x));
        }else if(opt==5){
            insert(x);
            printf("%d
",findnumpre(x));
            delnum(x);
        }else if(opt==6){
            insert(x);
            printf("%d
",findnumnex(x));
            delnum(x);
        }//每次插入再查询
    }
    return 0;
}

---

【参考文章-%%%】
【LCT-也和splay有关系-%%%】