直方图规定化
算法分析
- 求出原图的累积概率分布
- 求出规定图的累积概率分布
- 求出原图中每一个灰度级累积概率与规定图的累积概率最接近的灰度级
- 根据第3步的方法将原图的灰度映射到标准图中距离最近的灰度值
伪代码
function outputimg = my_histspec(A,B)
% 灰度图的直方图规定化
% 输入:A是读入的原图,B是读入的规定化的标准图
% 输出:outputimg是将A规定化到B之后的图像
[HA,WA] = 原图的大小
[HB,WB] = 标准图的大小
统计原图灰度级频数
统计标准图灰度级频数
计算原图灰度级概率
计算标准图灰度级概率
计算原图灰度级累积概率分布
计算标准图灰度级累积概率分布
%求原图和标准图的映射关系,找到两个累积概率最接近的灰度级
遍历原图的每个灰度级
value{j} = 求标准图当前灰度级累积概率与原图所有灰度级累积概率之差的绝对值
[temp{j},index(j)] = index中存的是vlaue中最小值的下标
outputimg = 开辟一个和原图大小一致的新矩阵存放规定化后的图像
遍历outputimg
outputimg(i,j) = 根据映射关系为每一个新矩阵的像素点赋灰度值
转换outputimg成uint8数据类型
end
代码
function outputimg = my_histspec(A,B)
% 灰度图的直方图规定化
% 输入:A是读入的原图,B是读入的规定化的标准图
% 输出:outputimg是将A规定到B之后的图像
[HA,WA] = size(A);
[HB,WB] = size(B);
PA = imhist(A) / (HA * WA);
PB = imhist(B) / (HB * WB);
%求累积概率分布
for i = 2 : 256
PA(i) = PA(i - 1) + PA(i);
PB(i) = PB(i - 1) + PB(i);
end
%求原图和映射图的映射关系,找到两个累积直方图距离最近的点
for j = 1:256
value{j} = abs(PB - PA(j));
[temp{j},index(j)] = min(value{j}) %index中存的是最小值的下标,temp中存的是最小值
end
outputimg = zeros(HA, WA);
for i = 1:HA
for j = 1:WA
outputimg(i,j) = index(A(i,j) + 1)-1;
end
end
outputimg = uint8(outputimg);
end
实验结果
%调用示例:
A = imread('pout.tif');
B = imread('coins.png');
C = my_histspec(A,B);
subplot(2,3,1);imshow(A);title('原图');
subplot(2,3,2);imshow(B);title('标准图');
subplot(2,3,3);imshow(C);title('匹配到标准图后');
subplot(2,3,4);imhist(A);title('原图直方图');
subplot(2,3,5);imhist(B);title('标准图直方图');
subplot(2,3,6);imhist(C);title('匹配到标准图后直方图');
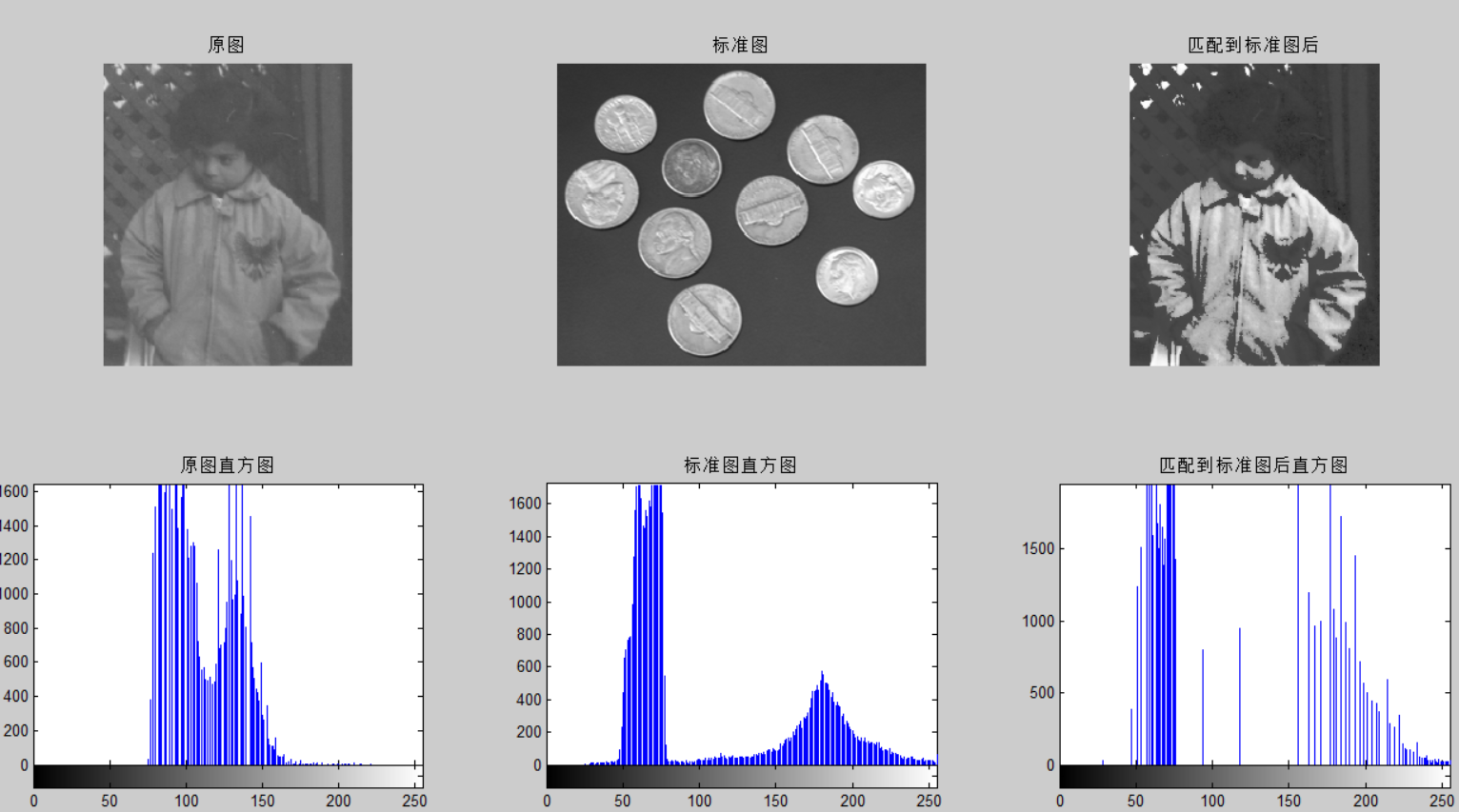
实验分析
- 直方图均衡化是直方图规定化的特例,理想状态下原图直方图均衡化和标准图均衡化后对应的直方图应该是相等的,通过求得原图累积概率和标准图累积概率最接近的灰度值映射,最后的效果是原图的直方图和标准图的直方图接近
