hdu 1757 A Simple Math Problem（矩阵快速幂乘法）

Problem Description

Lele now is thinking about a simple function f(x).

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

Input

The problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.

Output

For each case, output f(k) % m in one line.

 

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

 

Sample Output

45 
104

 

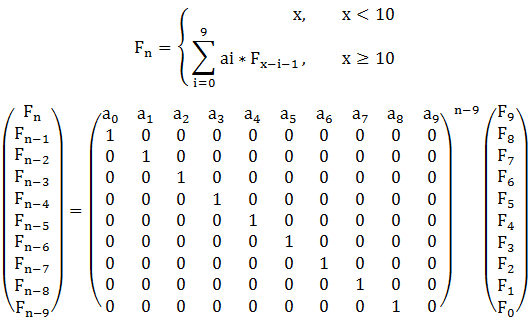
把问题转化为求矩阵的n-9次幂就行了；

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int k,MOD;
int a[10];
int f[10];
struct Matrix
{
    int m[10][10];
}matrix;

Matrix Mul(Matrix a,Matrix b)
{
    Matrix res;
    int i,j,k;
    for(i=0;i<10;i++)
    {
        for(j=0;j<10;j++)
        {
            res.m[i][j] = 0;
            for(k=0;k<10;k++)
                res.m[i][j] = (res.m[i][j]+(a.m[i][k]*b.m[k][j]))%MOD;
        }
    }
    return res;
}

Matrix fastm(Matrix a,int b)
{
    Matrix res;
    memset(res.m,0,sizeof(res.m));
        for(int i=0;i<10;i++)
            res.m[i][i] = 1;
    while(b)
    {
        if(b&1)
            res = Mul(res,a);
        a = Mul(a,a);
        b >>= 1;
    }
    return res;
}
void init()
{
    for(int i=0;i<=9;i++)
    {
        f[i]=i;
    }
}
int main()
{
    init();
    while(scanf("%d%d",&k,&MOD)==2)
    {
        for(int i=0;i<=9;i++)
        {
            scanf("%d",&a[i]);
        }
        if(k<10)
        {
            printf("%d
",k%MOD);
            continue;
        }
        
        memset(matrix.m,0,sizeof(matrix.m));
        for(int i=0;i<=9;i++)
          matrix.m[0][i]=a[i];
        for(int i=1;i<=9;i++)
            matrix.m[i][i-1] = 1;
        Matrix ans=fastm(matrix,k-9);
        Matrix cnt;
        for(int i=0;i<10;i++)
        {
            cnt.m[i][0]=f[9-i];
        }
        Matrix p=Mul(ans,cnt);
        printf("%d
",p.m[0][0]%MOD);
    }
    return 0;
}