jQuery火箭图标返回顶部代码

1)克鲁斯卡尔算法

普里姆算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树。

克鲁斯卡尔算法是直接以边为目标去构建。

因为权值是在边上，直接去找最小权值的边来构建生成树也是很自然的想法，只不过构建时要考虑是否会形成环路而已。

此时我们用到了图的存储结构中的边集数组结构。

以下是边集数组结构的定义代码：

typedef struct
{
    int begin;                         //边的起点的下标
    int end;                           //边的终点的下标
    int weight;                        //边的权值
}Edge;

本算法所用同普里姆算法的实例，我们直接创建图的边集数组。

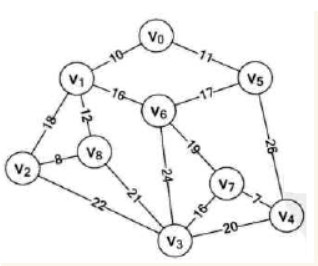
并对边的权值从小到大排序后如下图:

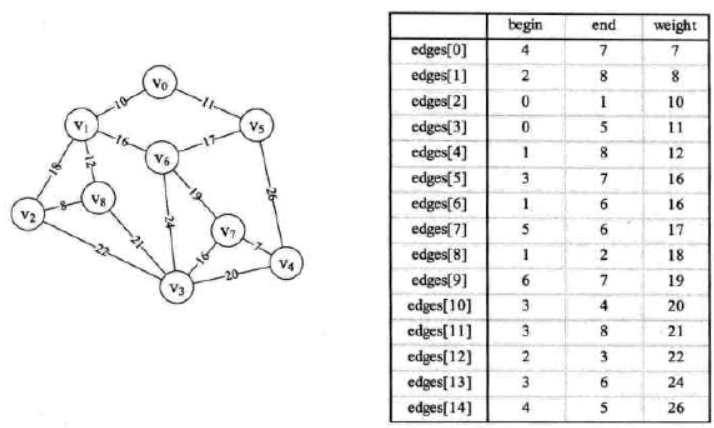
重点分析:

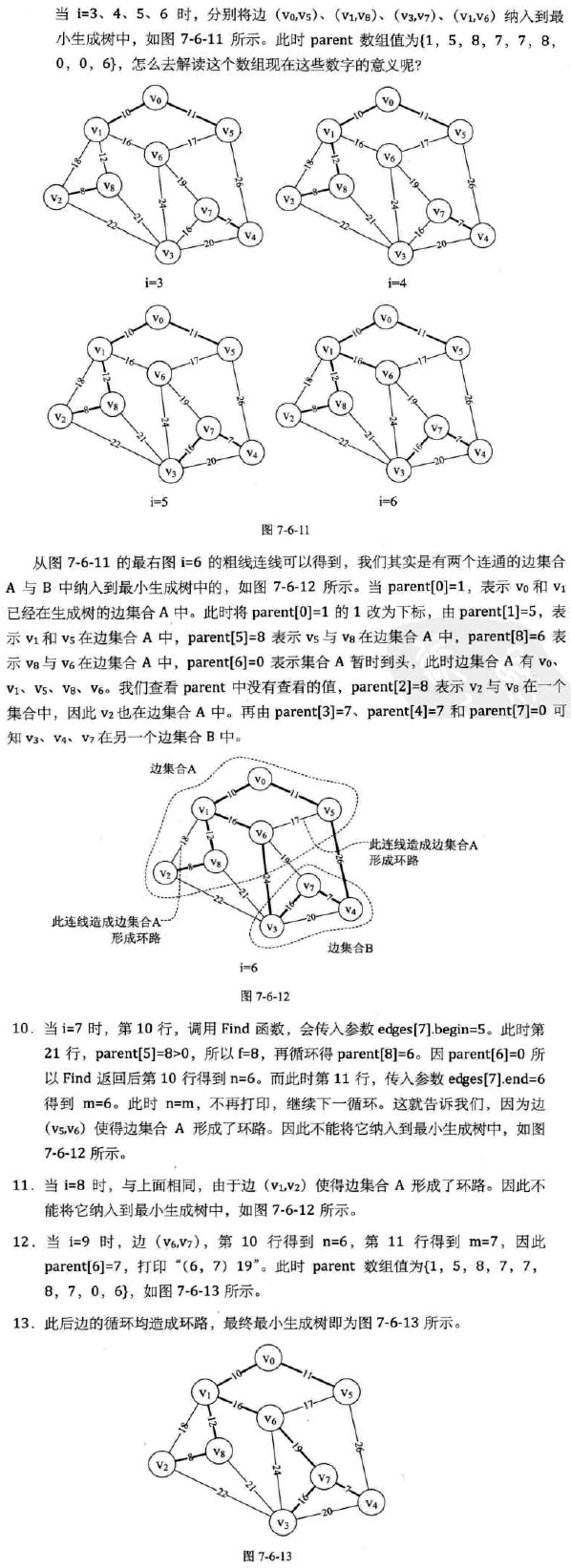
克鲁斯卡尔算法主要针对边展开，边数少时效率会很高，所以对于稀疏图有优势

而普利姆算法对于稠密图，即边数非常多的情况会好些。

代码实现如下:

#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;
typedef struct MGraph
{
    string vexs[60];                   //存放顶点
    int arcs[100][100];                //存放邻接矩阵矩阵
    int vexnum, arcum;                 //总顶点数以及总边数
}MGraph;
typedef struct
{
    int begin;                         //边的起点的下标
    int end;                           //边的终点的下标
    int weight;                        //边的权值
}Edge;

int locateVex(MGraph G, string u)      //找到则返回i，否则返回-1
{
    for (int i = 0; i < G.vexnum; i++)
        if (G.vexs[i] == u)
            return i;
    return -1;
}

void CreateGraphUDG(MGraph &G)         //构造无向图
{
    string v1, v2;                     //两个顶点信息
    int w;                             //两顶点间边的权值
    int i, j, k;
    cout << "请输入顶点数和边数:";
    cin >> G.vexnum >> G.arcum;

    cout << "请输入顶点:";
    for (i = 0; i < G.vexnum; i++)
        cin >> G.vexs[i];

    for (i = 0; i < G.vexnum; i++)     //先将邻接矩阵中所有元素都设为无穷大，这里默认10000为无穷大
        for (j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = 10000;

    cout << "请输入边和权值:" << endl;
    for (k = 0; k < G.arcum; k++)
    {
        cin >> v1 >> v2 >> w;
        i = locateVex(G, v1);
        j = locateVex(G, v2);
        G.arcs[i][j] = G.arcs[j][i] = w;//关于主对角线对称的元素是相等的
    }

}

int cmp(const void* a, const void* b) 
{
    return (*(Edge*)a).weight - (*(Edge*)b).weight;
}

int Find(int *parent, int f)           //查找连接顶点的尾部下标  
{
    while (parent[f] > 0) 
        f = parent[f];
    return f;
}

void MiniSpanTree_Kruskal(MGraph G) 
{
    int i, j, n, m;
    int k = 0;
    int parent[100];                   //用于寻找根节点的数组   
    Edge edges[100];                   //定义边集数组,edge的结构为begin,end,weight,均为整型  
    for (i = 0; i < G.vexnum - 1; i++) // 用来构建边集数组并排序(将邻接矩阵的对角线右边的部分存入边集数组中)  
    {
        for (j = i + 1; j < G.vexnum; j++) 
        {
            if (G.arcs[i][j] < 10000) 
            {
                edges[k].begin = i;    //编号较小的结点为首 
                edges[k].end = j;      //编号较大的结点为尾  
                edges[k].weight = G.arcs[i][j];
                k++;
            }
        }
    }
    qsort(edges, G.arcum, sizeof(Edge), cmp);//为边集数组Edge排序  

    for (i = 0; i < G.vexnum; i++)
        parent[i] = 0;

    cout << "打印最小生成树:" << endl;
    for (i = 0; i < G.arcum; i++) 
    {
        n = Find(parent, edges[i].begin); //寻找边edge[i]的“首节点”所在树的树根  
        m = Find(parent, edges[i].end);   //寻找边edge[i]的“尾节点”所在树的树根
        if (n != m)                       //假如n与m不等，说明两个顶点不在一棵树内，因此这条边的加入不会使已经选择的边集产生回路
        {
            parent[n] = m;                //将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中
            cout << G.vexs[edges[i].begin] << "-" <<G.vexs[ edges[i].end] << " " << edges[i].weight << endl;
        }
    }
}

int main()
{
    MGraph G;
    CreateGraphUDG(G);
    MiniSpanTree_Kruskal(G);
    cout << endl;
    return 0;
}

输出结果: