3996: [TJOI2015]线性代数
Time Limit: 10 SecDescription
给出一个N*N的矩阵B和一个1*N的矩阵C。求出一个1*N的01矩阵A.使得
D=(A*B-C)*A^T最大。其中A^T为A的转置。输出D
Input
第一行输入一个整数N,接下来N行输入B矩阵,第i行第J个数字代表Bij.
接下来一行输入N个整数,代表矩阵C。矩阵B和矩阵C中每个数字都是不超过1000的非负整数。
Output
输出最大的D
Sample Input
3
1 2 1
3 1 0
1 2 3
2 3 7
1 2 1
3 1 0
1 2 3
2 3 7
Sample Output
2
HINT
1<=N<=500
【题解】
花了好久时间化简,最后化简出来是
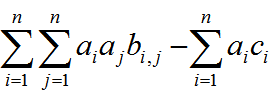
我们发现,a是一个01矩阵,然后其实就可以化成这么一个问题:
有n个东西,选了i,j两件东西能得到b[i,j]的价值,然而选i需要c[i]的花费,选j需要c[j]的花费……
据大聚聚们说,这是一个经典的最小割模型。
建立S,T。
S连(i,j)边,边权为b[i,j],(i,j)连i、连j边,边权均为∞,i向T连边,边权为c[i]。
然后求最小割,最后答案就是
sum(b[i][j])-最小割答案 (i∈[1..n],j∈[1..n])
最小割今天早上刚写过dinic哈哈=-=
然而第一次写边链表,好在也AC了
STL的queue被卡RE了(后来发现并没有) TAT好可怕要自己写队列了
然后了一堆地方有bug调了一个小时

1 #include<iostream> 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<string.h> 5 #include<algorithm> 6 #include<math.h> 7 #include<string> 8 using namespace std; 9 const int inf=210000; 10 int c[250510],head[250510]; 11 long long ans; 12 int q[250510]; 13 int s,t,n,tt,heads,tail; 14 struct edge { 15 int next,num,x; 16 }e[2505010]; 17 int read2() { 18 int x=0; int f=1; 19 char ch=getchar(); 20 while(ch<'0'||ch>'9') {if(ch=='-') f=-1; ch=getchar();} 21 while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0'; ch=getchar();} 22 return x*f; 23 } 24 inline void f(int a,int b,int w) { 25 e[++tt].next=head[a];head[a]=tt; 26 e[tt].num=w;e[tt].x=b; 27 e[++tt].next=head[b];head[b]=tt; 28 e[tt].num=0;e[tt].x=a; 29 } 30 bool bfs() { 31 for (int i=s;i<=t;++i) c[i]=0; 32 heads=tail=1; 33 q[tail]=s;c[s]=1; 34 while(heads<=tail) { 35 int top=q[heads++]; 36 for (int i=head[top];i;i=e[i].next) { 37 int x=e[i].x,num=e[i].num; 38 if(num==0||c[x]>0) continue; 39 c[x]=c[top]+1; 40 q[++tail]=x; 41 if(x==t) return 1; 42 } 43 } 44 return 0; 45 } 46 int dfs(int y,int low) { 47 if(y==t) return low; 48 int flow,r=low; 49 for (int i=head[y];i;i=e[i].next) { 50 int x=e[i].x,num=e[i].num; 51 if(c[x]!=c[y]+1 || num==0) continue; 52 flow=dfs(x,min(r,num)); 53 r-=flow; 54 e[i].num-=flow; e[i^1].num+=flow; 55 if(!r) return low; 56 } 57 if(r==low) c[y]=-1; 58 return low-r; 59 } 60 int main() { 61 //freopen("algebra.in","r",stdin); 62 //freopen("algebra.out","w",stdout); 63 int k,w; 64 n=read2();s=0,t=n*n+n+1; k=n; 65 for (int i=1;i<=n;++i) 66 for (int j=1;j<=n;++j) { 67 w=read2(); 68 ans+=w; 69 f(s,++k,w); 70 f(k,i,inf); 71 f(k,j,inf); 72 } 73 for (int i=1;i<=n;++i) { 74 w=read2(); 75 f(i,t,w); 76 } 77 while(bfs()) ans-=dfs(s,inf); 78 cout<<ans<<endl; 79 //fclose(stdin); 80 //fclose(stdout); 81 return 0; 82 }
wyh大聚聚的代码:300ms比我快多了TAT

1 #include<iostream> 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<string.h> 5 #include<math.h> 6 #include<algorithm> 7 #include<queue> 8 #include<set> 9 #include<map> 10 #include<bitset> 11 #include<vector> 12 using namespace std; 13 #define PA pair<int,int> 14 const int N=0,M=0; 15 inline int read() 16 {int s=0,f=1;char ch=getchar(); 17 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 18 while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+ch-'0';ch=getchar();} 19 return s*f; 20 } 21 int n,np,x[505][505],S,T,h[505][505],d[130005];long long ans; 22 int be[130005],bv[2000005],bl[2000005],bn[2000005],bw=1; 23 void put(int u,int v,int l) 24 {++bw;bn[bw]=be[u];be[u]=bw;bv[bw]=v;bl[bw]=l;} 25 void in() 26 {scanf("%d",&n); 27 for(int i=1;i<=n;i++) 28 for(int j=1;j<=n;j++) 29 {int s=read(); 30 x[max(i,j)][min(i,j)]+=s; 31 if(i!=j)ans+=s; 32 } 33 for(int i=1;i<=n;i++) 34 for(int j=1;j<=i;j++) 35 h[i][j]=++np; 36 S=++np,T=++np; 37 for(int i=1;i<=n;i++) 38 {x[i][i]-=read(); 39 if(x[i][i]>0)ans+=x[i][i]; 40 else put(S,h[i][i],x[i][i]*-1),put(h[i][i],S,0); 41 } 42 for(int i=1;i<=n;i++) 43 {for(int j=1;j<i;j++) 44 put(h[i][i],h[i][j],min(x[i][i]*-1,x[i][j])),put(h[i][j],h[i][i],0); 45 for(int j=i+1;j<=n;j++) 46 put(h[i][i],h[j][i],min(x[i][i]*-1,x[j][i])),put(h[j][i],h[i][i],0); 47 } 48 for(int i=1;i<=n;i++) 49 for(int j=1;j<i;j++) 50 if(x[i][j]) 51 put(h[i][j],T,x[i][j]),put(T,h[i][j],0); 52 } 53 int dfs(int x,int sum) 54 { 55 if(x==T)return sum; 56 int ans=0,f=0; 57 for(int i=be[x];i;i=bn[i]) 58 if(bl[i]) 59 if(d[bv[i]]==d[x]+1) 60 {f=dfs(bv[i],min(sum,bl[i])); 61 ans+=f; 62 sum-=f; 63 bl[i]-=f; 64 bl[i^1]+=f; 65 if(!sum)return ans; 66 } 67 return ans; 68 } 69 queue<int>q; 70 int bfs() 71 {q.push(S); 72 for(int i=1;i<=np;i++) 73 d[i]=5000000; 74 d[S]=1;q.push(S); 75 while(!q.empty()) 76 {int u=q.front();q.pop(); 77 for(int i=be[u];i;i=bn[i]) 78 if(d[bv[i]]>d[u]+1&&bl[i]) 79 {d[bv[i]]=d[u]+1; 80 q.push(bv[i]); 81 } 82 } 83 return dfs(S,500000); 84 } 85 int main() 86 { 87 freopen("algebra.in","r",stdin); 88 freopen("algebra.out","w",stdout); 89 in(); 90 int s=0; 91 while(s=bfs())ans-=s; 92 printf("%d",ans); 93 return 0; 94 }
这是我在BZOJ AC的第10题,仅此纪念 2015/6/12
