翻译: How to do Deep Learning on Graphs with Graph Convolutional Networks
什么是图卷积网络
图卷积网络是一个在图上进行操作的神经网络。给定一个图(G=(E,V)) ,一个GCN的输入包括:
- 一个输入特征矩阵X,其维度是(N imes F^0) ,其中N是节点的数目,(F^0)是每个节点输入特征的数目
- 一个(N imes N)的对于图结构的表示的矩阵,例如G的邻接矩阵A
GCN的一个隐藏层可以写成(H^i=f(H^{i-1},A)),其中(H^0=X)并且(f)是一个propagation。每层(H^i)对应一个(N imes F^i)的特征矩阵,矩阵的每行是一个节点的特征表示。在每层,这些特征通过propagation rule f 聚合起来形成下一层的特征。通过这种方式,特征变得越来越抽象在每一层。在这个框架中,GCN的各种变体仅仅是在propagation rule f 的选择上有不同。
一个简单的 Propagation Rule
一个可能最简单的传播规则是:
(f(H^{i},A)=sigma(AH^iW^i))
其中(W^i)是第i层的权重并且(sigma)是一个非线性激活函数例如ReLU函数。权重矩阵的维度是(F^i imes F^{i+1});也就是说权重矩阵的第二个维度决定了在下一层的特征的数目。如果你对卷积神经网络熟悉,这个操作类似于 filtering operation 因为这些权重被图上节点共享。
简化
让我们在简单的水平上研究 propagation rule 。令:
- (i=1,space s.t. space f)是一个输入特征矩阵的函数,
- (sigma)是恒等函数(Identity function),并且
- 选择权重矩阵满足(AH^0W^0=AXW^0=AX)
也就是说,(f(X,A)=AX)。这个传播规则或许太过简单,但是后面我们将会对缺失的部分进行补充。做个旁注,(AX) 现在等于一个多层感知机的输入层。
一个简单的例子
我们将使用下面的图作为一个简单的例子:
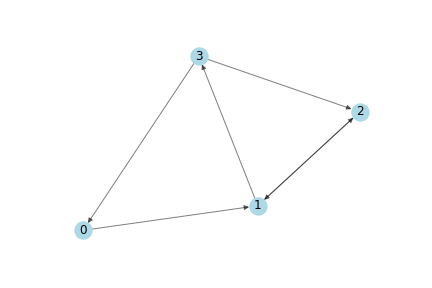
这个图的邻接矩阵表示是
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
接下来,我们需要特征!我们根据每个节点的索引来生成两个整数特征。这会使得后面手动验证矩阵的计算过程更容易。
X = np.matrix([
[i, -i]
for i in range(A.shape[0])
], dtype=float)
使用 Propagation Rule
好了,现在我们有了一个图,以及它的邻接矩阵A和一个输入特征的集合X。让我们看看当使用传播规则时会发生什么:
In [6]: A * X
Out[6]: matrix([
[ 1., -1.],
[ 5., -5.],
[ 1., -1.],
[ 2., -2.]]
发生了什么,每个节点的表示(每一行)现在等于他的邻居的特征的和!换句话说,图卷积层将每个节点表示成它的邻居的总数。在手动验证的时候注意,一个节点 n 是一个节点 v 的邻居只有在存在一个从 v 到 n 的边时。
即将出现的问题
你可能已经注意到了问题:
- 一个节点的聚集表示不包括它自己的特征!这个表示只是它的邻居节点特征的聚集,所以只有有一个自循环的节点才会包括它自己的特征在聚集中。
- 具有很大度数的节点将会有很大的值在它们的特征表示中,而具有很小度数的节点将会有很小的值。这些可能造成梯度消失或者梯度爆炸。这对于随机梯度下降也可能是有问题的,随机梯度下降通常被用来训练这样的网络,而且对于每个输入特征的值的范围是敏感的。
下面,我将分别讨论这些问题
加入 Self-Loops
为了处理第一个问题,我们可以通过简单地给每个节点加入一个自循环。在实践中,这可以通过把单位矩阵 I 加到邻接矩阵 A (在应用传播规则之前)上来实现。
I = np.matrix(np.eye(A.shape[0]))
A_hat = A + I
In [8]: A_hat = A + I
A_hat * X
Out[8]: matrix([
[ 1., -1.],
[ 6., -6.],
[ 3., -3.],
[ 5., -5.]])
因为现在每个节点是自己的邻居,所以节点在计算邻居节点的特征之和的过程中也把自己的特征加进去了。
Normalizing the Feature Representations
特征表示可以通过节点的度来进行归一化,方法是将邻接矩阵 A 转换为 A 和度矩阵D的逆的乘积。因此我们简化的传播规则看起来向这样:
(f(X,A) = D^{-1}AX)
让我们看看发生了什么。首先我们计算度矩阵
D = np.array(np.sum(A,axis=0))[0]
D = np.matrix(np.diag(D))
In [9]: D
Out[9]: matrix([
[1., 0., 0., 0.],
[0., 2., 0., 0.],
[0., 0., 2., 0.],
[0., 0., 0., 1.]
])
在我们应用规则之前,让我们看看在转换了邻接矩阵后,其上发生了什么。
转换前
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
转换后
In [10]: D**-1 * A
Out[10]: matrix([
[0. , 1. , 0. , 0. ],
[0. , 0. , 0.5, 0.5],
[0. , 0.5, 0. , 0. ],
[1. , 0. , 1. , 0. ]
])
注意到邻接矩阵每行的权重在原来权重的基础上除以对应行的节点的度数。我们在变化后的邻接矩阵上应用传播规则:
In [11]: D**-1 * A * X
Out[11]: matrix([
[ 1. , -1. ],
[ 2.5, -2.5],
[ 0.5, -0.5],
[ 2. , -2. ]
])
我们将邻居节点特征均值作为节点的表示。
总结
我们现在把自循环和归一化技巧结合起来。另外,我们将再次引入权重和激活函数(这在前面为了简化讨论而省略了)。
加入权重
首先第一件事是应用权重。注意到这里 D_hat 是矩阵 A_hat = A + I 的度矩阵。
In [45]: W = np.matrix([
[1, -1],
[-1, 1]
])
D_hat**-1 * A_hat * X * W
Out[45]: matrix([
[ 1., -1.],
[ 4., -4.],
[ 2., -2.],
[ 5., -5.]
])
如果我们想要减少输出特征表示的维度,我们可以减少权重矩阵的规模:
In [46]: W = np.matrix([
[1],
[-1]
])
D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
[4.],
[2.],
[5.]]
)
加入激活函数
我们选择保持特征表示的维度并且应用ReLU激活函数。
In [51]: W = np.matrix([
[1, -1],
[-1, 1]
])
relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]])
这就是一个带有邻接矩阵,输入特征,权重和激活函数的完整的隐藏层。
回到现实
最后,我们在一个真实的图上应用一个图卷积网络。我将会告诉你怎样去产生特征表示就像我们前面讲的。
Zachary's Karate Club
Zachary's Karate Club 是一个广泛使用的社交网络。其中的节点表示一个空手道俱乐部的成员,而边表示相互之间的关系。当Zachary在研究空手道俱乐部时,在管理员和教员之间产生了矛盾,这使得俱乐部分成了两个部分。下面的图展示了网络的图表示并且节点根据各自的派别作了标记。管理员和教员分别标记为'A' 和 'I'。
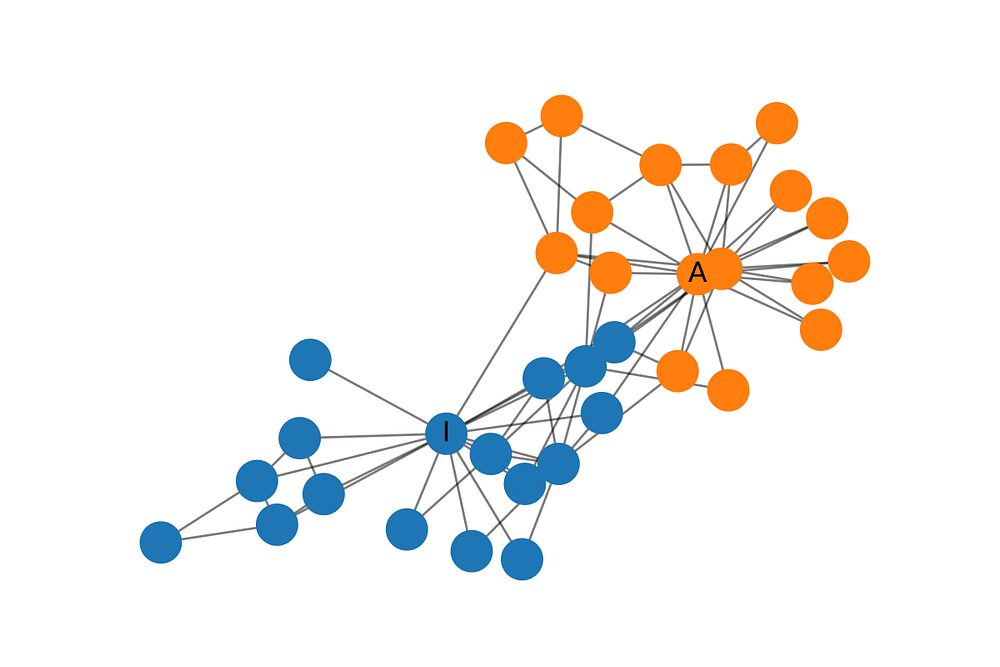
构建GCN
现在让我们来建立图卷积网络。事实上我们将不会训练这个网络,而是简单地进行随机初始化来产生特征表示。