一、 排序的基本概念和分类
- 1. 排序的定义
排序:排序是将一批无序的记录(数据)重新排列成按关键字有序的记录序列的过程。
排序通常是对于记录来说的,将一组记录按照某个关键字排成递增有序(递减有序)。在现实生活照中排序也经常用到,比如站队的时候按照身高由低到高排序。
- 2. 排序的分类
排序的分类:排序分为插入排序、选择排序、交换排序、归并排序四大类,详细分类如下图16-1所示。

- 1. 排序的稳定性
稳定排序:对于关键字相等的记录,排序前后相对位置不变。
不稳定排序:对于关键字相等的记录,排序前后相对位置可能发生变化。
一、 内排序与外排序
待排序的记录数量不同,排序过程中涉及的存储器的不同,有不同的排序分类。
待排序的记录数不太多:所有的记录都能存放在内存中进行排序,称为内部排序;
待排序的记录数太多:所有的记录不可能存放在内存中, 排序过程中必须在内、外存之间进行数据交换,这样的排序称为外部排序。
二、 直接插入排序
- 1. 直接插入排序思想:
将待排序的记录Ri,插入到已排好序的记录表R1, R2 ,…., Ri-1中,得到一个新的、记录数增加1的有序表。 直到所有的记录都插入完为止。
设待排序的记录顺序存放在数组R[1…n]中,在排序的某一时刻,将记录序列分成两部分:
◆ R[1…i-1]:已排好序的有序部分;
◆ R[i…n]:未排好序的无序部分。
显然,在刚开始排序时,R[1]是已经排好序的。
- 2. 直接插入排序算法
例题: 关键字序列T=(13,6,3,31,9,27,5,11),其直接插入排序的排序过程如下:
【13】, 6, 3, 31, 9, 27, 5, 11
第1趟排序: 【6, 13】, 3, 31, 9, 27, 5, 11
第2趟排序: 【3, 6, 13】, 31, 9, 27, 5, 11
第3趟排序: 【3, 6, 13,31】, 9, 27, 5, 11
第4趟排序: 【3, 6, 9, 13,31】, 27, 5, 11
第5趟排序: 【3, 6, 9, 13,27, 31】, 5, 11
第6趟排序: 【3, 5, 6, 9, 13,27, 31】, 11
第7趟排序: 【3, 5, 6, 9, 11,13,27, 31】
算法:
#define N 8 int i,j,t,a[N]={ 13,6,3,31,9,27,5,11}; for(i=1;i<N;i++) //从第2个记录到最后一个逐一前插 { t=a[i]; if(t<a[i-1]) { for(j=i-1;j>=0&&a[j]>t;j--) //只要有序序列比t大,记录后移 { a[j+1]=a[j]; } a[j+1]=t; //将t插入在比它小的元素的后面 } }
- 1. 直接插入排序复杂度分析
(1) 最好情况:若待排序记录按关键字从小到大排列(正序),算法中的内循环无须执行,则一趟排序时:关键字比较次数1次,每趟排序都要移动将近1个记录,这样n个记录最终的时间复杂度是O(n)。
(2) 最坏情况:若待排序记录按关键字从大到小排列(逆序),n个记录需要n-1趟排序,最坏的情况就是完全逆序的情况,每趟排序都要移动将近n个记录,这样最终的时间复杂度是O(n2)。
(3) 稳定性:稳定排序
一、 希尔排序的原理
希尔排序(Shell Sort)又称“缩小增量排序”(Diminishing Increment Sort),它也是一种属于插入排序类的方法,但在时间效率上较前几种排序方法有较大的改进。
从对直接插入排序的时间复杂度的分析得知,其时间复杂度是O(n2),待排记录是正序时,可提高到O(n)。当记录基本有序时,会大大提高效率。而希尔排序正是对直接插入排序进行改进得到的一种插入排序方法。
基本思想是:先将整个待排记录分割成若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
二、 希尔排序的过程
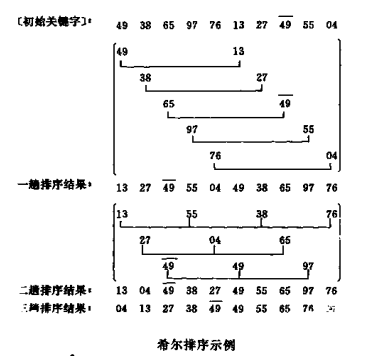
以(49 38 65 97 76 13 27 49 55 04)关键字为例,先看一下希尔排序的过程。初始关键字如图的第一行所示。首先将该序列分成五个子序列{R1,R6},{R2,R7},...{R5,R10},如图的第二行至第六行所示,分别对每个子序列进行直接插入排序,排序结果如图第七行所示,从第一行的初始序列得到第七列的序列的过程称为一趟希尔排序。然后进行第二趟希尔排序,即对下列三个子序列:{R1,R4,R7,R10},{R2,R5,R8},{R3,R6,R9}进行直接插入排序,其结果如图第十一行所示,最后对整个序列进行一趟直接插入排序。至此,希尔排序结束,整个序列的记录已按关键字非递减有序排列
一、 希尔排序的算法
从上述排序过程可见,希尔排序的一个特点是:子序列的构成不是简单地“逐段分割”而是将相隔某个“增量”的记录组成子序列。如上例中,第一趟排序时的增量为5,第二趟排序时的增量为3,由于在前两趟的插入排序中记录的关键字是和同一子序列中的前一个记录的关键字进行比较,因此关键字较小的记录就不是一步一步的往前挪动,而是跳跃式的往前移。,从而使得在最后一趟增量为1时的插入排序时,序列已基本有序,只要做记录的少量比较和移动即可完成排序,因此希尔排序比直接插入排序的时间复杂度低。算法如下:
void shell(int a[],int n)//希尔排序 { int i,j,k,t; k=n/2; //增量k,并逐步缩小增量 while(k>=1) { for(i=k;i<n;i++) //从第gap个元素,逐个对其所在组进行直接插入排序操作 { t=a[i]; j=i-k; while((a[j]>t)&&(j>=0)) //移动法 { a[j+k]=a[j]; j=j-k; } a[j+k]=t; //插入 } k=k/2; } printf("输出希尔排序的结果: "); for(i=0;i<n;i++) { printf("%d ",a[i]); } } void main() { int a[]={15,14,13,12,11,9,8,6,7,5}; shell(a,sizeof(a)/sizeof(int)); }

一、 希尔排序的时间复杂度分析
希尔排序的分析是一个复杂的问题,因为它的时间是所取“增量”序列的函数,这涉及一些数学上尚未解决的难题。因此到目前为止尚未有人求得一种最好的增量序列,但大量的研究已得出一些局部的结论。有人指出,当增量序列为dlta[k]=2t-k+1-1时,希尔排序的时间复杂度为O(n3/2),其中t为排序趟数,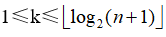
代码希尔排序
/* 希尔排序 缩小增量排序----->通俗的讲就是改进后的直接插入排序 增加了k 增量序列 分组的组数 k=MAX/2 增量k的值是越来越小 先分小组,分别对每个组内进行直接插入排序 然后在k=k/2 分组 直到组数为1截止 进行最终的一趟直接插入排序结束 */ #include "stdio.h" #define MAX 11 void main() { int a[MAX]={6,3,8,1,7,4,9,12,52,54,2}; int i;//控制循环趟数 以及 待排序元素的下标 int j;//控制有序数组的下标 int temp;//存放 待排序元素 temp数据类型 与数组类型一致 int k;//增量 k代表把元素分为几组 //希尔排序开始 for(k=MAX/2;k>=1;k=k/2) // 缩小增量排序 继续分组 继续进行直接插入排序 { //直接插入排序开始 for(i=k;i<MAX;i++) { temp=a[i];//待排序元素 if(temp<a[i-k]) { for(j=i-k;a[j]>temp&&j>=0;j=j-k)//i-k有序数组最后一个元素的下标 { a[j+k]=a[j]; } //当我们结束第二层for循环时候,结束时j=j-k a[j+k]=temp; } } //直接插入排序结束 } //希尔排序结束 printf("希尔排序结果: "); for(i=0;i<MAX;i++) { printf("%d ",a[i]); } }
代码直接插入法
/* Note:Your choice is C IDE */
#include "stdio.h"
#define N 8
void main()
{
int i,j,tem,a[N]={ 13,6,3,31,9,27,5,11};
for(i=1;i<N;i++){
tem=a[i];
if(tem<a[i-1]){
j=i-1;
while(tem<a[j]&&j>=0){
a[j+1]=a[j];
j--;
}
a[j+1]=tem;
}
}
for(i=0;i<N;i++){
printf("%d ",a[i]);
}
}