原题链接:相似的字串
题意:
(给定长为n的字符串s,要取出k个位置不相交的字符串,取这k个串中任意两个最长公共前缀最小的最为 x)
(对所有符合条件的k,求出情况最大的x)
样例:
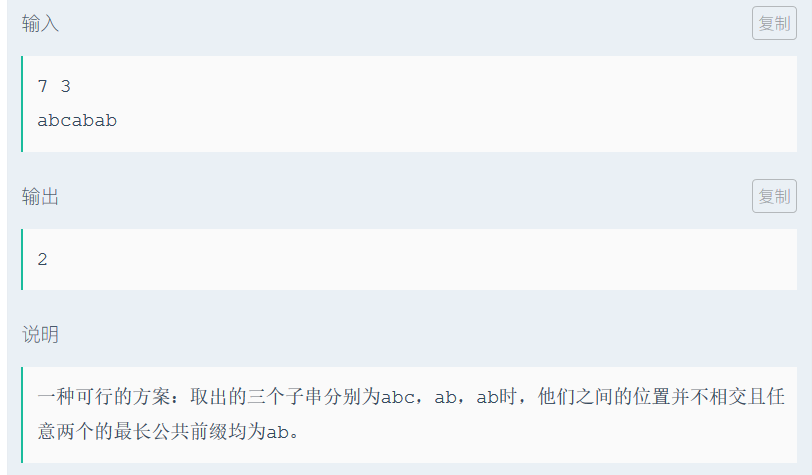
思路:
求相同前缀匹配方式可以通过 进制hash 来处理,同时对于符合条件的长度,使用二分来优化时间复杂度。
实际上这里就运用了 字串hash值的方式,我们设定数组 (f[i]) 表示已(i)为右端点的字串,然后每次截取从二分得到的(x)长度,记录相同子串的个数,如果个数大于给定的条件(k),则更新长度答案。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0); cin.tie(0);
typedef unsigned long long ull;
using namespace std;
const int maxn = 2e5+5;
ull base = 131;
ull p[maxn],h[maxn];
int f[maxn];//代表以下标为右端点
char s[maxn];
int n,k;
unordered_map<ull,int> Last;
ull get_hash(int l,int r){
return h[l] - h[r+1]*p[r-l+1];
}
bool check(int x){
f[0] = 0;
int res = 0;
//枚举所有起点
for(int i=1;i<=n-x+1;i++){
if( i-x > 0)
Last[get_hash(i-x,i-1)] = i-x;//记录最近出现的hash值位置(i-x为起点
f[i] = f[Last[get_hash(i,i+x-1)]] + 1;//当前位置等于之前相同hash值的个数+1
res = max(res,f[i]);
}
for(int i=1;i<=n-x+1;i++)
Last[get_hash(i,i+x-1)] = 0;//清空
//Last.clear();
return res >= k;//个数是否超过k
}
int main(){
IOS
cin>>n>>k;
cin>>(s+1);
p[0] = 1;
h[n+1] = 0;
for(int i=1;i<=n;i++){
h[n-i+1] = h[n-i+2]*base + s[n-i+1] - 'a';
p[i] = p[i-1]*base;
}
int ans = 0;
int l=1,r=n;//二分最大长度
while(l<=r){
int mid = (l+r)>>1;
if(check(mid)){
ans = max(ans,mid);
l = mid + 1;
}else{
r = mid - 1;
}
}
cout<<ans<<endl;
return 0;
}