https://www.luogu.org/problemnew/show/1251
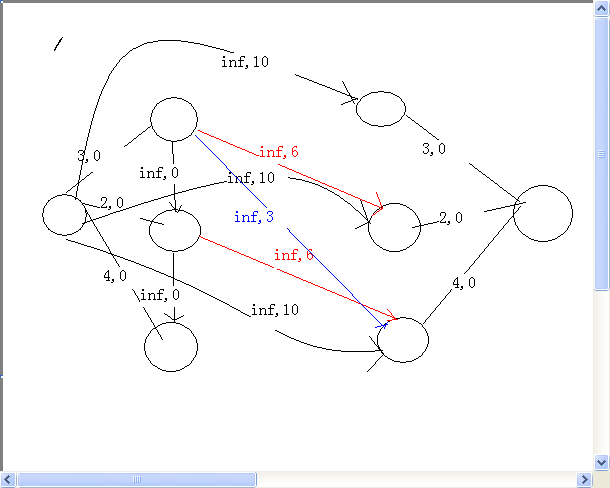
样例的构图:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 4005 #define M 12001 const int inf=1e17; typedef long long LL; int tot=1; int front[N],to[M<<1],nxt[M<<1],from[M<<1]; int cap[M<<1]; int val[M<<1]; int src,decc; LL cost; bool vis[N]; LL dis[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v,int w,int f) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; from[tot]=u; cap[tot]=w; val[tot]=f; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; from[tot]=v; cap[tot]=0; val[tot]=-f; } int augment(int now,int flow) { vis[now]=true; if(now==decc) { cost-=dis[src]*flow; return flow; } int delta; for(int i=front[now];i;i=nxt[i]) { if(cap[i] && !vis[to[i]] && dis[to[i]]==dis[now]+val[i]) { delta=augment(to[i],min(flow,cap[i])); if(delta) { cap[i]-=delta; cap[i^1]+=delta; return delta; } } } return 0; } bool retreat() { if(vis[decc]) return true; LL mi=inf; for(int i=2;i<=tot;++i) if(cap[i] && vis[from[i]] && !vis[to[i]]) mi=min(mi,dis[from[i]]+val[i]-dis[to[i]]); if(mi==inf) return false; for(int i=src;i<=decc;++i) if(vis[i]) dis[i]-=mi; return true; } void zkw() { do { memset(vis,false,sizeof(vis)); augment(src,inf); }while(retreat()); cout<<cost; } int main() { freopen("napkin.in","r",stdin); freopen("napkin.out","w",stdout); int n,x; read(n); decc=n*2+1; for(int i=1;i<=n;++i) { read(x); add(src,i,x,0); add(i+n,decc,x,0); } for(int i=1;i<n;++i) add(i,i+1,inf,0); int p; read(p); for(int i=1;i<=n;++i) add(src,i+n,inf,p); int a,b; read(a); read(b); for(int i=1;i+a<=n;++i) add(i,i+a+n,inf,b); read(a); read(b); for(int i=1;i+a<=n;++i) add(i,i+a+n,inf,b); zkw(); }
题目描述
一个餐厅在相继的N天里,第i天需要Ri块餐巾(i=l,2,…,N)。餐厅可以从三种途径获得餐巾。
(1)购买新的餐巾,每块需p分;
(2)把用过的餐巾送到快洗部,洗一块需m天,费用需f分(f<p)。如m=l时,第一天送到快洗部的餐巾第二天就可以使用了,送慢洗的情况也如此。
(3)把餐巾送到慢洗部,洗一块需n天(n>m),费用需s分(s<f)。
在每天结束时,餐厅必须决定多少块用过的餐巾送到快洗部,多少块送慢洗部。在每天开始时,餐厅必须决定是否购买新餐巾及多少,使洗好的和新购的餐巾之和满足当天的需求量Ri,并使N天总的费用最小
输入输出格式
输入格式:
输入文件共3行,第1行为总天数;第2行为每天所需的餐巾块数;第3行为每块餐巾的新购费用p,快洗所需天数m,快洗所需费用f,慢洗所需天数n,慢洗所需费用s。
输出格式:
输出文件共1行为最小的费用。
输入输出样例
说明
N<=2000
ri<=10000000
p,f,s<=10000