三维形体的表面积
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
示例 1:
输入:[[2]]
输出:10
示例 2:
输入:[[1,2],[3,4]]
输出:34
示例 3:
输入:[[1,0],[0,2]]
输出:16
示例 4:
输入:[[1,1,1],[1,0,1],[1,1,1]]
输出:32
示例 5:
输入:[[2,2,2],[2,1,2],[2,2,2]]
输出:46
示例图
示例 1:
输入:[[2]]
输出:10
这个图长这样
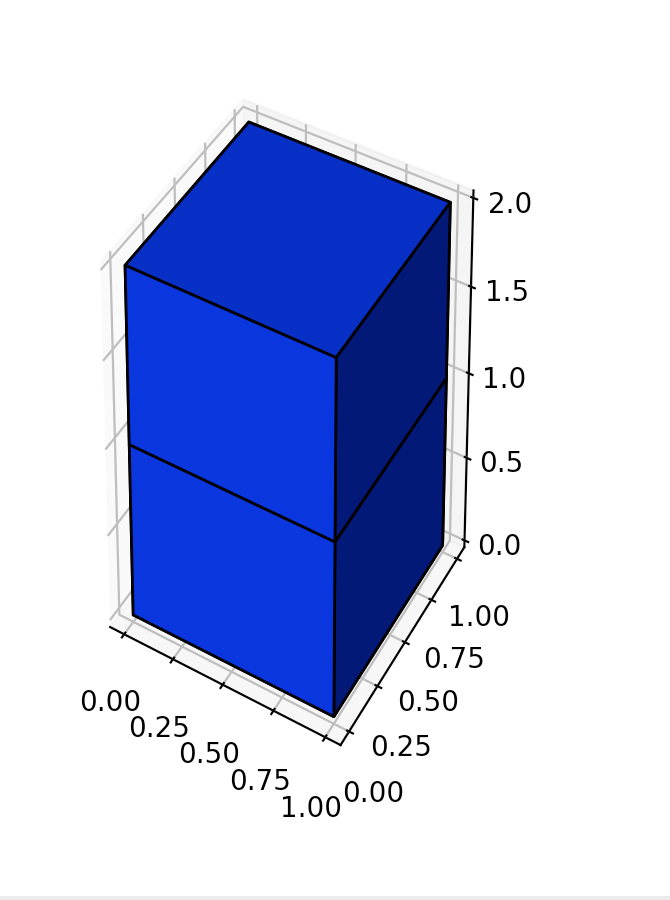
2 个立方体分别贡献了 5 个单位的表面积。
示例 2:
输入:[[1,2],[3,4]]
输出:34
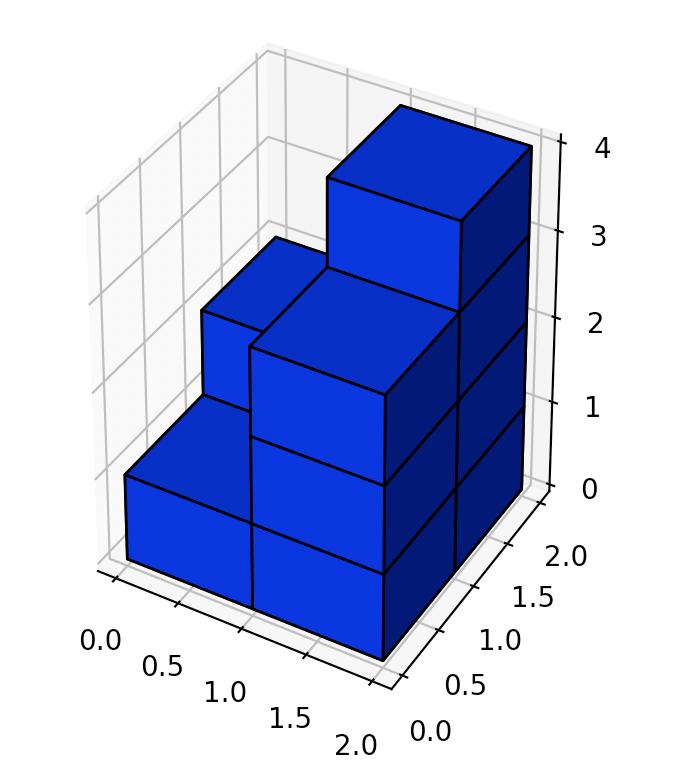
示例 3:
输入:[[1,0],[0,2]]
输出:16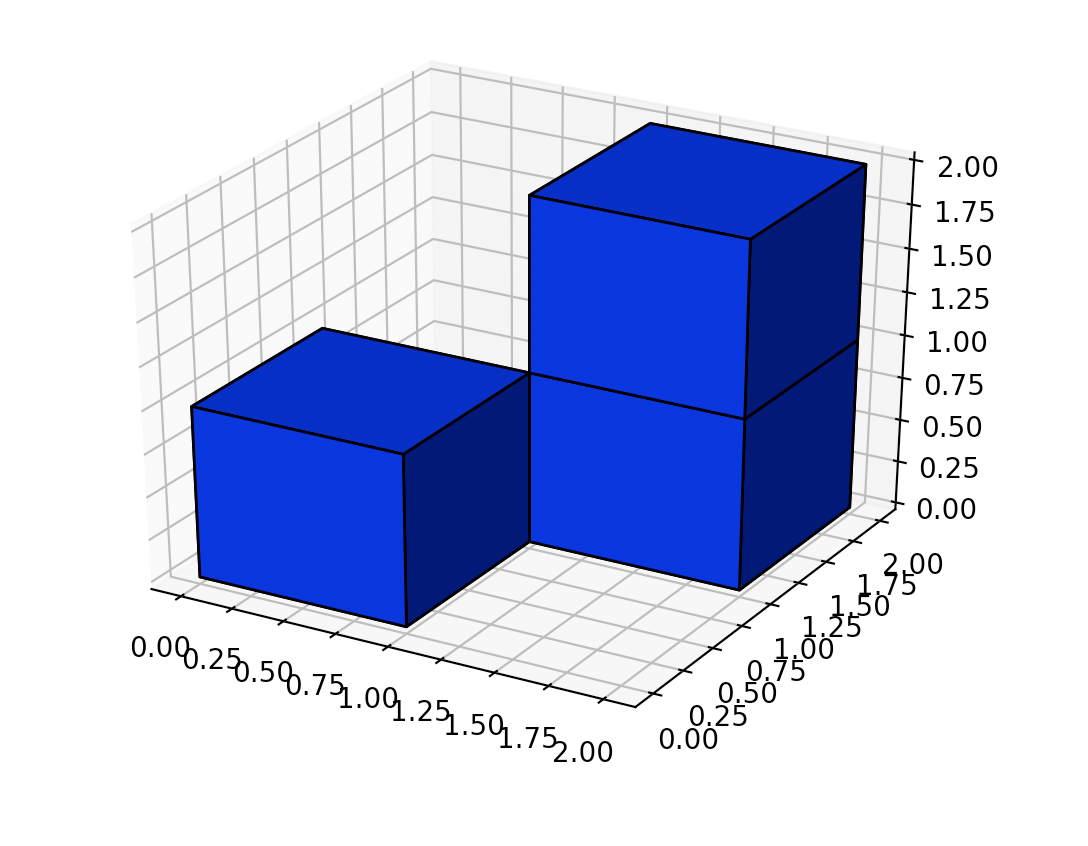
示例 4:
输入:[[1,1,1],[1,0,1],[1,1,1]]
输出:32
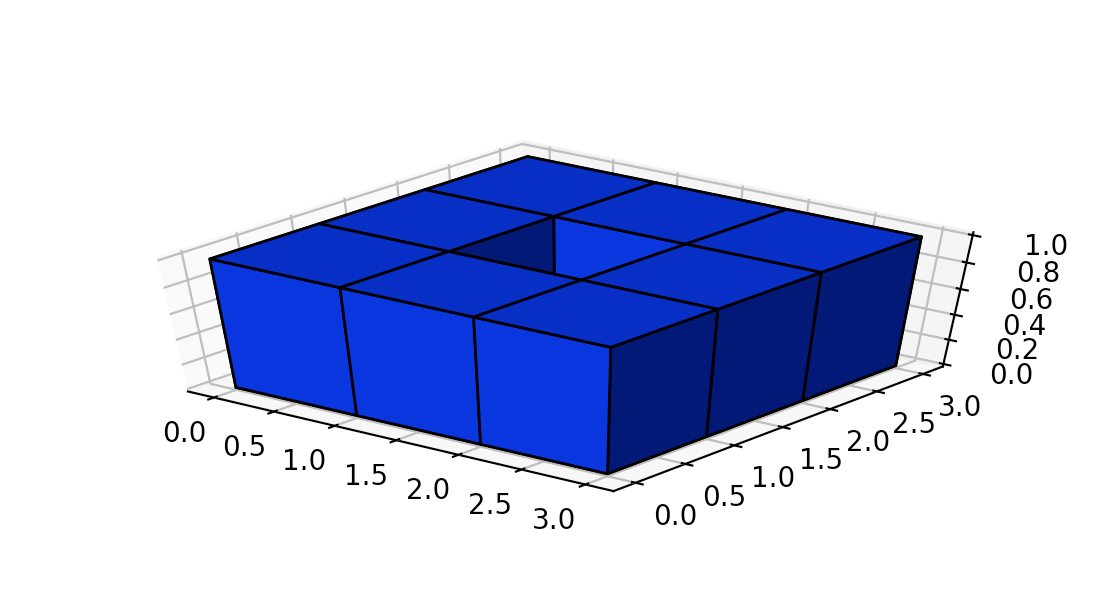
中间是空心的!但是空心处那几个表面积也是要算的!
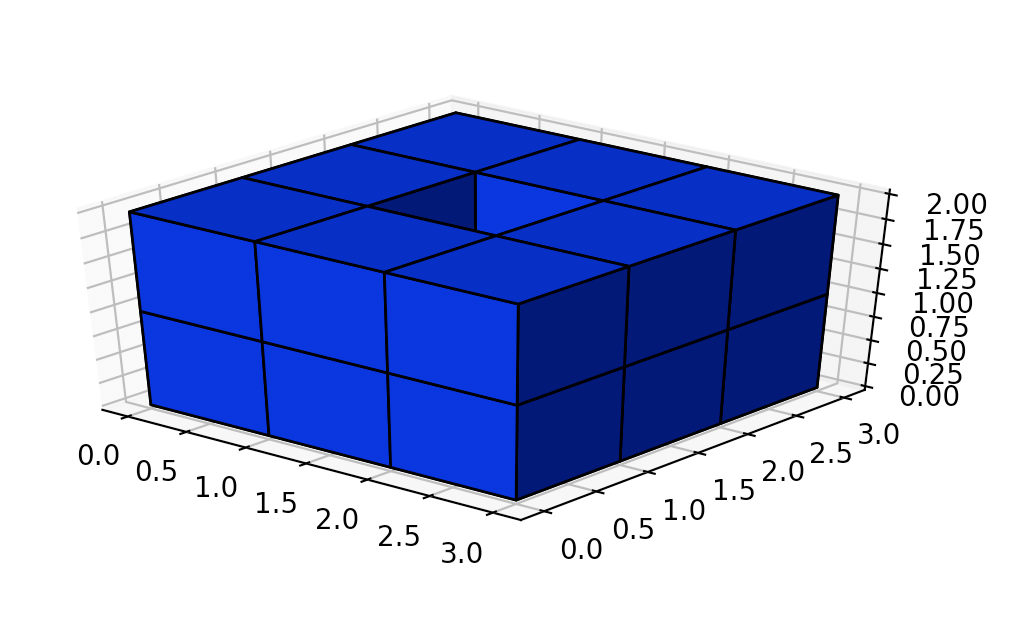
示例 5:
输入:[[2,2,2],[2,1,2],[2,2,2]]
输出:46
做法:
首先,一个柱体一个柱体的看,每个柱体是由:2 个底面(上表面/下表面)+ 所有的正方体都贡献了 4 个侧表面积。
然后,把柱体贴合在一起之后,我们需要把贴合的表面积给减掉,两个柱体贴合的表面积就是 两个柱体高的最小值*2。