在经过 \(n\) 个小时的奋斗后,LsWn 终于 AC 了这个毒瘤题。
我们先看一个正确可以流通的图 (加上了黑白相间染色,然后黄色方块代表这个格子的上方,红色代表下方,紫色是左,灰色是右)(最后一行的上下画反了……凑活凑活)。

黑白染色网络流一贯的套路,将黑点流向白点,源点流向黑点,白点流向汇点,然后根据拆点一贯的套路,内部连边。(指一个点拆成五个点,中间和上下左右)
显然,合理的方案就是所有的黑点和白点互相匹配,即有完备匹配,也就是满流,没有一滴水漏出来。从黑点流出的点都有去处。
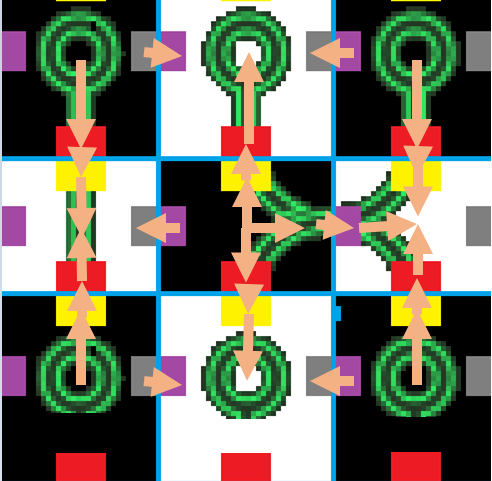
这是一个合法方案。那么如果出了点小差错,需要旋转呢?

这就很谔谔,右下角没法连通。但是我们可以旋转。我们观察到,左旋一次,相当于把右插头换成左插头。于是连费用为 \(1\) 的边。
右旋一次,相当于把下插头换成上插头,于是连边。。旋转两次,走两次旋转一次,故不连边。
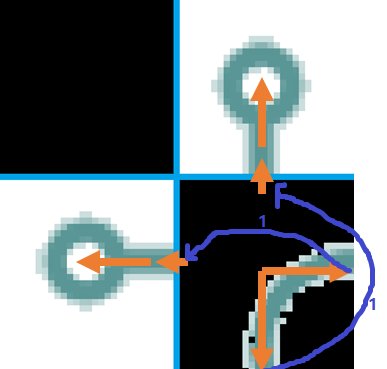
现在讨论连边情况:
- 类似于 ┌
上面已经讲过,不再陈述。 - 类似于 Q
如果左/右翻转,那么就等于插头向左/右换。翻转两次就是上下换,左右换。换两次的连边的费用是 \(2\)。 - 类似于丨
不处理,因为不能转。 - 类似于 T
和 ┌ 比较相似。不过需要连上下边。
5 类似于 十
不处理,因为转了也没用。
然后总体 \(15\) 种情况还需一一分析……这就很毒瘤。这就放在代码中了。
一些细节:
- 不要重复建边!不要重复建边!不要重复建边!(否则你算出来的答案会小于标准答案)
- 毒瘤建边题的网络流真的不能码错!真的不能!
- hsh 函数一定要注意!
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e6+9,inf=0x3f3f3f3f3f3f3f3f;
int n,m,a[2009][2009],debugger;
struct edge{int to,nxt,c,w;}e[N*2]; int hd[N],tot=1;
void add(int u,int v,int c,int w){e[++tot]=(edge){v,hd[u],c,w};hd[u]=tot;}
void addh(int u,int v,int c,int w){
//cout<<u<<" "<<v<<" "<<c<<" "<<w<<endl;
debugger+=w;
add(u,v,c,w),add(v,u,0,-w);
}
void addr(int u,int v,int c,int w){addh(v,u,c,w);}
int s,t,flow,cost,tmp,ans;
int d[N]; bool in[N];
bool spfa(){
queue<int>q; q.push(s); memset(d,0x3f,sizeof(d)); d[s]=0;
while(!q.empty()){
int u=q.front(); q.pop(); in[u]=0;
for(int i=hd[u],v;i;i=e[i].nxt)
if(e[i].c&&d[v=e[i].to]>d[u]+e[i].w){
d[v]=d[u]+e[i].w;
if(!in[v]) q.push(v),in[v]=1;
}
}
return d[t]<inf;
}
int dinic(int u,int flow){
int rest=flow; if(u==t) return flow; in[u]=1;
for(int i=hd[u],v;i&&rest;i=e[i].nxt)
if(!in[v=e[i].to]&&e[i].c&&d[v]==d[u]+e[i].w){
int used=dinic(v,min(e[i].c,rest));
if(!used) d[v]=-1;
rest-=used; e[i].c-=used,e[i^1].c+=used,cost+=used*e[i].w;
}
in[u]=0;
return flow-rest;
}
// 0:中 1:上 2:右 3:下 4:左
int hsh(int x,int y,int loc){return (x*m-m+y)+loc*m*n;}
bool ok(int x,int y){return x>0&&x<=n&&y>0&&y<=m;}
signed main(){
scanf("%lld%lld",&n,&m); s=n*m*5+1,t=n*m*5+2;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&a[i][j]);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
if((i+j)%2){ //黑格子
addh(s,hsh(i,j,0),inf,0);
if(ok(i-1,j))
addh(hsh(i,j,1),hsh(i-1,j,3),1,0);
if(ok(i,j+1))
addh(hsh(i,j,2),hsh(i,j+1,4),1,0);
if(ok(i+1,j))
addh(hsh(i,j,3),hsh(i+1,j,1),1,0);
if(ok(i,j-1))
addh(hsh(i,j,4),hsh(i,j-1,2),1,0);
for(int k=1;k<=4;k++)
if(a[i][j]&(1ll<<(k-1))){
addh(hsh(i,j,0),hsh(i,j,k),1,0);
ans++;
}
if(a[i][j]==15); //全
else if(a[i][j]==1){ //上
addh(hsh(i,j,1),hsh(i,j,2),1,1);
addh(hsh(i,j,1),hsh(i,j,4),1,1);
addh(hsh(i,j,1),hsh(i,j,3),1,2);
}
else if(a[i][j]==2){ //右
addh(hsh(i,j,2),hsh(i,j,1),1,1);
addh(hsh(i,j,2),hsh(i,j,3),1,1);
addh(hsh(i,j,2),hsh(i,j,4),1,2);
}
else if(a[i][j]==3){ //上右
addh(hsh(i,j,1),hsh(i,j,3),1,1);
addh(hsh(i,j,2),hsh(i,j,4),1,1);
}
else if(a[i][j]==4){ //下
addh(hsh(i,j,3),hsh(i,j,2),1,1);
addh(hsh(i,j,3),hsh(i,j,4),1,1);
addh(hsh(i,j,3),hsh(i,j,1),1,2);
}
else if(a[i][j]==5); //上下
else if(a[i][j]==6){ //右下
addh(hsh(i,j,3),hsh(i,j,1),1,1);
addh(hsh(i,j,2),hsh(i,j,4),1,1);
}
else if(a[i][j]==7){ //上右下
addh(hsh(i,j,1),hsh(i,j,4),1,1);
addh(hsh(i,j,3),hsh(i,j,4),1,1);
addh(hsh(i,j,2),hsh(i,j,4),1,2);
}
else if(a[i][j]==8){ //左
addh(hsh(i,j,4),hsh(i,j,1),1,1);
addh(hsh(i,j,4),hsh(i,j,3),1,1);
addh(hsh(i,j,4),hsh(i,j,2),1,2);
}
else if(a[i][j]==9){ //上左
addh(hsh(i,j,1),hsh(i,j,3),1,1);
addh(hsh(i,j,4),hsh(i,j,2),1,1);
}
else if(a[i][j]==10);//右左
else if(a[i][j]==11){//上右左
addh(hsh(i,j,2),hsh(i,j,3),1,1);
addh(hsh(i,j,4),hsh(i,j,3),1,1);
addh(hsh(i,j,1),hsh(i,j,3),1,2);
}
else if(a[i][j]==12){//下左
addh(hsh(i,j,3),hsh(i,j,1),1,1);
addh(hsh(i,j,4),hsh(i,j,2),1,1);
}
else if(a[i][j]==13){//上下左
addh(hsh(i,j,1),hsh(i,j,2),1,1);
addh(hsh(i,j,3),hsh(i,j,2),1,1);
addh(hsh(i,j,4),hsh(i,j,2),1,2);
}
else if(a[i][j]==14){//右下左
addh(hsh(i,j,2),hsh(i,j,1),1,1);
addh(hsh(i,j,4),hsh(i,j,1),1,1);
addh(hsh(i,j,3),hsh(i,j,1),1,2);
}
}
else{
addh(hsh(i,j,0),t,inf,0);
for(int k=1;k<=4;k++)
if(a[i][j]&(1<<(k-1))){
addr(hsh(i,j,0),hsh(i,j,k),1,0);
ans++;
}
if(a[i][j]==15); //全
else if(a[i][j]==1){ //上
addr(hsh(i,j,1),hsh(i,j,2),1,1);
addr(hsh(i,j,1),hsh(i,j,4),1,1);
addr(hsh(i,j,1),hsh(i,j,3),1,2);
}
else if(a[i][j]==2){ //右
addr(hsh(i,j,2),hsh(i,j,1),1,1);
addr(hsh(i,j,2),hsh(i,j,3),1,1);
addr(hsh(i,j,2),hsh(i,j,4),1,2);
}
else if(a[i][j]==3){ //上右
addr(hsh(i,j,1),hsh(i,j,3),1,1);
addr(hsh(i,j,2),hsh(i,j,4),1,1);
}
else if(a[i][j]==4){ //下
addr(hsh(i,j,3),hsh(i,j,2),1,1);
addr(hsh(i,j,3),hsh(i,j,4),1,1);
addr(hsh(i,j,3),hsh(i,j,1),1,2);
}
else if(a[i][j]==5); //上下
else if(a[i][j]==6){ //右下
addr(hsh(i,j,3),hsh(i,j,1),1,1);
addr(hsh(i,j,2),hsh(i,j,4),1,1);
}
else if(a[i][j]==7){ //上右下
addr(hsh(i,j,1),hsh(i,j,4),1,1);
addr(hsh(i,j,3),hsh(i,j,4),1,1);
addr(hsh(i,j,2),hsh(i,j,4),1,2);
}
else if(a[i][j]==8){ //左
addr(hsh(i,j,4),hsh(i,j,1),1,1);
addr(hsh(i,j,4),hsh(i,j,3),1,1);
addr(hsh(i,j,4),hsh(i,j,2),1,2);
}
else if(a[i][j]==9){ //上左
addr(hsh(i,j,1),hsh(i,j,3),1,1);
addr(hsh(i,j,4),hsh(i,j,2),1,1);
}
else if(a[i][j]==10);//右左
else if(a[i][j]==11){//上右左
addr(hsh(i,j,2),hsh(i,j,3),1,1);
addr(hsh(i,j,4),hsh(i,j,3),1,1);
addr(hsh(i,j,1),hsh(i,j,3),1,2);
}
else if(a[i][j]==12){//下左
addr(hsh(i,j,3),hsh(i,j,1),1,1);
addr(hsh(i,j,4),hsh(i,j,2),1,1);
}
else if(a[i][j]==13){//上下左
addr(hsh(i,j,1),hsh(i,j,2),1,1);
addr(hsh(i,j,3),hsh(i,j,2),1,1);
addr(hsh(i,j,4),hsh(i,j,2),1,2);
}
else if(a[i][j]==14){//右下左
addr(hsh(i,j,2),hsh(i,j,1),1,1);
addr(hsh(i,j,4),hsh(i,j,1),1,1);
addr(hsh(i,j,3),hsh(i,j,1),1,2);
}
}
}
while(spfa()) while(tmp=dinic(s,inf)) flow+=tmp;
if(flow*2==ans) printf("%lld\n",cost);
else puts("-1");
return 0;
}