一 Unsupervised Learning
把Unsupervised Learning分为两大类:
- 化繁为简:有很多种input,进行抽象化处理,只有input没有output
- 无中生有:随机给一个input,自动画一张图,只有output没有input

二 Clustering
有一大堆image ,把他们分为几大类,给他们贴上标签,将不同的image用相同的 cluster表示。 也面临一个问题,要有多少种cluster呢? 有两种clustering的方法:

2.1 K-means(K均值)
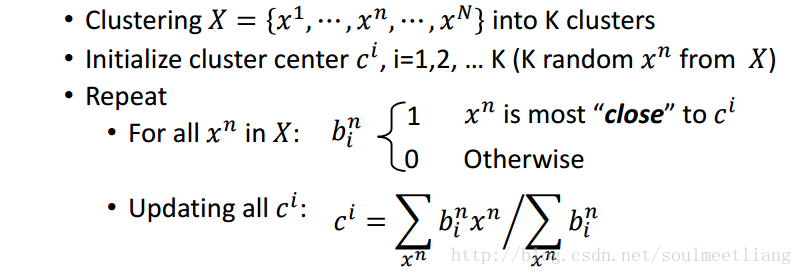
2.2 Hierarchical Agglomerative Clustering (HAC阶层式汇聚分群法)
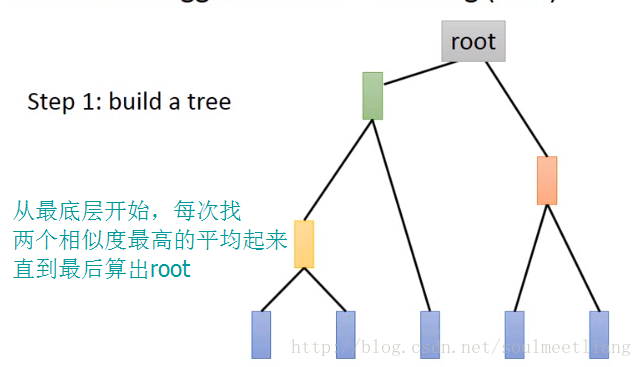
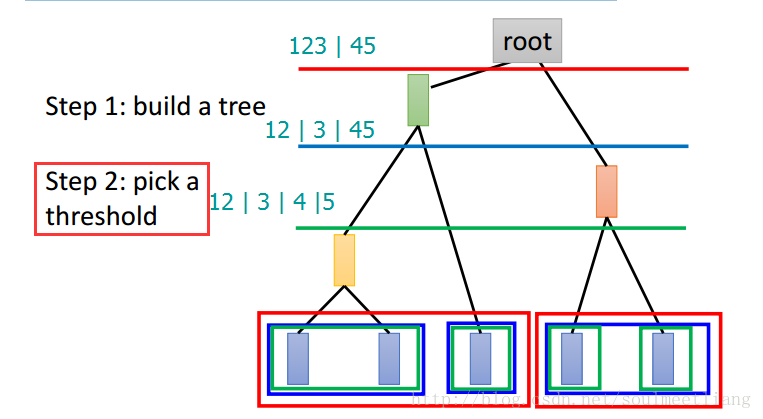
注:如果说K均值算法的问题是不好却确定分为几类,那么HAC的问题在于不知将分类门槛划在哪一层。
三 Distributed Representation(分布式表征)
光做clustering是很卡的,有的个体并不只属于一个大类,所以需要一个vector来表示在各个类中的概率。这样,从一个(高维)图片到一个各个属性概率(低维)就是一个Dimension Reduction。
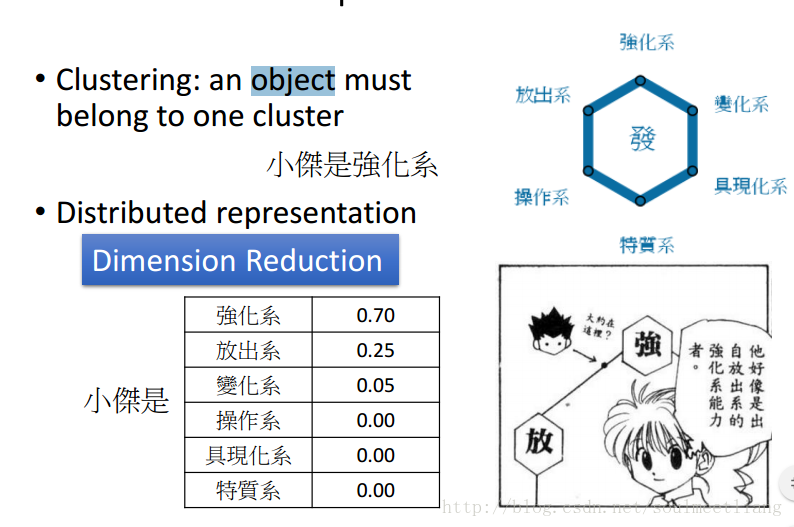
四 Dimension Reduction
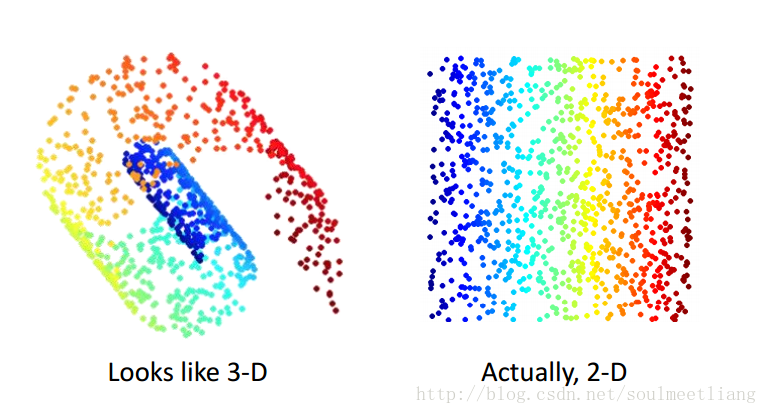
为什么说降维是很有用的呢? 有时候在3D很复杂的图像到2D就被简化了。
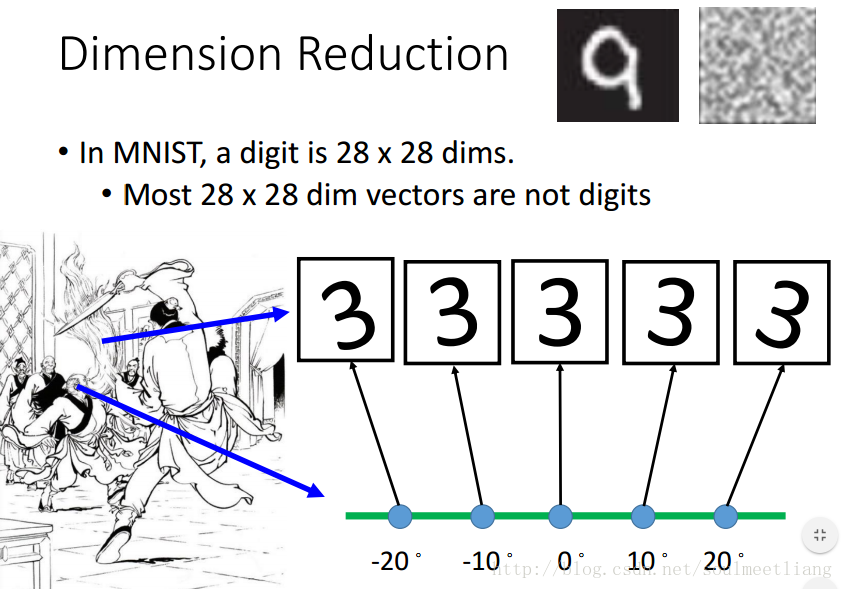
在MNIST训练集中,很多28*28维的向量转成一个image看起来根本不像数字,其中是digit的vector很少,所以或许我们可以用少于28*28维的向量来描述它。 比如下图一堆3,每一个都是28*28维的向量,但是,我们发现,它们仅仅是角度的不同,所以我们可以加上角度值进行降维,来简化表示。
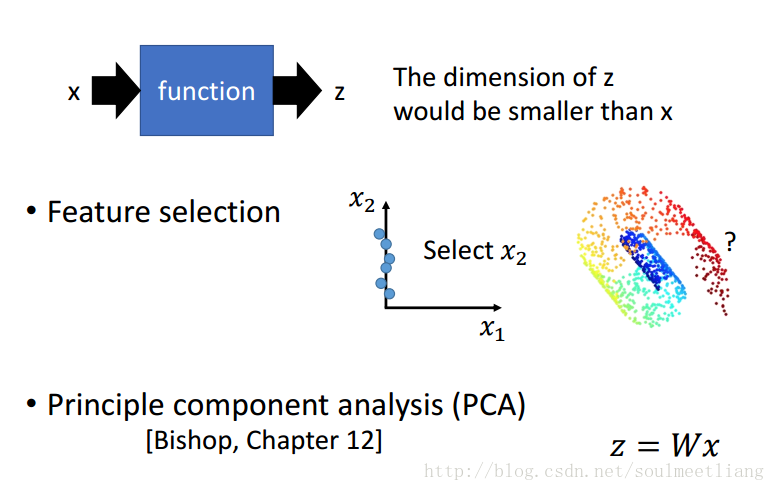
那我们应该怎样做Dimension Reduction呢? 就是要找一个function。有两个方法:
- Feature selection特征选择:比如在左图二维坐标系中,我们发现X1轴对样本点影响不大,那么就可以把它拿掉。
- PCA 主成分分析: 输出 z=Wx输入,找到这个向量W。
在现实中我们很难确定某个因素是否真的不起作用,所以下边重点介绍一个PCA
4.1 Principle Component Analysis (PCA) 主成分分析
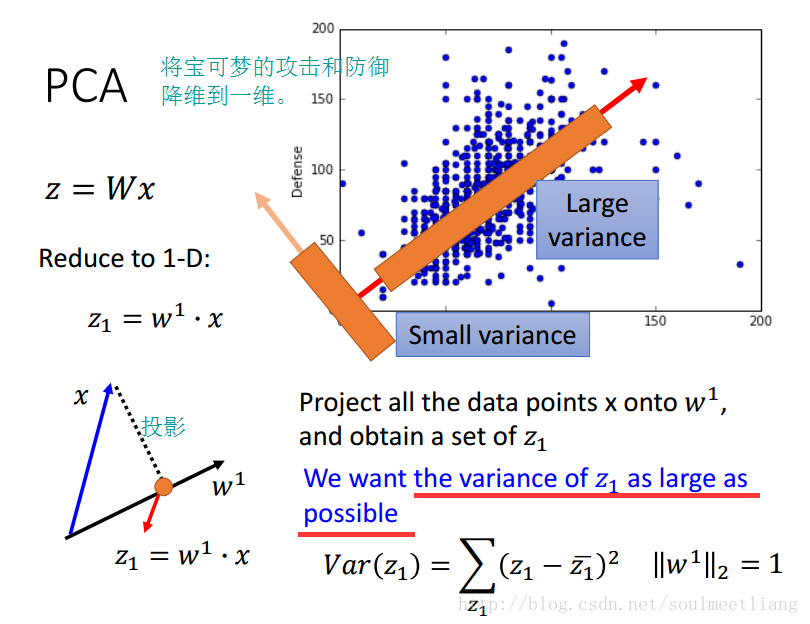
在一维的例子里,我们要找 z1 方差最大的情况,当维度升高到2维,找 z2 方差最大,为了避免与 z1 重复,所以规定 w1 与 w2 垂直。依次方法可进行高维计算。将所有w转置一下,组成一个高维向量,就是我们要找的W。
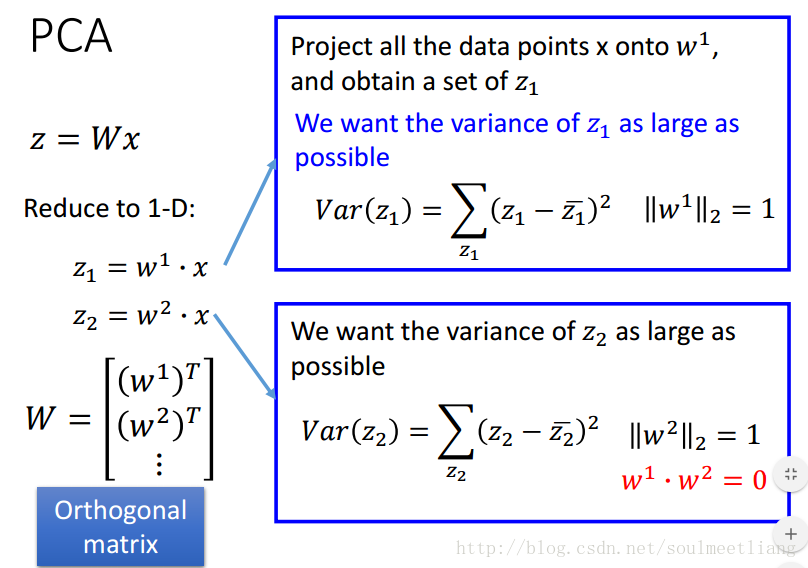
补充一些数学知识(为了求解w):



4.2 PCA - decorrelation

4.3 PCA – Another Point of View
每个手写识别,都是由基础组件构成的,把基础组件加起来,得到一个数字。 对7来说,C1C2C3C4C5分别为1�1�1
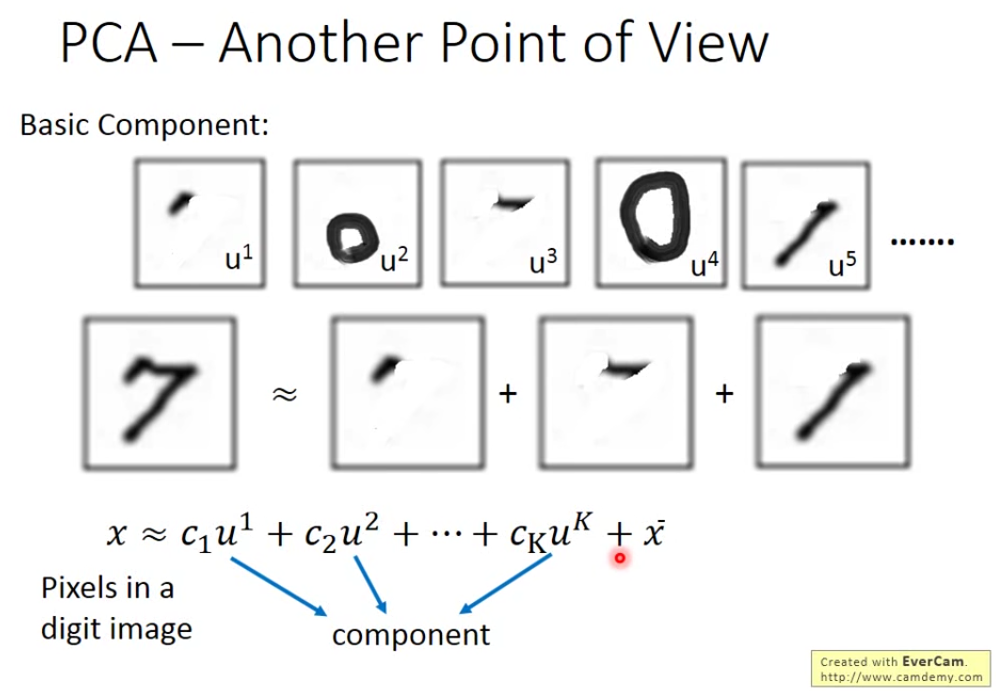
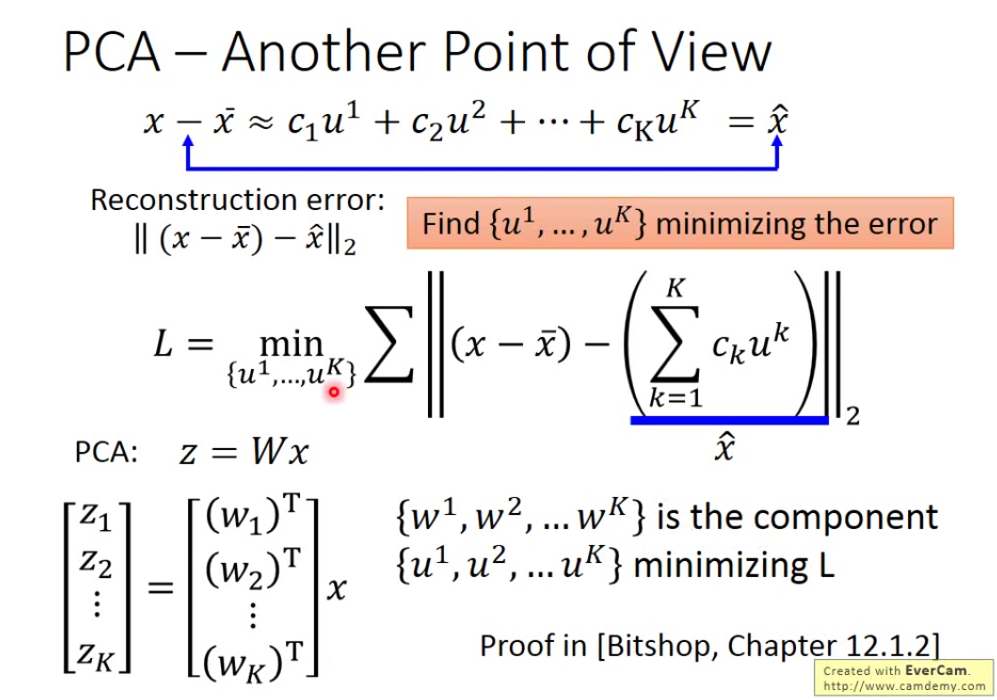
那我们如何找到 u1-uK这K个Vector呢? 我们要找K个vector使重构误差越小越好。
转化为Matrix。
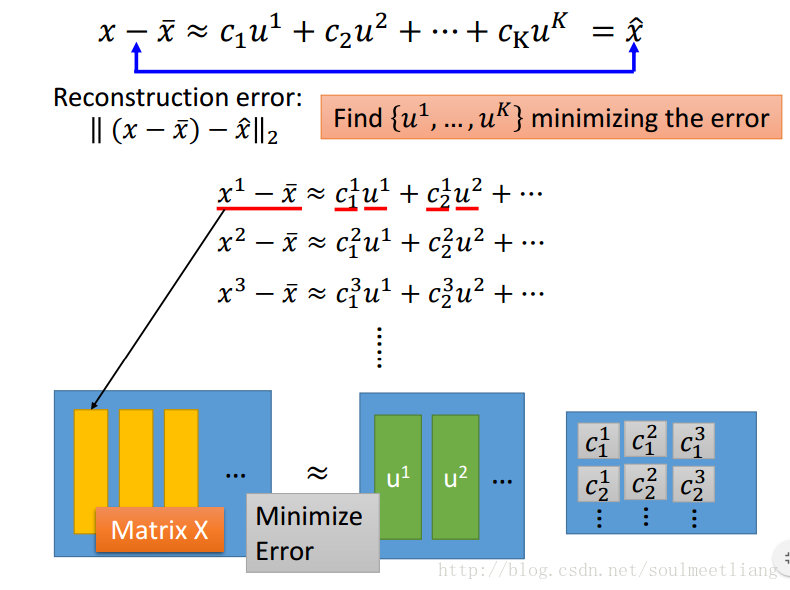
怎么解这个问题呢?SVD方法: matrix X 可以用SVD拆成 matrix U * matrix ∑ * matrix V。
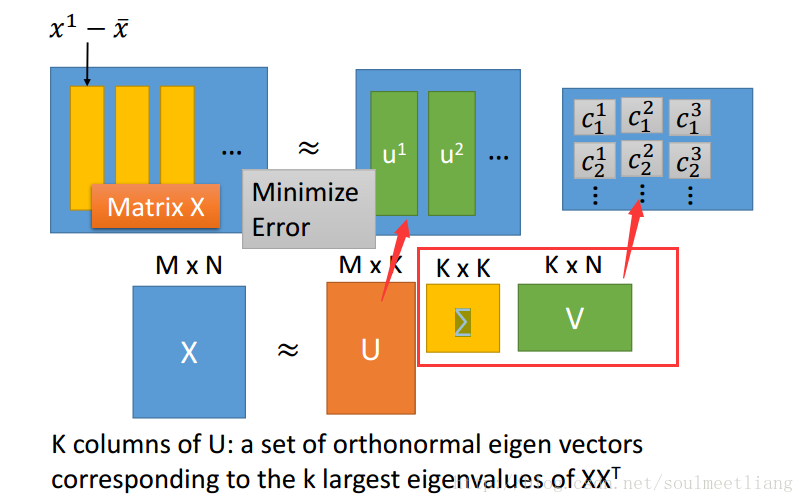
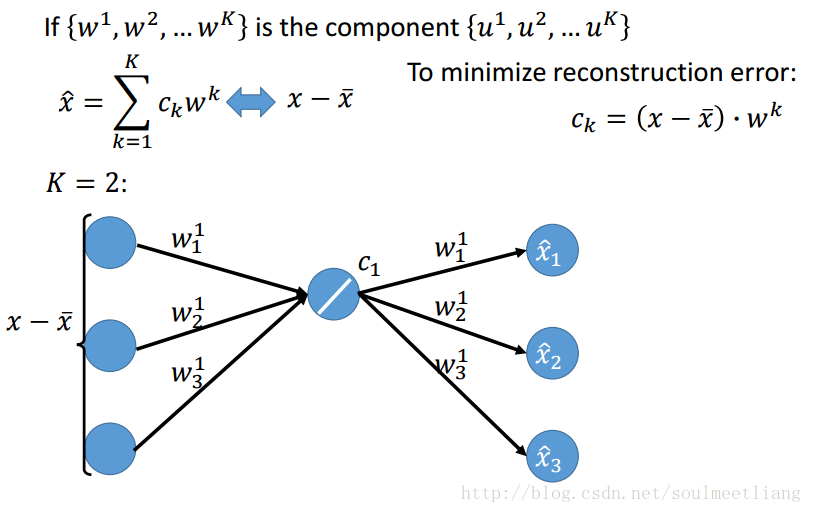
这样w已经通过SVD求出来了,Ck怎么求呢?
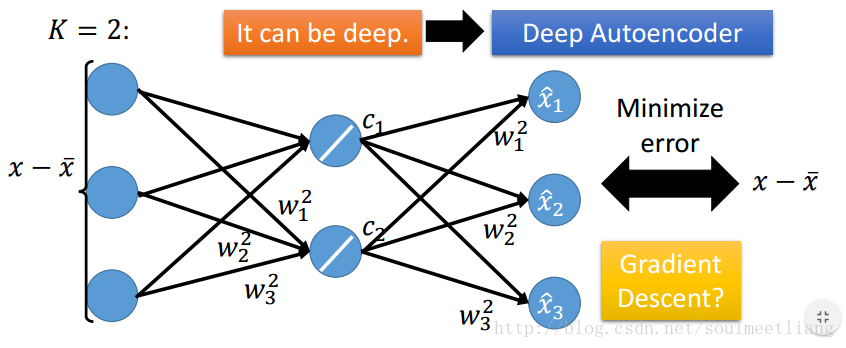
4.4 Weakness of PCA

参考:
http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/dim%20reduction%20%28v5%29.pdf
https://blog.csdn.net/soulmeetliang/article/details/73309360