栈的应用--迷宫问题

问题描述：给定一个迷宫，给定入口和出口，找到从入口到出口的一条路径(任何一条路径都可以)，迷宫为0表示可走，为1表示墙。用1将迷宫围起来避免边界问题。

实现思路：1.DFS搜索（递归）

2.采用栈的数据结构

下面分别用这两种方法来解决这个问题。

DFS搜索（即递归+回溯）

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include <unistd.h>
#define ROW 9
#define COL 9

int integer[ROW][COL]={     //表示迷宫
    {1,0,1,1,1,1,1,1,1},
    {1,0,1,1,1,0,0,0,1},
    {1,0,0,0,0,0,1,0,1},
    {1,0,1,1,1,0,1,0,1},
    {1,0,1,0,0,0,1,0,1},
    {1,0,1,1,1,0,1,0,1},
    {1,0,0,0,0,1,1,0,1},
    {1,0,1,1,1,1,1,0,0},
    {1,1,1,1,1,1,1,1,1}
};
/*int integer[ROW][COL]={
    {2,0,2,2,2,2,2,2,2,2},//1
    {2,0,0,2,0,0,0,2,0,2},//2
    {2,0,0,2,0,0,0,2,0,2},//3
    {2,0,0,0,0,2,2,0,0,2},//4
    {2,0,2,2,2,0,0,0,0,2},//5
    {2,0,0,0,2,0,0,0,0,2},//6
    {2,0,2,0,0,0,2,0,0,2},//7
    {2,0,2,2,2,0,2,2,0,2},//8
    {2,2,0,0,0,0,0,0,0,0},//9
    {2,2,2,2,2,2,2,2,2,2} //10
}; 大家可以用这个迷宫进行再次观察*/

int  print(int integer[ROW][COL],int x,int y);//打印该迷宫

int dir[4][2]={
{1,0},{-1,0},
{0,1},{0,-1},
}  ;     //方向数组,代表 4 个方向

int visted[120][120] ;    //  1  代表访问过  0 代表没有访问过

int check(int x,int y) //检查下一步是否越界和是否已经走过以及是否是墙
{
    if(x< 0 || y<0 || x>= ROW || y>= COL)  
        return 0;
    if(visted[x][y])
        return 0;
    if(integer[x][y] !=  0 )
        return 0;
    return 1;
}

int dfs(int x,int y)    //已经踏到了  x , y ，即x,y  可踏
{
    int xx,yy ,i ;
    usleep(100000);
    printf("33c");
    print(integer,x,y);
    if(x ==  7 && y == 8 )
        exit(0);
    for(i= 0;i< 4 ;i++)   // 4 个方向 
    {
        xx =  x + dir[i][0];
        yy =  y + dir[i][1];
        if(check(xx,yy))    //xx ,yy 可踏上去
        {
            visted[xx][yy]= 1;
            dfs(xx,yy) ;
            visted[xx][yy] = 0 ;  //回溯
        }
    }
    usleep(100000); //再次打印，显示回溯的效果
    printf("33c");
    print(integer,x,y);
    return 0;
}

int print(int integer[ROW][COL],int x,int y)
{
    int i,j;
    for(i=0;i<ROW ;i++)
    {
        for(j=0 ;j<COL ;j++)
        {
            if(visted[i][j])
               printf("33[41;32m  *  33[0m") ;
            else 
                printf("  %d  ",integer[i][j]);
        }
        printf("

");
    }
}
int main(void)
{
    int i,j ;
    memset(visted,0,sizeof(visted));
    visted[0][1]=1;      //从入口出发
    dfs(0,1) ; 
}

运行截图：

PS 1.这是一个动态演示的程序，可以清晰的看到移动的动作，所以运行有奇效

2. 回溯之后要再打印一次，才能有回溯的效果，并且必须有sleep 函数，否则会因为程序运行太快而导致看不到回溯的效果。

3. 如果对于DFS搜索还不太懂的–>点这里,文中提到的马踏棋盘我会在下一篇博客中提到。

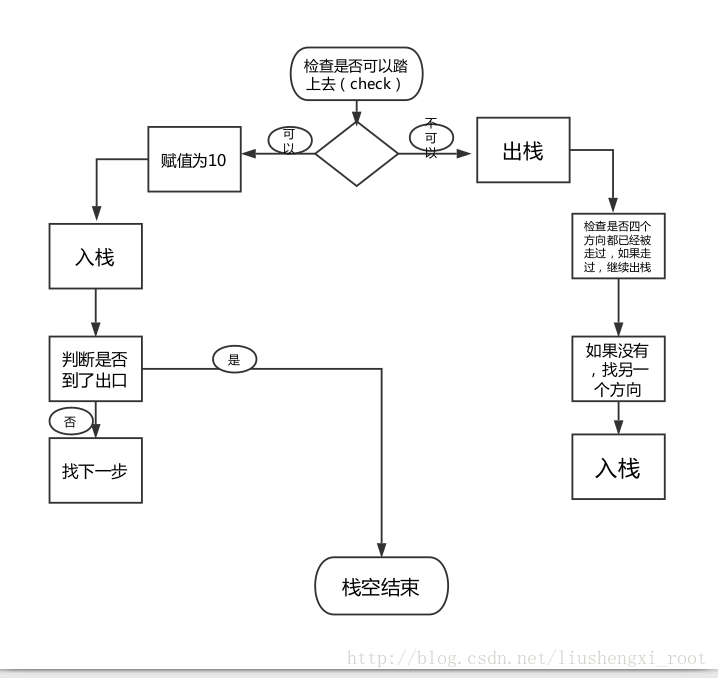
采用栈的数据结构

先来提出几个问题

1.为什么要用栈来实现？有什么好的地方？
2.di 有什么作用？为什么要它？
3.栈空与栈不空，有什么用？
4.大体思路是什么？

#include<stdio.h>
#include<stdlib.h>
#include <unistd.h>
#define  MAXSTACKSIZE  100  //栈的大小
#define      N          10     //二维迷宫大小
#define  Entrance_row   0  //入口
#define  Entrance_col   1 
#define  Exit_row   8   //出口
#define  Exit_col   9
typedef struct position{   //坐标   
    int x;
    int y;
}position ;
typedef struct SElement {
    position p;   
    int di;     //记录已经走了多少个方向
}SElement ; 
typedef struct Mystack{
    SElement  *top;
    SElement  *base;
    int stackSize ;
}Mystack ;

int Maze[N][N]={
    {2,0,2,2,2,2,2,2,2,2},//1
    {2,0,0,2,0,0,0,2,0,2},//2
    {2,0,0,2,0,0,0,2,2,2},//3
    {2,0,0,0,0,2,2,0,0,2},//4
    {2,0,2,2,2,0,2,0,2,2},//5
    {2,0,0,0,2,0,0,0,0,2},//6
    {2,0,2,0,0,0,2,0,0,2},//7
    {2,0,2,2,2,0,2,2,0,2},//8
    {2,2,0,0,0,0,0,0,0,0},//9
    {2,2,2,2,2,2,2,2,2,2} //10
};

int IsEmptyStack(Mystack *path);

int InitStack(Mystack *path)   // top ,base  ,size 
{
    path->top = path->base =(SElement *)malloc(sizeof(SElement)*MAXSTACKSIZE);
    if(path->top == NULL )
    {
        printf("Init  stack is failed !!! 
");
        return -1;
    }
    path->stackSize = MAXSTACKSIZE;
    return 0;
}

int pop(Mystack *path ,SElement *t)  //从path 中出一个元素给t 
{
    if(IsEmptyStack(path) == 1)
        return 0;
    *t = *(path->top-1);
    path->top-- ;
    return 1;
}

int push(Mystack *path ,SElement p) //入栈
{
    *(path->top) = p ;
    path->top++;
}

int IsEmptyStack(Mystack *path)
{
    if(path->top == path->base )   return 1;  //空栈返回 1  
    else return 0 ;
}
int print_MAZE(int Maze[N][N])  //打印迷宫
{
    int i,j;
    for(i= 0 ;i< N;i++)
    {
        for(j= 0 ;j< N ;j++)
        {
            if(Maze[i][j] == 10)    printf("33[31m  *  33[0m") ;
            else  printf("  %d  ",Maze[i][j]);
        }
        printf("

");
    }
}
int check(position now_try) //检查下一步是否越界和是否是墙 
{

    if(Maze[now_try.x][now_try.y]  !=  0)  //0  代表走的通
        return 0;
    if(now_try.x <  0 && now_try.x >=  N  )
        return 0;
    if(now_try.y <  0 && now_try.y >=  N  )
        return 0;
    return 1;
}

position   NextPosition(position  now_try ,int direction)  //获得下一个位置的坐标 x,y
{
    position next ;
    next.x= now_try.x;
    next.y  = now_try.y;
    switch(direction)
    {
        case 4:next.y+=1;break; //东
        case 3:next.x+=1;break; //南
        case 1:next.x-=1;break;//西
        case 2:next.y-=1;break;//北
    }
    return next ;
}
int main(void)
{
    print_MAZE(Maze) ;
    Mystack  path ;
    InitStack(&path);
    position  now_try ; //所尝试的位置
    now_try.x= Entrance_row;
    now_try.y= Entrance_col;
    do{
        if(check(now_try)) //进入if 语句就说明这个点能走，就把他赋值为10 ，入栈，找下一步，继续
        {
            Maze[now_try.x][now_try.y]  =10 ;
            SElement temp ;
            temp.p.x= now_try.x;
            temp.p.y= now_try.y;
            push(&path,temp);

            if(now_try.x == Exit_row && now_try.y == Exit_col )
                break;
            now_try  = NextPosition(now_try,1);  //先向一个方向进行探索
            printf("33c"); // 动态演示所走的路的语句
            print_MAZE(Maze);
            usleep(800000);
        }
        else     //这个点为 2 ,不能走，那么就取出它的上一个（即栈顶元素），寻找其他方向
        {
            if(IsEmptyStack(&path) !=  1)  //栈不空
            {
                SElement t ;
                pop(&path,&t);    //要在被调函数中改变t
                while(t.di == 4 && IsEmptyStack(&path) !=  1){   //检查是否四个方向都已经被走过
                    Maze[t.p.x][t.p.y] = 9 ;   //9 代表已经被探索过的路
                    pop(&path,&t);
                }
                if(t.di < 4) //如果四个方向没有走够，就换一个方向走
                {
                    now_try = NextPosition(t.p,t.di+1);
                    t.di++;
                    push(&path,t);
                }
            }
        }
    }while( IsEmptyStack(&path) ==  0  );  //0 就是有元素
    printf("33c");
    print_MAZE(Maze);
    return 0;
}

运行截图：

问题解答：

1.首先我们都知道栈有先进后出的特点，那么我们的迷宫是否需要这种特点呐。如果走的通，那么就走，如果走不通，那是不是要回到前一步，找另外一个方向走。那么前一步怎么存储？是不是符合一个先存后取的顺序！OK ！这不正好与我们的栈的特点重合吗。

2.di 的作用有两个。一是表示方向，二是表示走了几个方向了。是不是感觉很拗口。那么我来简单解释一下。用1，2，3，4来表示东南西北，如果di==3,那么就说明北面还没有走，如果di == 4,那么就说明四个方向都已经走过了。

3.栈空与栈不空，有什么用？假如我们将迷宫改成了这样，那么会发生什么？

int Maze[N][N]={
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,0,2,2,2,2,2,2,2,2},
    {2,2,2,2,2,2,2,2,2,2},
    {2,2,2,2,2,2,2,2,2,2} 
};

是不是会依次入栈，然后依次出栈，出栈之后是不是会栈空，如果不判断栈空的话是不是会陷入一种死循环的状态呐。

4.核心代码：

    now_try.x= Entrance_row;
    now_try.y= Entrance_col;
    do{
        if(check(now_try)) //进入if 语句就说明这个点能走，就把他赋值为10 ，入栈，找下一步，继续
        {
            Maze[now_try.x][now_try.y]  =10 ;
            SElement temp ;
            temp.p.x= now_try.x;
            temp.p.y= now_try.y;
            push(&path,temp);

            if(now_try.x == Exit_row && now_try.y == Exit_col )
                break;
            now_try  = NextPosition(now_try,1);  //先向一个方向进行探索
            printf("33c"); // 动态演示所走的路的语句
            print_MAZE(Maze);
            usleep(800000);
        }
        else     //这个点为 2 ,不能走，那么就取出它的上一个（即栈顶元素），寻找其他方向
        {
            if(IsEmptyStack(&path) !=  1)  //栈不空
            {
                SElement t ;
                pop(&path,&t);    //要在被调函数中改变t
                while(t.di == 4 && IsEmptyStack(&path) !=  1){   //检查是否四个方向都已经被走过
                    Maze[t.p.x][t.p.y] = 9 ;   //9 代表已经被探索过的路
                    pop(&path,&t);
                }
                if(t.di < 4) //如果四个方向没有走够，就换一个方向走
                {
                    now_try = NextPosition(t.p,t.di+1);
                    t.di++;
                    push(&path,t);
                }
            }
        }
    }while( IsEmptyStack(&path) ==  0  );  //0 就是有元素

大体思路：

参考资料：参考资料