• 浙大《数据结构》第四章：树(中)

    注：本文使用的网课资源为中国大学MOOC

    https://www.icourse163.org/course/ZJU-93001

    目录



    二叉搜索树

    定义

    二叉搜索树（BST, binary search tree），也称为二叉排序树或二叉查找树。

    二叉搜索树：可以为空，若不为空，则满足以下性质：

    1. 非空左子树的所有键值小于其根结点的键值；
    2. 非空右子树的所有键值大于其根结点的键值；
    3. 左右子树都是二叉搜索树。

    二叉搜索树的基本操作：

    BinTree Find( ElementType X, BinTree BST ); // 从BST中查找元素X，并返回其所在结点的地址
BinTree FindMin( BinTree BST ); // 从BST中查找并返回最小元素所在结点的地址
BinTree FindMax( BinTree BST ); // 从BST中查找并返回最大元素所在结点的地址
BinTree Insert( ElementType X, BinTree BST ); // 在BST中插入元素x，并使之仍保持为BST
BinTree Delete( ElementType X, BinTree BST ); // 在BST中删除元素x，并使之仍保持为BST

    BST的查找操作Find

    思路：

    1. 查找从根节点开始，如果树为空，返回NULL;
    2. 若BST非空，则根节点关键字和X进行比较，并进行不同的处理：
      • 若x小于根节点键值，则在左子树中继续搜索；
      • 若x大于根节点的键值，则在右子树中继续搜索；
      • 若两者比较结果是相等，搜索完成，返回指向此结点的指针
    BinTree Find( ElementType X, BinTree BST )
{
    if ( !BST )
        return NULL;
    if ( X > BST->Data )
        return Find( X, BST->Right ); // 在右子树继续查找
    else if ( X < BST->Data )
        return Find( X, BST->Left ); // 在左子树中继续查找
    else
        return BST; // 查找成功，返回结点的找到结点的地址
}

/* 迭代形式的Find函数 */
BinTree Find( ElementType X, BinTree BST )
{
    while ( BST )
    {
        if ( X > BST->Data )
            BST = BST->Right; // 向右子树移动，继续查找
        else if ( X < BST->Data )
            BST = BST->Left; // 向左子树中移动，继续查找
        else
            return BST; // 查找成功，返回结点的地址
    }
    return NULL; // 查找失败
}

    查找最大和最小元素

    • 最大元素一定是在树的最右分支的端结点上
    • 最小元素一定是在树的最左分支的端结点上
    • 若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小元素一定在叶结点上
    /* 递归形式的查找最小元素函数 */
BinTree FindMin( BinTree BST )
{
    if ( !BST )
        return NULL; // 空的二叉搜索树，返回NULL
    else if ( !BST->Left )
        return BST; // 找到最左叶结点并返回
    else
        return FindMin( BST->Left ); // 在左子树中继续查找
}

/* 迭代形式的查找最大元素函数 */
BinTree FindMax( BinTree BST )
{
    if ( BST )
    {
        while ( BST->Right)
            BST = BST->Right; // 沿右分支继续查找，知道最右叶结点
    }
    return BST; 
}

    BST的插入操作

    BinTree Insert( ElementType X, BinTree BST )
{
    if ( !BST )
    {
        // 若原树为空，生成并返回一个结点的二叉搜索树
        BST = (BinTree)malloc( sizeof(struct TreeNode) );
        BST->Data = X;
        BST->Left = BST-Right = NULL;
    }
    else // 开始找要插入的元素
    {
        if ( X < BST->Data )
            BST->Left = Insert( X, BST->Left ); // 递归插入左子树
        else if ( X > BST->Data )
            BST->Right = Insert( X, BST->Right); //递归插入右子树
    }
    return BST;

    BST的删除操作

    思路：

    考虑三种情况：

    1. 要删除的是叶结点：直接删除，并修改其父结点指针，置为NULL;
    2. 要删除的结点只有一个孩子结点：将其父结点的指针指向要删除结点的孩子结点；
    3. 要删除的结点有左右两棵子树：用另一结点替代被删除的结点：可以使用右子树的最小元素，或者左子树的最大元素替代。
    BinTree Delete( BinTree BST, ElementType X ) 
{ 
    BinTree Tmp; 
 
    if( !BST ) 
        printf("要删除的元素未找到"); 
    else {
        if ( X < BST->Data ) // 如果该元素比当前结点小
            BST->Left = Delete( BST->Left, X ); // 从左子树递归删除
        else if ( X > BST->Data ) // 如果该元素比当前结点大
            BST->Right = Delete( BST->Right, X ); // 从右子树递归删除
        else // BST就是要删除的结点
        { 
            // 1、如果被删除结点有左右两个子结点
            if ( BST->Left && BST->Right ) 
            {
                // 从右子树中找最小的元素填充待删除结点
                Tmp = FindMin( BST->Right );
                BST->Data = Tmp->Data;
                // 从右子树中删除最小元素
                BST->Right = Delete( BST->Right, BST->Data );
            }
            else // 被删除结点有一个或无子结点
            { 
                Tmp = BST; 
                if(!BST->Left && !BST->Right)  // 没有孩子结点 
				    BST = NULL;
                else if ( BST->Right && !BST->Left ) // 只有右孩子
                    BST = BST->Right; // 将父结点指向该右子节点
                else if ( BST->Left && !BST->Right ) // 只有左孩子
                    BST = BST->Left;  // 将父结点指向该右子节点
                free( Tmp );
            }
        }
    }
    return BST;
}


    平衡二叉树

    定义

    平衡因子（Balance Tree, 简称BF）: (BF(T)=h_L-h_R)，其中(h_L)和(h_R)分别为T的左右子树的高度。

    平衡二叉树（Balanced Binary Tree, 或称AVL树）：
    空树，或者任意结点的左右子树高度差的绝对值不超过1，即(|BF(T)| le 1)。

    提问：
    平衡二叉树的高度能达到(log_2N)吗？

    设(N_h)高度为h的AVL树的最少结点数，结点最少时：

    • h = 0时，(N_h = 1)
    • h = 1时，(N_h = 2)
    • h = 2时，(N_h = 4)
    • h = 3时，(N_h = 7)
    • h = 4时，(N_h = 12)

    因此可以推出：(N_h = N_{h-1}+N_{h-2}+1)。类比于斐波拉契数列有：(N_h approx frac{1}{sqrt{5}}(frac{1+sqrt{5}}{2})^{h+2}-1)，即：

    [h = O(log_2N) ]

    结论：给定结点数为N的AVL树的最大高度为(O(log_2N))


    AVL的调整

    右单旋（RR旋转）

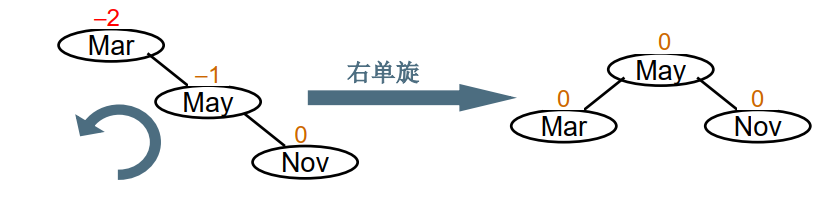
    不平衡的“发现者”是Mar，“麻烦结点”是Nov，在发现者右子树的右边，因而叫RR插入，此时Mar 的平衡因子BF=-2，为保持平衡，需要RR旋转。

    如图所示，基本思想是: 把B的左子树腾出来挂到A的右子树上，返回B作为当前子树的根


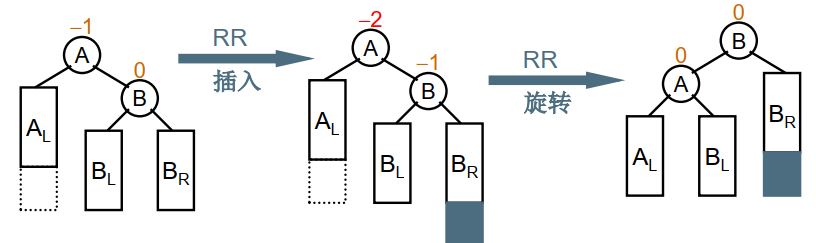
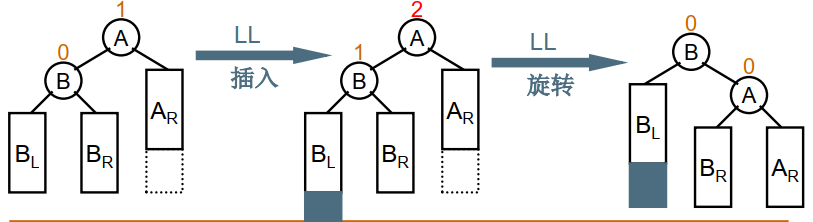
    左单旋（LL旋转）

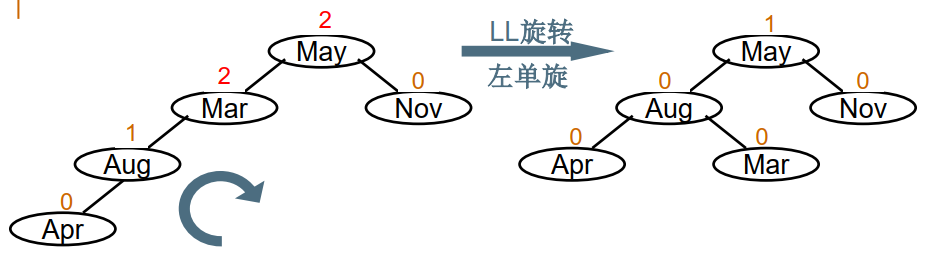
    不平衡的“发现者”是Mar，“麻烦结点”是Apr，在发现者左子树的左边，因而叫LL插入，此时Mar和May 的平衡因子BF=2，为保持平衡，需要LL旋转.

    如图所示，基本思想是: 把B的右子树腾出来挂到A的左子树上，返回B作为当前子树的根


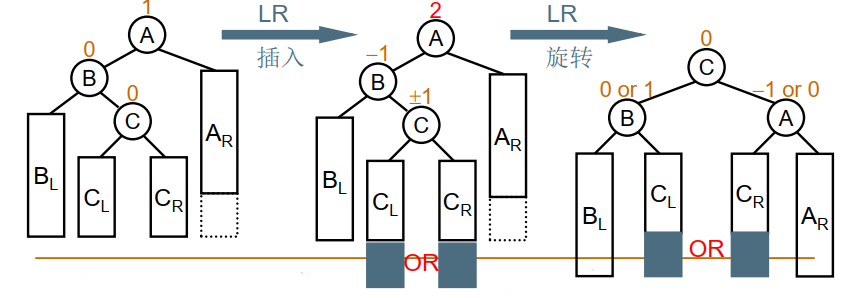
    左-右单旋（LR旋转）

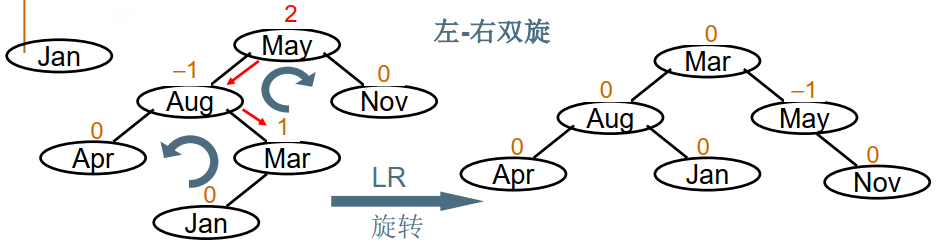
    不平衡的“发现者”是May，“麻烦结点”是Jan，在发现者左子树的右边，因而叫LR插入，需要LR旋转,即把Aug的右子树Mar,调整为根结点。

    如图所示，基本思想是：先将B作为根结点进行RR单旋转化为LL插入，再将A作为根结点进行LL单旋（先 RR 再 LL）


    右-左单旋（RL旋转）

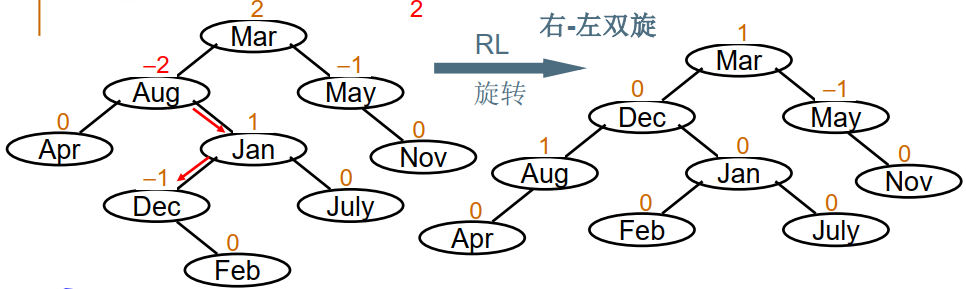
    不平衡的“发现者”是Aug，“麻烦结点”是Feb，在发现者右子树的左边，因而叫RL插入，需要RL旋转,即调整Jan的左子树Dec为Aug和Jan根结点.

    如图所示，基本思想是：先将B作为根结点进行LL单旋转化为RR插入，再将A作为根结点进行RR单旋（先 LL 再 RR）


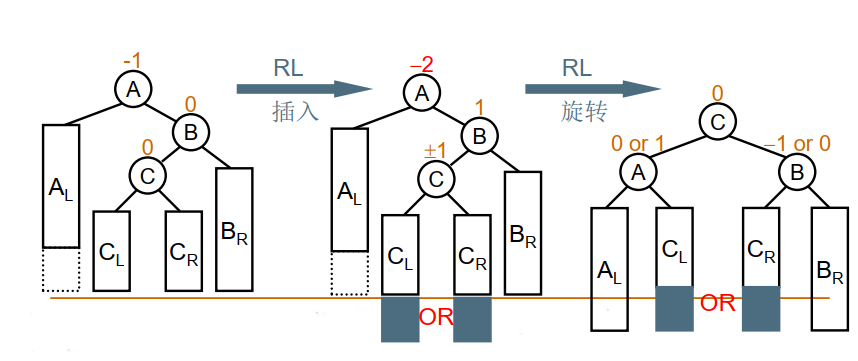
    程序实现：

    typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode
{
    ElementType Data; /* 结点数据 */
    AVLTree Left;     /* 指向左子树 */
    AVLTree Right;    /* 指向右子树 */
    int Height;       /* 树高 */
};
 
int Max ( int a, int b )
{
    return a > b ? a : b;
}

/* RR旋转 */
AVLTree SingleRightRotation ( AVLTree A )
{ 
    /* 注意：A必须有一个右子结点B */
    /* 将A与B做右单旋，更新A与B的高度，返回新的根结点B */     
 
    AVLTree B = A->Right;  // B为A的右子树 
    A->right = B->left;    // B的左子树挂在A的右子树上 
	B->left = A;           //  A挂在B的左子树上 
    A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
    B->Height = Max( GetHeight(B->Right), A->Height ) + 1;
 
    return B; // 此时B为根结点了 
}

/* LL旋转 */
AVLTree SingleLeftRotation ( AVLTree A )
{ 
    /* 注意：A必须有一个左子结点B */
    /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */     
 
    AVLTree B = A->Left;  // B为A的左子树  
    A->Left = B->Right;   // B的右子树挂在A的左子树上 
    B->Right = A;         // A挂在B的右子树上 
    A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
    B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
  
    return B;   // 此时B为根结点了 
}

/* LR旋转 */
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ 
    /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
    /* 将A、B与C做两次单旋，返回新的根结点C */
     
    /* 将B与C做右单旋，C被返回 */
    A->Left = SingleRightRotation(A->Left);
    /* 将A与C做左单旋，C被返回 */
    return SingleLeftRotation(A);
}

/* RL旋转 */
AVLTree DoubleRightLeftRotation ( AVLTree A )
{ 
    /* 注意：A必须有一个右子结点B，且B必须有一个左子结点C */
    /* 将A、B与C做两次单旋，返回新的根结点C */
     
    /* 将B与C做左单旋，C被返回 */
    A->Left = SingleLeftRotation(A->Right);
    /* 将A与C做右单旋，C被返回 */
    return SingleRightRotation(A);
}
 

AVLTree Insert( AVLTree T, ElementType X )
{ 
    /* 将X插入AVL树T中，并且返回调整后的AVL树 */
    if ( !T ) 
    { 
        /* 若插入空树，则新建包含一个结点的树 */
        T = (AVLTree)malloc(sizeof(struct AVLNode));
        T->Data = X;
        T->Height = 0;
        T->Left = T->Right = NULL;
    }
    else if ( X < T->Data ) 
    {
        /* 插入T的左子树 */
        T->Left = Insert( T->Left, X);
        /* 如果需要左旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
            if ( X < T->Left->Data ) 
               T = SingleLeftRotation(T);      /* 左单旋 */
            else 
               T = DoubleLeftRightRotation(T); /* 左-右双旋 */
    }
    else if ( X > T->Data ) 
    {
        /* 插入T的右子树 */
        T->Right = Insert( T->Right, X );
        /* 如果需要右旋 */
        if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
            if ( X > T->Right->Data ) 
               T = SingleRightRotation(T);     /* 右单旋 */
            else 
               T = DoubleRightLeftRotation(T); /* 右-左双旋 */
    }
    /* else X == T->Data，无须插入 */
 
    /* 别忘了更新树高 */
    T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
     
    return T;
}


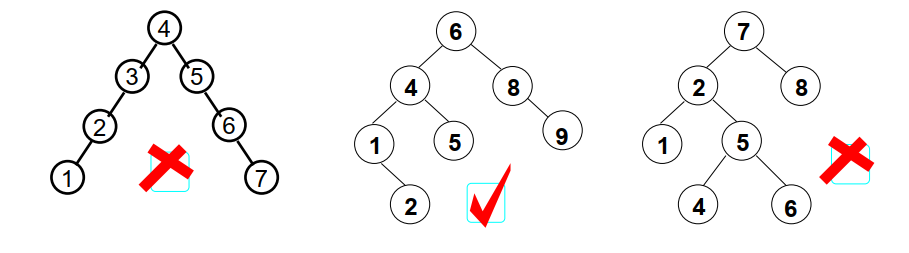
    应用：是否为同一颗二叉搜索树

    题意理解

    给定一个插入序列就可以唯一确定一棵二叉搜索树，然而一棵给定的二叉搜索树却可以由多种不同的插入序列得到。eg.序列{2,1,3}和{2,3,1}可以得到一样的结果。

    那么：对于输入的各种插入序列，你是否可以判断他们是否能生成一样的二叉搜索树。

    输入样例：

    • 4 2
    • 3 1 4 2
    • 3 4 1 2
    • 3 2 4 1

    第1行代表序列长度为4，且有2个待比较序列；第2行为序列原型，3,4行为具体的待比较序列。

    输出样例：

    • Yes
    • No

    求解思路

    1、分别建两棵搜索树

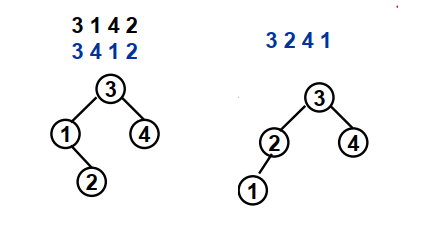
    fig4_6.png

    2、不建树

    fig4_7.PNG

    3、建一棵树，再判别其他序列是否与该树一致

    1. 搜索树表示；
    2. 建搜索树T;
    3. 判别一序列是否与搜索树T一致

    程序框架

    int main()
{
    对每组数据：
    1、读入N和L；
    2、根据第一行序列建树T
    3、根据树T分别判别后面
    的L个序列是否能与T形成
    同一搜索树并输出结果
    return 0;
}

    程序实现

    #include <stdio.h>
#include <stdlib.h>  //调用malloc()和free()
#include <windows.h> //windows.h里定义了关于创建窗口，消息循环等函数S

typedef struct TreeNode *Tree;
struct TreeNode
{
    int data;
    Tree Left, Right;
    int flag;  // flag=1代表结点已被查找，flag=0代表结点还未被查找
};

/* 函数声明 */
Tree Insert(Tree T, int X); // BST插入新结点
Tree MakeTree(int N);       // 构建结点数为N的BST
Tree NewNode(int X);        // 构建根结点为X的BST
int check(Tree T, int X);   // 在T中判断X是否被查找标记
int Judge(Tree T, int N);   // 判断长度为N的序列是否与BST一致
void ResetT(Tree T);        // 清除T中的标记flag
void FreeTree(Tree T);      // 清除T中各结点的flag标记

/* 主函数入口 */
int main()
{
    int N, L, i;
    Tree T;
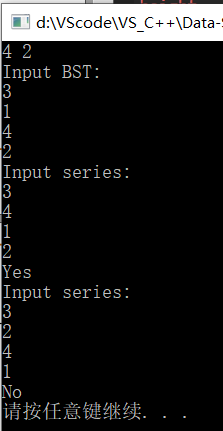
    scanf("%d %d", &N, &L);
    printf("Input BST:
");
    T = MakeTree(N);
    for (i = 0; i < L; i++)
    {
        printf("Input series:
");
        if (Judge(T, N))
            printf("Yes
");
        else
            printf("No
");
        ResetT(T); //清除T中的标记flag
    }

    /*
    scanf("%d", &N);
    while (N)
    {
        scanf("%d", &L);
        T = MakeTree(N);
        for (i = 0; i < L; i++)
        {
            if (Judge(T, N))
                printf("Yes
");
            else
                printf("No
");
            ResetT(T);    //清除T中的标记flag
        }

        FreeTree(T);
        scanf("%d", &N);
    }*/

    system("pause"); //程序暂停，显示按下任意键继续
    return 0;
}


/* 在二叉搜索树中插入新结点 */
Tree Insert(Tree T, int X)
{
    if (!T)
        T = NewNode(X);
    else
    {
        if (X > T->data)
            T->Right = Insert(T->Right, X);
        else
            T->Left = Insert(T->Left, X);
    }
    return T;
}

/* 构建结点数为N的BST */
Tree MakeTree(int N)
{
    Tree T;
    int i, X;
    scanf("%d", &X);
    T = NewNode(X);
    for (i = 1; i < N; i++)
    {
        scanf("%d", &X);
        T = Insert(T, X);
    }
    return T;
}

/* 构建根结点为X的BST */
Tree NewNode(int X)
{
    Tree T = (Tree)malloc(sizeof(struct TreeNode));
    T->data = X;
    T->Left = T->Right = NULL;
    T->flag = 0;
    return T;
}

/* 在T中判断X是否被查找标记，成功返回1，失败返回0 */
int check(Tree T, int X)
{
    if (T->flag) // flag=0，根结点已被访问
    {
        if (X < T->data)
            return check(T->Left, X);
        else if (X > T->data)
            return check(T->Right, X);
        else  // 如果此时X仍等于根结点的值，则代表有两个值等于根结点，此时一定不一致
            return 0;
    }
    else // flag=0，根结点还未被访问
    {
        if (X == T->data) // 如果待插入的结点等于T结点的值，则将此结点的flag标记为1
        {
            T->flag = 1;
            return 1;
        }
        else // 若待插入的结点不等于T结点的值，则代表碰到了之前没见过的结点，此时序列构成的BST一定不一致
            return 0;
    }
}

/* 判断长度为N的序列是否与BST一致，成功返回1，失败返回0 */
int Judge(Tree T, int N)
{
    int i, V, Tag = 0;
    /* flag: 0代表目前还一致， 1代表已经不一致*/
    scanf("%d", &V);
    // 1、首先比较输入值与当前树树根的值是否一致
    if (V != T->data)
        Tag = 1;
    else
        T->flag = 1;
    
    // 2、逐个查找序列中的N-1个数，是否能成功查找标记
    for (i = 1; i < N; i++)
    {
        scanf("%d", &V);
        if ((!Tag) && (!check(T, V)))
            Tag = 1;
    }
    if (Tag) // 若tag=1,则代表序列中有某个值未能成功标记
        return 0;
    else     // tag=0,代表序列的N个值均能在BST中成功标记
        return 1;
}

/* 清除T中各结点的flag标记 */
void ResetT(Tree T)
{
    if (T->Left)
        ResetT(T->Left);
    if (T->Right)
        ResetT(T->Right);
    T->flag = 0;
}

/* 释放T的空间 */
void FreeTree(Tree T)
{
    if (T->Left)
        FreeTree(T->Left);
    if (T->Right)
        FreeTree(T->Right);
    free(T);
}

    运行结果：
  • 相关阅读:
    阅读笔记03
    第十三周总结
    阅读笔记02
    第十二周总结
    第十一周总结
    阅读笔记01
    阅读笔记3
    第十一周总结
    阅读笔记
    HDFS-学习总结
  • 原文地址：https://www.cnblogs.com/Superorange/p/12527336.html
Copyright © 2020-2023  润新知