【IOI】2007 训练路径

树形dp+状压dp

题目链接

首先，无法删的边会形成一棵树（废话）

那么我们把这棵树先弄出来。

由于

为了保证他们的训练强度相同，他们要选择一条具有偶数条道路的路径。

因此剩下的非树边两端点构成了一个偶环，那么这条非树边是肯定要删除的。

又因为

绝不中途穿越已经去过的城市，并且绝不在相同的道路上骑行两次（不管方向是否相同）

那么在删去会形成偶环的非树边后，我们可以发现，如果有两个奇环的树边是相重的，显然也是不合法的。

因此，每条树边最多只会被遍历到一次。

那么，我们可以倒过来弄。即选择若干条非树边，使得每条树边最多只会遍历到一次，且使得这些边权尽可能大。

再看一次题目

此外，每个城市最多是101010条道路的端点

对此，考虑状压：(dp[x][sta])表示当前节点为x，其儿子被选择的状态为sta（1表示被选）的最大边权和。

那么对于一条非树边，有两种决策：

1.选它。（见图解）

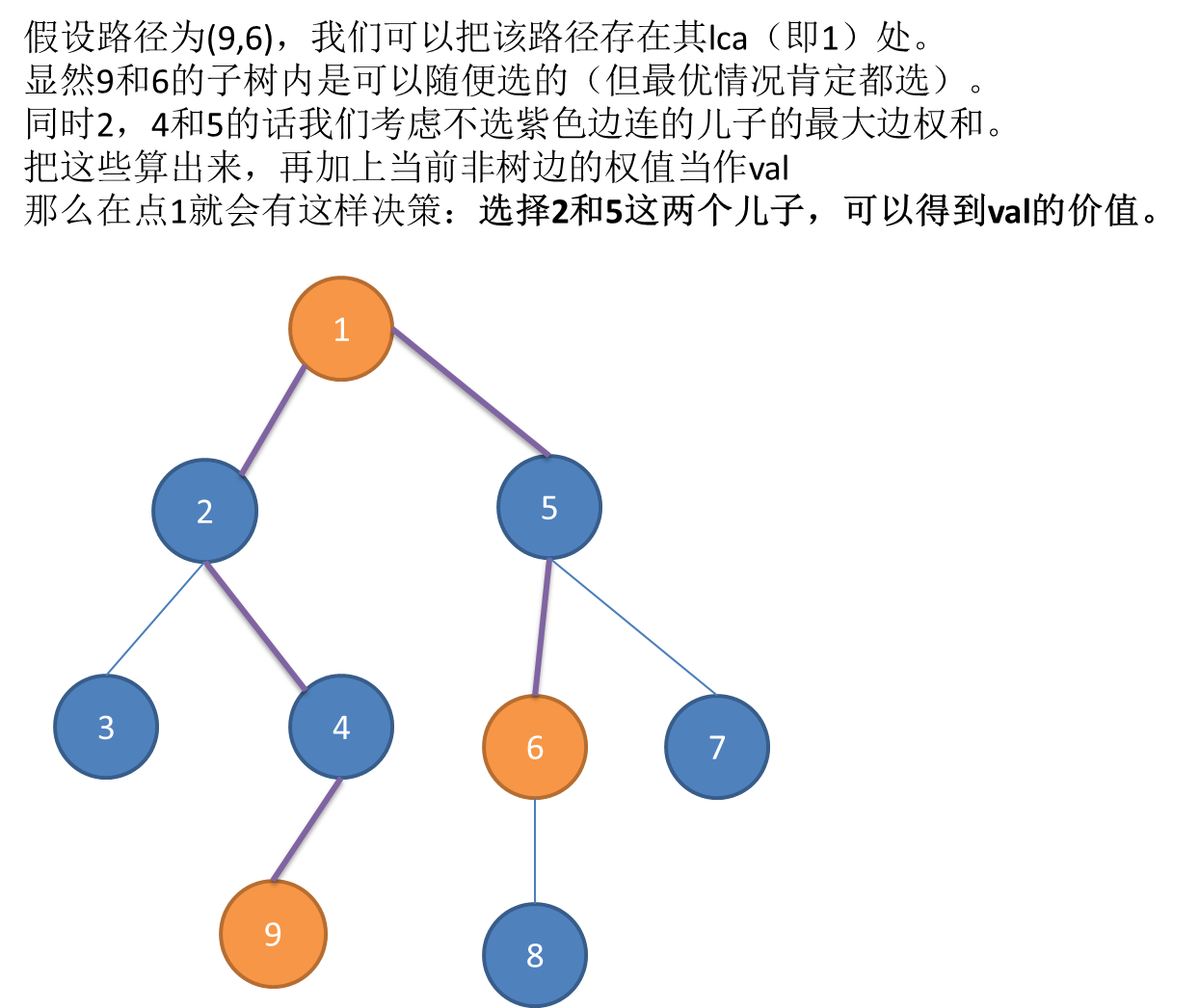
也就是说，当回溯到一个点时，我们取出以它为lca的所有非树边，然后蜗牛爬式的预处理val（反正n才1000）

然后转移一下就好了。

2.不选它。

这个就比较easy了。

对于一个状态sta，我们只需查找被选的儿子，然后把这些儿子的dp值累和弄过来就可以了。

代码:

#include<bits/stdc++.h>
#define MAXN 10010
using namespace std;
int n,m,tot,head[MAXN],cnt,pre[MAXN][20],deep[MAXN],lg[MAXN],dp[1050][1050],num[1010][1010],Cnt[MAXN],ansSum,ans;
struct sgt {
	int st,ed,v,lca,sum,X,Y;
} E[MAXN];
struct node {
	int ed,last;
} G[MAXN<<1];
vector<int> Q[MAXN];
void Add(int st,int ed) {
	tot++;
	G[tot]=node {ed,head[st]};
	head[st]=tot;
}
void DFS(int x,int fa){
	deep[x]=deep[fa]+1;
	pre[x][0]=fa;
	for(int i=1;(1<<i)<=deep[x];i++)pre[x][i]=pre[pre[x][i-1]][i-1];
	for(int i=head[x];i;i=G[i].last){
		int t=G[i].ed;
		if(t==fa)continue;
		DFS(t,x);
	}
}
int LCA(int x,int y){
	if(deep[x]<deep[y])swap(x,y);
	while(deep[x]>deep[y])x=pre[x][lg[deep[x]-deep[y]]-1];
	if(x==y)return x;
	for(int i=lg[deep[x]]-1;i>=0;i--){
		if(pre[x][i]==pre[y][i])continue;
		x=pre[x][i],y=pre[y][i];
	}
	return pre[x][0];
}
int jump(int x,int y,int id){
	if(x==y)return 0;
	int sonx=x;
	x=pre[x][0];
	while(x!=y){
		E[id].sum+=dp[x][((1<<Cnt[x])-1)^num[x][sonx]];
		sonx=x;
		x=pre[x][0];
	}
	return sonx;
}
void solve(int x,int fa){
	for(int i=head[x];i;i=G[i].last){
		int t=G[i].ed;
		if(t==fa)continue;
		num[x][t]=1<<Cnt[x];
		Cnt[x]++;
		solve(t,x);
	}
	for(int i=0;i<Q[x].size();i++){
		int id=Q[x][i],st=E[id].st,ed=E[id].ed;
		E[id].sum=dp[st][(1<<Cnt[st])-1]+dp[ed][(1<<Cnt[ed])-1]+E[id].v;
		E[id].X=jump(st,x,id);
		E[id].Y=jump(ed,x,id);
	}
	for(int i=0;i<(1<<Cnt[x]);i++){
		int res=0;
		for(int j=head[x];j;j=G[j].last){
			int t=G[j].ed;
			if(t==fa)continue;
			if(num[x][t]&i)res+=dp[t][(1<<Cnt[t])-1];
		}
		dp[x][i]=max(dp[x][i],res);
	}
	for(int i=0;i<(1<<Cnt[x]);i++){
		for(int j=0;j<Q[x].size();j++){
			int id=Q[x][j],X=E[id].X,Y=E[id].Y;
			if((num[x][X]&i)||(num[x][Y]&i))continue;
			dp[x][i|num[x][X]|num[x][Y]]=max(dp[x][i|num[x][X]|num[x][Y]],dp[x][i]+E[id].sum);
		}
	}
}
int main() {
	for(int i=1;i<=MAXN-10;i++)lg[i]=lg[i-1]+((1<<lg[i-1])==i);
	scanf("%d %d",&n,&m);
	for(int x,y,z,i=1; i<=m; i++) {
		scanf("%d %d %d",&x,&y,&z);
		if(z==0) {
			Add(x,y);
			Add(y,x);
		}
		else {
			cnt++;
			E[cnt]=sgt{x,y,z};
		}
	}
	DFS(1,0);
	for(int i=1;i<=cnt;i++){
		E[i].lca=LCA(E[i].st,E[i].ed);
		if((deep[E[i].st]+deep[E[i].ed]-2*deep[E[i].lca])&1)ans+=E[i].v;	
		else Q[E[i].lca].push_back(i),ansSum+=E[i].v;
	}
	solve(1,0);
	ans+=ansSum-dp[1][(1<<Cnt[1])-1];
	cout<<ans;
	return 0;
}