单位向量
在计算机图形学中单位向量的使用极为普遍,例如表面的法线向量、切线向量和光线相关的向量等。这样一来,很多的图形学的算法的时间&空间性能都取决于针对这些向量的读取、处理和写入的速度。
特别的是传输这些数据的带宽需求与G-buffer对于内存的需求在很多地方制约了GPU渲染的速度。
在现在的图形渲染管线中,3D的向量要么存在高带宽的寄存器(registers)中,要么存在中等带宽的计算机内存中,要么存在低带宽的磁盘中。针对于单位向量,寄存器由于对速度有着极高的要求,往往希望你能够将其以float32*3的形式进行单位向量的储存,而磁盘往往更希望更有效地利用存储空间,因此会鼓励你进行各种的编码/解码操作。
但是针对于在内存(或者芯片上的cache)中的存储,往往需要在速度和存储空间上取得一个平衡。因此可以考虑将单位向量进行某种程度的编码和解码,当然这种编码和解码也不能太复杂或者损失太多信息。
正常的表现方法以及分析
先看看单位向量的最普通的表现方法:一个包含三个32-bit的浮点数的结构体:
1 struct{float x, y, z;}
那么它所占用的储存空间为:3∗4∗8=963∗4∗8=96bits。
可知的是,这种表现方法的域实际上是整个3D空间,R3ℜ3,换句话说就是从原点到无穷远处(也不尽然……32位浮点数也有范围)的空间。
但是正常的单位向量的域却是位于原点,半径为1的球面。
这就意味着这96-bit位的模版中有绝大部分的实例针对于表现单位向量是不起任何作用的。换句话说,资源浪费了不少。
就存储空间来说,完美的模版则应该是每一种实例都能够表现这个球面上的唯一的一个点
Easy的优化算法
有一种容易想到的算法是使用球面坐标,也就是存储两个32-bit的浮点数用于存储该向量在三维坐标系中的角度。
转化为八面体的算法
有一种可行的算法是将整个球面上的点先投影至一个八面体中,然后再投影到z=0的平面上,但是针对于那些Z<0的点,进行对折。从而将圆的点映射到一个平面上,该平面为长宽为2的正方形,过程图如下:
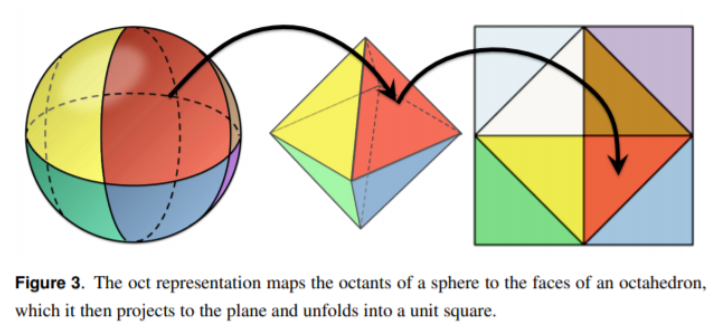
这样一来,我们只需要储存对应的(u,v)(u,v)坐标即可。
我们认为这种方法相对来讲是最好的:编码解码的计算过程简单,而且基本上也是平均的分布。
针对于这种向量进行编码的方式叫做“Octahedral Normal Vectors (ONV),”这种方法相对来讲高效且优雅,并且误差也较小。
上面提到计算过程简单的原因其实一开始我也没想明白,而且也计算了好一会。但是后来发现在真正的实现中也并没有按照完全的几何结果来计算,而是粗暴的将L2L2(欧几里德范数)代替为L1L1(曼哈顿范数),从而得到一个近似的解。
按照上面的方法来实现的话,那么对应的编码和解码如下:
1 float2 UnitVectorToOctahedron( float3 N ) 2 { 3 N.xy /= dot( 1, abs(N) ); 4 if( N.z <= 0 ) 5 { 6 N.xy = ( 1 - abs(N.yx) ) * ( N.xy >= 0 ? float2(1,1) : float2(-1,-1) ); 7 } 8 return N.xy; 9 } 10 11 float3 OctahedronToUnitVector( float2 Oct ) 12 { 13 float3 N = float3( Oct, 1 - dot( 1, abs(Oct) ) ); 14 if( N.z < 0 ) 15 { 16 N.xy = ( 1 - abs(N.yx) ) * ( N.xy >= 0 ? float2(1,1) : float2(-1,-1) ); 17 } 18 return normalize(N); 19 }
需要注意的是shader里 关于符号判断的三目表达式是重载了的,x和y是分别来比的。所以如果在cpu端实现这段代码,那么16行正确的的做法应该是
N.xy = ( 1 - abs(N.yx) ) * ( N.x >= 0 ? 1 : -1, N.y >= 0 ? 1 : -1);