也许分块我还是能行的
大概就是把数据分成几块来使查询变快,修改变慢,均摊时间复杂度(O(sqrt{n}))的算法。
分成几块呢?如果按两个一块分,查询时间复杂度只能降到之前的1/2,要是分成n个一块查询时间复杂度会退化成原时间复杂度(仅一个例外,1-n的查询是(O(1))),修改时间复杂度是(O(n))。
为了保持优秀的时间复杂度,我们按(sqrt{n})大小一块,能够使均摊时间复杂度变成(O(sqrt{n}))(查询时间复杂度同修改时间复杂度同均摊复杂度)。
原理上,分块就是把数据分成几块,预先处理出每块里面需要查询的数据的总值(和就是该区间内的全部元素和,积或者其他什么东西的总*),然后在查询时,对该区间内的整块,直接用该区间内的总*,对于不满一块的暴力处理单个元素就行了。
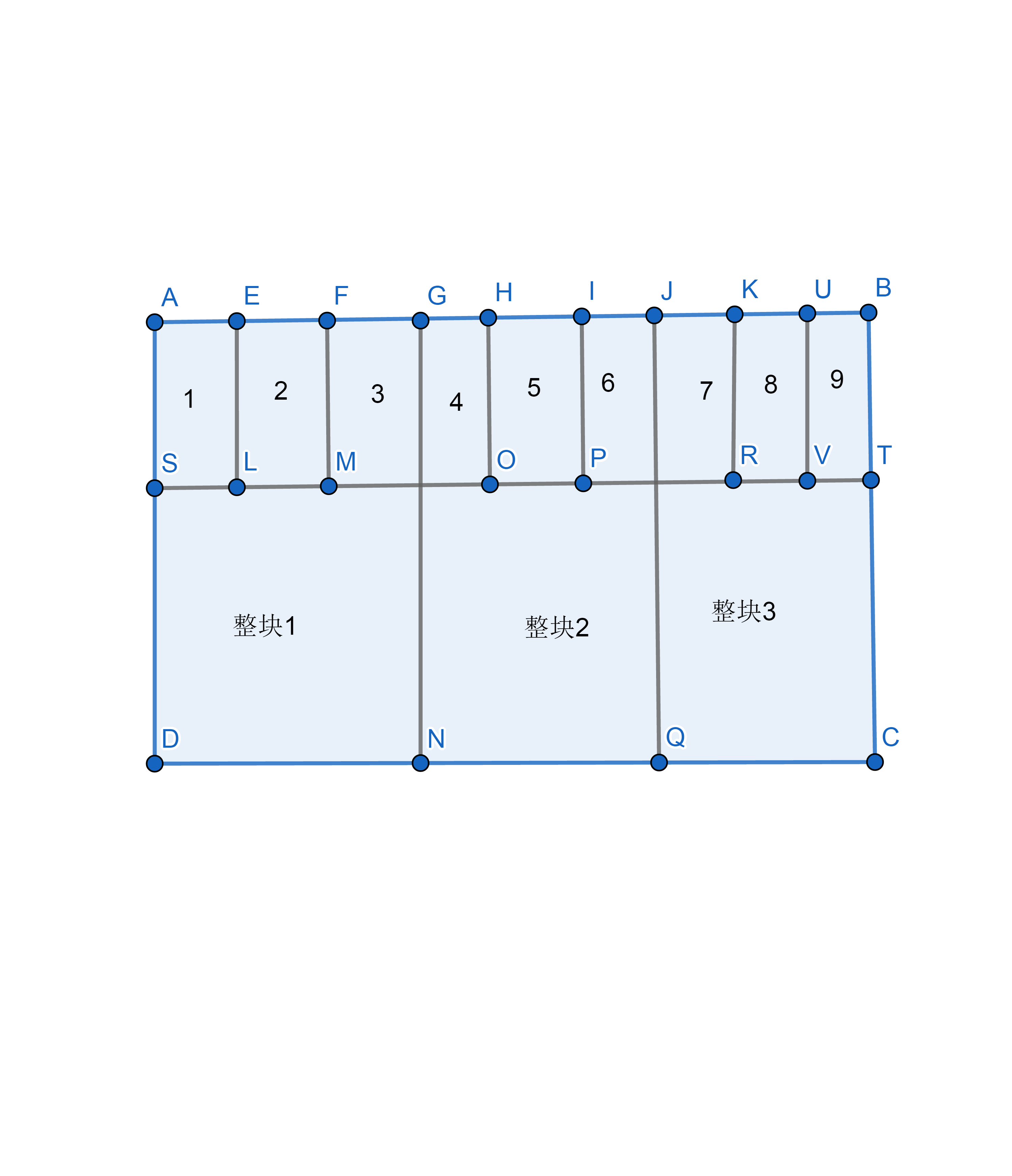
如上图,这是一种分块的方式。
然后如果我们有几个例题:
- 给定数列,要求查询给定区间[ l , r ]的区间和。
好像用前缀和就能做?可是前缀和虽然查询很快,但是不支持修改,修改的时间复杂度为(O(n))。
在使用分块时,讲区间分成根号r-l块,对于每块预先处理出每块的和,如果查询的区间中包含整块直接将答案加上整块的和,不满一块则对于单个元素直接暴力求和。 - 给定数列,要求查询给定区间[ l , r ]的区间积。
这次不能用前缀积了,像上面那样,预先处理出每块的积,不满一块的暴力乘上去。 - 给定数列,要求查询给定区间[ l , r ]的区间最值。
听说能用ST表,能达到查询(O(1))的速度,但我不知道支不支持修改。
预先处理出每块的最值,不满一块的暴力求最值。
分块有常数(什么没有常数),最坏常数大概在4,最好常数1。
其他什么寻找区间内前驱后继的还有什么莫队的,我不懂啊。