Description

题解
题目说这是一个具有神奇特性的数列!这句话是非常有用的因为我们发现,如果套着这个数列的定义再从原数列引出一个新数列,它居然还是一样的......
于是我们就想到了能不能用多点数列套着来加速转移呢?
但是发现好像太多数列套起来是可以烦死人的......
我们就采用嵌套两次吧(第三次以后规律就不明显了),记原数列为A,第一层嵌套为B,第二层嵌套为C。
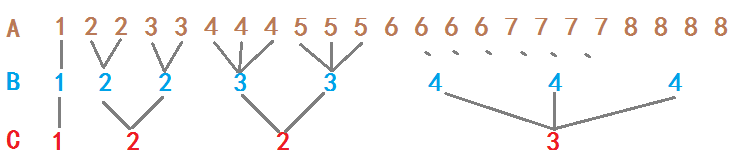
我们其实可以发现一些规律,对于Ci,它对应了B中i的个数;对于Bi,它对应了A中i的个数。
稍加处理即可,我们一边计算一边模拟数列的运算,同时可以计算实际上在A中前进的步数,如果超过了n就暴力模拟退格。
时间复杂度???极快
PS: 原先写了一个很慢的预处理程序,本地正常编译,对拍没问题;结果上去给OJ的O2卡了我的 用常数做上限的数组的循环到上限的语句gg。(其实还是被空间限制卡掉了1个点......)

1 #include <cstdio> 2 using namespace std; 3 typedef long long ll; 4 const int N=20000010; 5 ll n,sum,id,end,lis[N]; 6 int main(){ 7 scanf("%lld",&n); 8 lis[1]=lis[2]=1; 9 end=id=sum=1; 10 for(int i=2;;i++) 11 for(int j=1;j<=lis[i];j++){ 12 lis[++end]=i; 13 sum+=end*i; 14 id+=i; 15 if(sum<n) continue; 16 while(sum-end>=n) 17 id--,sum-=end; 18 printf("%lld ",id); 19 return 0; 20 } 21 return 0; 22 }
注意处理一些细节,比如初始各变量的值(lis[2]=1实际上是为了顺利进入循环而已)。
