Representation revisited
Knowledge representation languages should be declarative, compositional, expressive, context independent, and unambiguous.
2. Combining the best of formal and natural languages
Objects: Nouns and noun phrases refer to objects. (e.g. people, houses, number, theories…)
Relations: Verbs and verb phrases refer to relations among objects.
Relations can be unary relations or properties (e.g. red, round, bogus, prime …), or more general n-ary relations (e.g. brother of, bigger than, inside, part of, has color, occurred after, owns, comes between, …).
Function: some relations in which there is only one “value” for a given “input”. (e.g. father of, best friend, third inning of, one more than, beginning of … ).
Almost any assertion can be thought of as referring to objects and properties or relations.
Logics differ in their ontological commitments and epistemological commitments. While propositional logic commits only to the existence of facts, first-order logic commits to the existence of objects and relations and thereby gain expressive power.
The primary difference between propositional and first-order logic lies in the ontological commitment made by each language.
Ontological commitment: What it assumes about the nature of reality. Mathematically the ontological commitment is expressed through the nature of the formal models with respect to which the truth of sentences is defined.
Propositional logic assumes that there are facts that either hold or do not hold in the world. Each fact can be in one of two states: true or false, and each model assigns true or false to each proposition symbol.
First-order logic assumes that the world consists of objects with certain relations among them that do or do not hold. The formal models are correspondingly more complicated than those for propositional logic.
Higher-order logic views the relations and functions referred to by first-order logic as objects in themselves. Higher-order logic is strictly more expressive than first-order logic, some sentences of higher-order logic cannot be expressed by any finite number of first-order logic sentences.
Epistemological commitments: The possible states of knowledge that a logic allows with respect to each fact.
Both propositional logic and first-order logic have 3 possible states of knowledge regarding any sentence, a sentence represents a fact and the agent either believes the sentence to be true, believes it to be false, or has no opinion.
System using probability theory can have any degree of belief, ranging from 0 (total disbelief) to 1 (total belief).
Syntax and semantics of first-order logic
1. Models for first-order logic
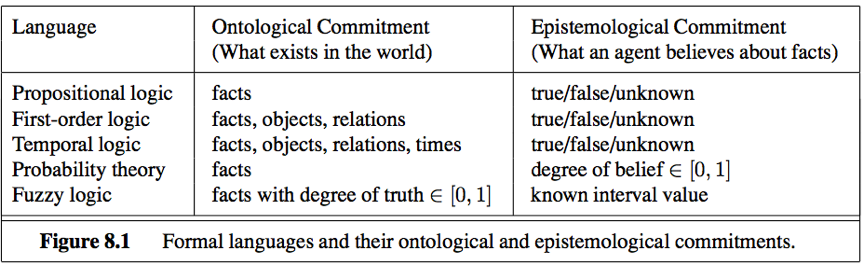
Domain: The domain of a model is the set of objects or domain elements in contains. The domain is required to be nonempty. (every possible world must contain at least one objects)
Tuple: A collection of objects arranged in a fixed order and is written with angle brackets surrounding the objects.
Relation: A set of tuples of objects that are related.
Binary relation: relates pairs of objects.
Function: Certain kinds of relationships are best considered as functions, in that a given object must be related to exactly one object in this way.
e.g.
The “brotherhood” relation is
{ <Richard the Lionheart, King John>, <King John, Richard the Lionheart> }.
The “on head” relation is
{ <the crown, King John> }.
Binary relations: the “brotherhood” relation, the “on head” relation.
Unary relations/properties: The “person” property (true of both Richard and John), the “king” property (true only of John), the “crown” property (true only of the crown).
The unary “left leg” function includes the following mappings:
<Richard the Lionheart> → Richard’s left leg
<King John> → John’s left leg.
Strictly speaking, models in first order logic require total functions, i.e. there must be a value for every input tuple.
2. Symbols and interpretations

A possible world, or model, for first-order logic includes a set of objects and an interpretation that maps constant symbols to objects, predicate symbols to relations among objects, and function symbols to functions on objects.
Symbols: Basic syntactic elements of first-order logic, stand for objects, relations and functions.
The symbols come in 3 kinds: constant symbols, which stand for objects; predicate symbols, which stand for relations; and function symbols, which stand for functions.
Each predicate and function symbol comes with an arity that fixes the number of argument.
Interpretation: Each model includes an interpretation that specifies exactly which objects, relations and functions are referred to by the constant, predicate, and function symbols.
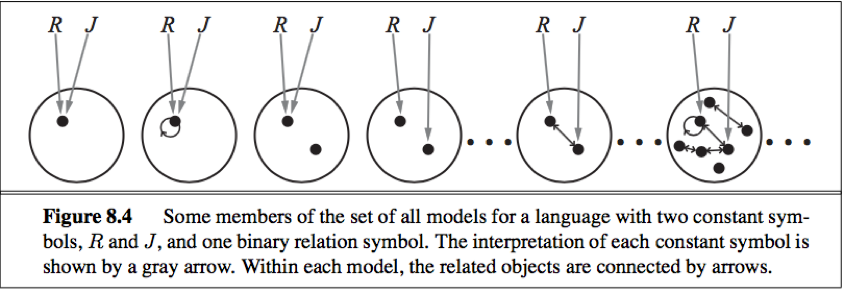
Entailment, validity and so on are defined in terms of all possible models. Models vary in how many objects they contain (from one up to infinity) and in the way the constant symbols map to objects.
Because the number of possible models is unbounded, checking entailment by the enumeration of all possible models is not feasible for first-order logic. Even if the number of objects is restricted, the number of combinations can be very large.
3. Terms
Term: A term is a logical expression that refers to an object.
In the genral case, a complex term is formed by a function symbol followed by a parenthesized list of term as arguments to the function symbols. E.g. LeftLeg(John)
A complex term is just a complicated kind of name, not a “subroutine call” that “returns a value”.
The semantics of terms:
Consider a term: f ( t1, …, tn ).
The function symbol f refers to some function F in the model;
The argument terms t1, …, tn refer to objects in the domain d1, …, dn;
The term as a whole refers to the objects that is the value of the function F applied to d1, …, dn.
4. Atomic sentences
Atomic sentence: An atomic sentence (for atom) is formed from a predicate symbol optionally followed by a parenthesized list of terms.
e.g.
Brother (Richard, John)
states that Richard is the brother of John.
Atomic sentences can have complex terms as arguments.
e.g.
Married (Father(Richard), Mother(John))
states that Richard’s father is married to John’s mother.
An atomic sentence is true in a given model if the relation referred by the predicate symbols among the objects referred to by the arguments.
An atomic sentence is true just when the relation named by the predicate holds between the objects named by the terms.
5. Complex sentences
We can use logical connectives to construct complex sentences.
6. Quantifiers
First-order logic contains 2 standard quantifiers, universal and extential.
Universal quantification (∀)
Extended interpretations, which map quantifier variables to objects in the model, define the truth of quantified sentences.
∀x P is true in a given model if P is true in all possible extended interpretations constructed from the interpretation given in the model, where each extended interpretation specifies a domain element to which x refers.
e.g.
∀King(x) ⇒ Person(x).
We can extend the interpretation in 5 ways:
x → Richard the Lionheart,
x → King John,
x → Richard’s left leg,
x → John’s left leg,
x → the crown.
The universally quantified sentence ∀King(x) ⇒ Person(x) is true in the model if the sentence is true under each of the 5 extended interpretations.
The symbol x is called a variable, a variable is a term by itself, and can also serve as the argument of a function.
A term with no variables is called a ground term.
⇒ is the natural connective to use with ∀.
Existential quantification (∃)
∃x P is true in a given model if P is true in at least one extended interpretation that assigns x to a domain element.
e.g.
∃x Crown(x) ∧ OnHead(x, John).
The existential quantification ∃x Crown(x) ∧ OnHead(x, John) is true in the model if the sentence is true under at least one of the 5 extended interpretations.
∧ is the natural connective to use with ∃.
Nested quantifiers
Consecutive quantifiers of the same type can be written as one quantifier with several variables.
e.g.
∀x ∀y Brother(x, y) ⇒ Sibling(x, y)
can be written as
∀x, y Brother(x, y) ⇒ Sibling(x, y).
The order of quantification is important.
When two quantifiers are used with the same variable name, some confusion can arise.
The rule is that the variable belongs to the innermost quantifier that mentions it, then it will not be subject to any other quantification.
e.g.
∀x (Crown(x)∨(∃x Brother(Richard, x)))
can be written as
∀x (Crown(x)∨(∃z Brother(Richard, z))).
We will always use different variable names with nested quantifiers to avoid confusion.
Connection between ∀ and ∃
The De Morgan rules for quantified and unquantified sentences:
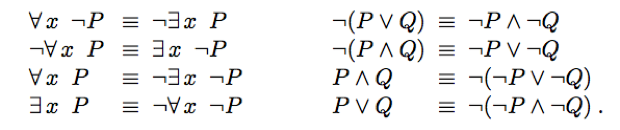
7. Equality
We can use the equality symbol to signify that two terms refer to the same object.
The equality symbol can be used to state fact about a given function.
e.g.
Father(John) = Henry
The equality symbol can be used with negation to insist that two terms are not the same object.
e.g. to say that Richard has at least two brothers, we write
∃x, y Brother(x, Richard)∧Brother(y, Richard)∧¬(x = y).
8. An alternative semantics?
Database semantics: Distinguished from the standard semantics of first-order logic, allows a more straightforward logical expression. Database semantics adopt:
Unique-names assumption: Insist that every constant symbol refer to a distinct object.
Closed-world assumption: Assume that atomic sentences not known to be true are in fact false.
Domain closure: Each model contains no more domain elements than those named by the constant symbols.
e.g. To state that Richard has two brothers, john and Geoffrey.
In first-order logic:
Brother(John, Richard)∧Brother(Geoffrey, Richard)∧John≠Geoffrey
∧∀x Brother(x, Richard)⇒(x=John∨x=Geoffrey)
In database semantics:
Brother(John, Richard)∧Brother(Geoffrey, Richard).
Using first-order logic
1. Assertions and queries in first-order logic
Assertions: Sentences added to a knowledge base using TELL (exactly as in propositional logic).
e.g. Assert that John is a king.
TELL (KB, King(John)).
Queries/goals: Questions asked with ASK. Any query that is logically entailed by the knowledge base should be answered affirmatively (true).
e.g.
ASK (KB, King(John)).
If we want to know what value of x makes the sentence true, call function ASKVARS, and it will yield a stream of answers. Such an answer is called a substitution or binding list.
e.g.
ASKVARS (KB, Person(x)).
Yield 2 answers: { x/John } and { x/Richard }.
ASKVAR is usually reserved for KBs consisting solely of Horn clauses, because in such KBs every way of making the query true will bind the variables to specific values. That is not the case with first-order logic.
2. The kinship domain
(Example of the kinship domain in first-order logic)
Axiom: A sentence that is taken as given without being derived from other sentences. (as in “Knowledge-based agents”)
Axioms can also be “just plain facts” that form the description of specific problem instances, enabling specific questions to be answered.
Definition: Axioms that have the form ∀x,y P(x, y) ⇔ …. , bottoms out at a basic set of predicates in terms of which the others are ultimately defined. (There is not necessarily a unique set of primitive predicates.)
Not all axioms are definitions.
Theorems: Logical sentences entailed by the axioms.
3. Numbers, sets, and lists
(Example of numbers, sets and lists domains in first-order logic)
Syntactic sugar: An extension to or abbreviation of the standard syntax that does not change the semantics. Any sentence that uses sugear can be “desugared” to produce an equivalent sentence in ordinary first-order logic.
4. The wumpus world
(Example of the wumpus world domain in first-order logic)
The corresponding first-order sentence stored in KB must include both the percept and the time at which it occurred.
The raw percept data implies certain facts about the current states, these rules exhibit a trivial form of the reasoning process called perception.
e.g.
∀t, s, g, m, c Percept([s, Breeze, g, m, c], t) ⇒ Breeze(t),
∀t, s, g, m, c Percept([s, Glitter, g, m, c], t) ⇒ Glitter(t).
Notice the quantification over time t.(In proposition logic we need copies of each sentence for each time step.)
Knowledge engineering in first-order logic
Developing a knowledge base in first-order logic requires a careful process of analyzing the domain, choosing a vocabulary, and encoding the axioms required to support the desired inferences.
Knowledge engineering: The general process of knowledge-base construction. A knowledge engineer investigates a particular domain, learns what concepts are important in that domain, and creates a formal representation of the objects and relations in the domain. (suitable for developing special-purpose knowledge bases)
Special-purpose knowledge bases: Knowledge bases whose domain is carefully circumscribed and whose range of queries is known in advance.
General-purpose knowledge bases: Knowledge bases which cover a broad range of human knowledge and are intended to support tasks such as language understanding.
1. The knowledge-engineering process
All knowledge engineering projects include the following steps:
1. Identify the task: To determine what knowledge must be represented in order to connect problem instances to answers. (analogous to the PEAS process)
2. Assemble the relevant knowledge: To understand the scope of the knowledge base, as determined by the task, and to understand how the domain actually works.
Knowledge acquisition: The process of work with real experts to extract what they know.
3. Decide on a vocabulary of predicates, functions and constants: To translate the important domain-level concepts into logic-level names, the result is a vocabulary that is known as the ontology of the domain. The ontology determines what kinds of things exist, but does not determine their specific properties and interrelationships.
4. Encode general knowledge about the domain: To write down the axioms for all the vocabulary terms, thus pin down the meaning of the terms and enable to expert to check the content.
5. Encode a description of the specific problem instance: To write simple atomic sentences about instances of specific problem (concepts that are already part of the ontology). For a logical agent, problem instances are supplied by the sensors, whereas a “disembodied” knowledge base is supplied with additional sentences in the same way that traditional programs are supplied with input data.
6. Pose queries to the inference procedure and get answers: To let the inference procedure operate on the axioms and problem-specific facts to derive the facts we are interested in knowing.
7. Debug the knowledge base: Missing axioms or axioms that are too weak can be easily identified by noticing places where the chain of reasoning stops unexpectedly.
2. The electronic circuits domain
(Example of “developing an ontology and knowledge base of the electronic circuits domain”)