CF566ERestoring Map【bitset】

正题

题目链接:https://www.luogu.com.cn/problem/CF566E

---

题目大意

有一棵树，但是你不知道它的形态。你现在只知道距离每个点距离不超过\(2\)的点集，但是你不知道每个点集是对应哪个点的。

现在要你求这棵树。

\(2\leq n\leq 1000\)

---

解题思路

考虑这样一种情况

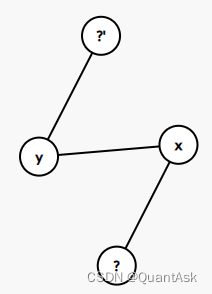
那么\(?\)和\(?'\)的交集恰好是\(x\)和\(y\)，也就是所有非叶子的连边我们都可以用以上方式确定。

然后考虑怎么确定叶子的连边，对于叶子\(x\)来说，包含它的集合中最小的那个肯定是它自己的集合。

这样我们就可以确定每个叶子对应的集合了，然后考虑怎么求它的父亲。

会发现我们如果把叶子的集合中的叶子去掉，那就只剩下它的父节点和它父节点连接的其他非叶子节点。

我们再处理出一个非叶子节点连边的集合，然后一个一个比较就可以找到这个点的父亲了。

然后要特判一些情况：

1. 没有非叶子节点：此时\(n=2\)直接特判。
2. 只有一个非叶子节点：此时随便找一个点都可以当非叶子节点。
3. 只有两个非叶子节点：此时叶子的集合分两种情况，分别对应不同的父节点就好了。

用\(bitset\)优化即可做到\(O(\frac{n^3}{\omega})\)

---

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<bitset>
#include<vector>
#define mp(x,y) make_pair(x,y)
using namespace std;
const int N=1050;
int n,k[N],f[N];;
bitset<N> b[N],g[N],c,v;
vector<pair<int,int> >e;
int main()
{
	scanf("%d",&n);
	for(int i=0;i<n;i++)f[i]=n,g[i][i]=1;k[n]=n+1;
	if(n==2)return puts("1 2")&0;
	for(int i=0;i<n;i++){
		scanf("%d",&k[i]);
		for(int j=1,x;j<=k[i];j++){
			scanf("%d",&x);x--;b[i][x]=1;
			f[x]=(k[i]<k[f[x]])?i:f[x];
		}
	}
	for(int i=0;i<n;i++)
		for(int j=i+1;j<n;j++){
			c=b[i]&b[j];
			if(c.count()==2){
				int a=c._Find_first();
				int b=c._Find_next(a);
				e.push_back(mp(min(a,b),max(a,b)));
				g[a][b]=g[b][a]=v[a]=v[b]=1;
			}
		}
	if(v.count()==0){
		for(int i=1;i<n;i++)
			printf("%d %d\n",i+1,1);
		return 0;
	}
	else if(v.count()==2){
		int p=v._Find_first();
		int q=v._Find_next(p);
		printf("%d %d\n",p+1,q+1);
		bool flag=0;
		for(int i=0;i<n;i++)
			if(!v[i]){
				if(flag){
					if(b[f[i]]==c)
						printf("%d %d\n",i+1,p+1);
					else printf("%d %d\n",i+1,q+1);
				}
				else printf("%d %d\n",i+1,p+1),c=b[f[i]],flag=1;
			}
		return 0;
	}
	for(int i=0;i<n;i++){
		if(v[i])continue;b[f[i]]&=v;
		for(int j=0;j<n;j++)
			if(b[f[i]]==g[j]){e.push_back(mp(min(i,j),max(i,j)));break;}
	}
	sort(e.begin(),e.end());
	for(int i=0;i<e.size();i++)
		if(!i||e[i]!=e[i-1])printf("%d %d\n",e[i].first+1,e[i].second+1);
	return 0;
}