[HDU7073] Integers Have Friends 2.0 -随机大法好

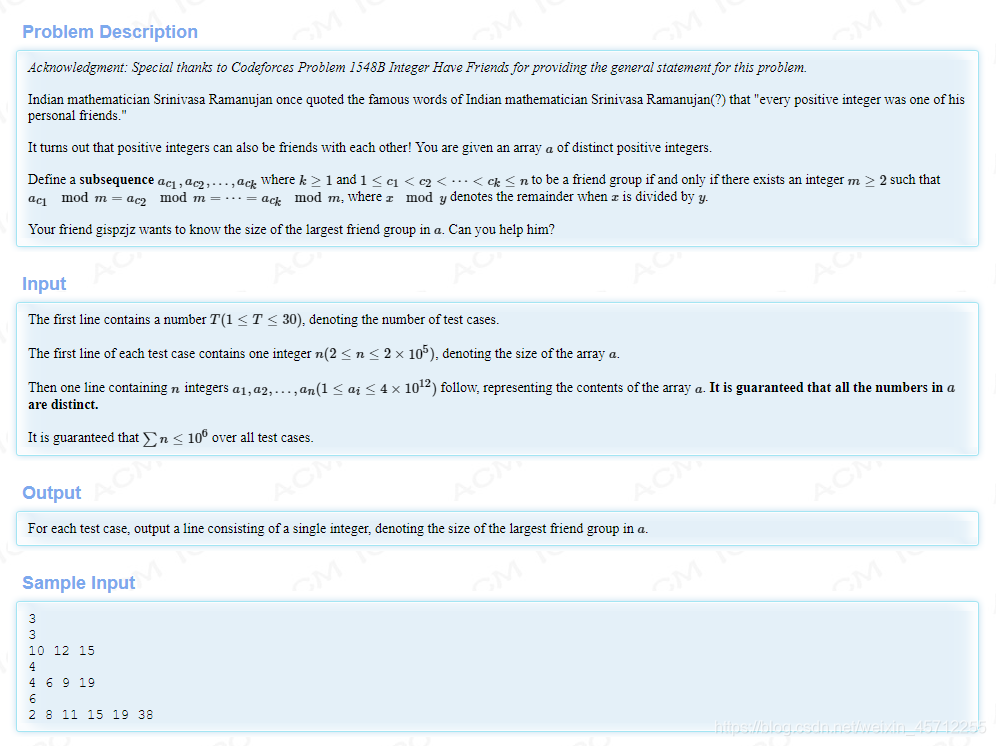
output

2
3
4

题意：
找到最大的一个集合，使得集合内所有元素 % m(>=2)
问最大的集合大小

对于第一组来讲：
可以选择m == 2 or 3
对于第二组来讲：
可以选择m == 5

在我们取m == 2的情况下，答案为 $\lceil \frac{n}{2}\rceil$

选择两个位置，这两个数的位置均在答案中的可能性至少为$\frac{1}{4}$，反之可能性为$\frac{3}{4}$，
假如重复取30次，则：

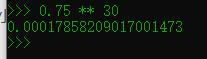
可以看作为0
所以方法是可靠的
选定了两个位置p1,p2之后，m可以取diff = abs(a[p1]-a[p2])的质因子
我们枚举diff的因子来当m进行操作，过程中一直取max即可

Code:

ll n,a[maxn];
ll cal(ll x,ll y) {
	ll ret = 0;
	for(int i=1; i<=n; i++) {
		if(a[i] % x == y) ret ++;
	}
	return ret;
}
int main() {
	srand(time(NULL));
	int _ = read;
	while(_ --) {
		n = read;
		for(int i=1; i<=n; i++) a[i] = read;
		ll ans = 1;
		for(int I = 1; I<=30; I++) {
			int p1 = rand() % n + 1;
			int p2 = rand() % n + 1;
			if(p1 == p2) continue;
			ll diff = abs(a[p1] - a[p2]);
			for(ll i=2; 1LL * i * i <= diff; i ++) {
				if(diff % i == 0) {
					while(diff % i == 0) diff /= i;
					ans = max(ans,cal(i,a[p1]%i));
				}
			}
			if(diff > 1) ans = max(ans,cal(diff,a[p1] % diff));
		}
		printf("%lld
",ans);
	}
	return 0;
}
/**
3
3
10 12 15
4
4 6 9 19
6
2 8 11 15 19 38

**/