『玩具装箱TOY 斜率优化DP』

<更新提示>

<第一次更新>

---

<正文>

玩具装箱TOY(HNOI2008)

Description

P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为 (1. . .N) 的 (N) 件玩具，第 (i) 件玩具经过压缩后变成一维长度为 (C_i)​ .为了方便整理，(P)教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第 (i) 件玩具到第 (j) 个玩具放到一个容器中，那么容器的长度将为 (x=j-i+sum_{k=i}^jC_k)​ 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 (x) ,其制作费用为 ((x-L)^2) .其中 (L) 是一个常量。(P)教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 (L) 。但他希望费用最小.

Input Format

第一行输入两个整数(N)，(L).接下来N行输入(C_i).(1<=N<=50000,1<=L,C_i<=10^7)

Output Format

输出最小费用

Sample Input

5 4
3
4
2
1
4

Sample Output

1

解析

简单分析题目大意：给定一个数列，可以将其分为若干个连续的子段，将区间([i,j])分为一段的花费为((j-i+sum_{k=i}^jC_k-L)^2)，求最小划分总花费。
由于没有需要划分多少段的限制，可以直接简单地设置状态：f[i]代表完成了前i个数的划分的最小花费和。
区间的花费是利用前缀和可以O(1)求解的，那么状态转移方程就是$$f_i=min{f_j+(i-(j+1)+sum_i-sum_j-L)^2}$$
暴力思路：(O(n^2))枚举(i,j)求解。
但是(50000)的数据(O(n^2))肯定不行啊，我们考虑优化这个dp。
先化简括号内花费内容：

[(i-(j+1)+sum_i-sum_j-L)^2 \=(i-j-1+sum_i-sum_j-L)^2 \=((i+sum_i)+(-L-1-j-sum_j))^2 \设a_k=(k+sum_k),b_k=(a_k+L+1) \=(a_i-b_j)^2 ]

代回原式：

[f_i=min{f_j+(a_i-b_j)^2} ]

假设我们已经找到了最优的(f_j)，那么：

[f_i=f_j+(a_i-b_j)^2 \⇒f_i=f_j+a_i^2-2a_ib_j+b_j^2 \⇒f_j+b_j^2=2a_ib_j+(f_i-a_i^2) ]

(将只与i有关的项和只与j有关的项分别整理)
这个时候我们发现式子中有一项是即和(i)有关有和(j)有关的，然后就可以做一些神奇的优化了。
我们视(f_j+b_j^2)为(y)，(b_j)为(x)，(2a_i)为(k)，((f_i+a_i^2))为(b)，那么我们就可以把它当做一个一次函数的的表达式(y=kx+b)。而且这个一次函数需满足：

1.过定点((b_j,f_j+b_j^2))，由于这个点只和(j)有关，称其为(P_j)
2.其斜率为(2a_i)

这时候，我们需要重新定义(f_i)的含义：满足两个要求的一次函数的截距((b))加上(a_i^2)。
由于(a_i^2)的值是确定的，我们需要求最小的(f_i)，即求做小的一次函数的截距。
我们将满足斜率为(2a_i)的直线以及点(P_1,P_2,...,P_j)描述在图中:

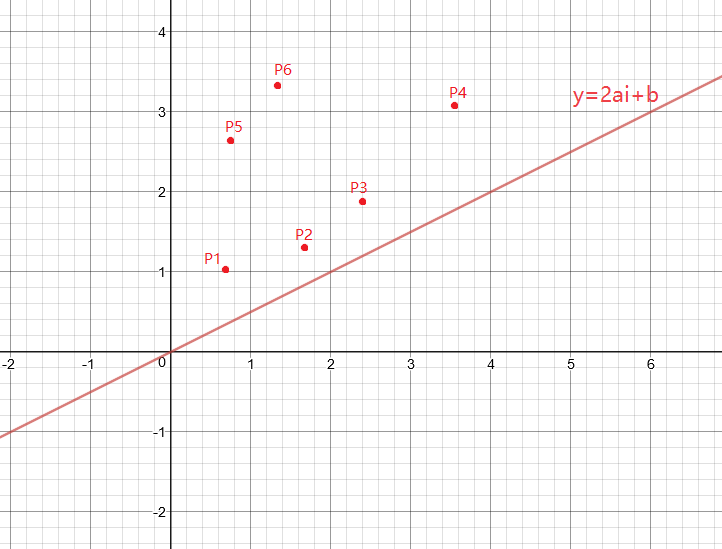
直线自下向上移动，只要它过任何一个点(P)，它就成为了符合要求的直线。
我们要求截距最小，显然，当它自下向上移动过的第一个点(P_j)时，截距最小。如图，此时能取得截距最小的点是(P_2)。那么由上可知，(j=2)时，一次函数的截距最小，更新得到的(f_i)也是最小的。
所以，我们的目标就转变为了找到一次函数能够第一个“碰到”的点。

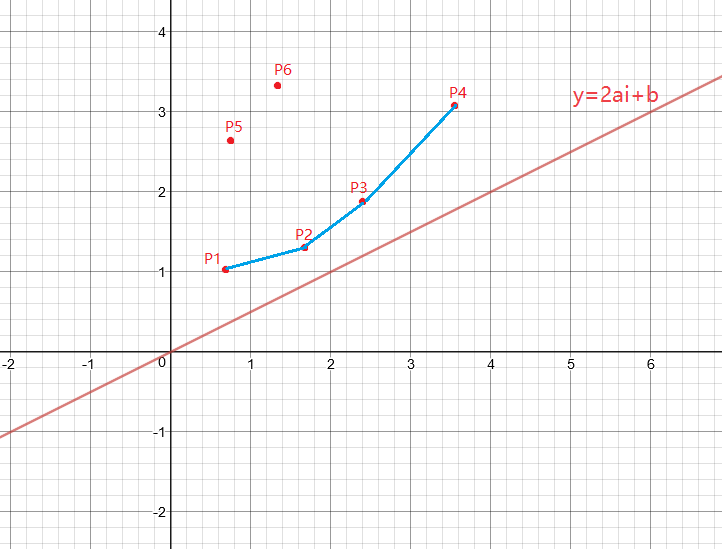
观察上图，我们将最有可能与直线先“碰到”的点(最外围的点)两两相连，发现：它们近似的构成了一个下凸壳的形状，两两相连的线段所在的直线的斜率依次递增。
此时我们发现了一个很好的性质，我们的目标直线第一个过的点最优点(P_j)满足：(P_j,P_{j+1})所在直线是斜率大于目标直线斜率的第一条直线。((P_2,P_3)构成的直线的斜率大于图中直线的斜率，但(P_1,P_2)构成的直线的斜率小于图中直线的斜率，所以(P_2)为最优点)

那么这就成为了我们的突破口了：由于构成下凸壳直线满足斜率单调递增，我们用单调队列维护这些(P)点。由于随着i的增加，(a_i)也是单调递增的，这就应和了单调队列的操作。
对于每一个(i)，我们让斜率小于(2a_i)的单调队列中的直线所对应的点出队(它小于当前的(2a_i)，由于(a_i)单调递增，它也一定小于以后的(2a_i)，所以这些点将会是一直无用的，可以直接出队)，直到找到第一条斜率大于(2a_i)的直线，此时，队头的点的编号j即为最优决策。我们直接利用该决策转移。
完成转移以后，新的点(P_i)也需要加入队列里，此时，我们还要维护一个操作：

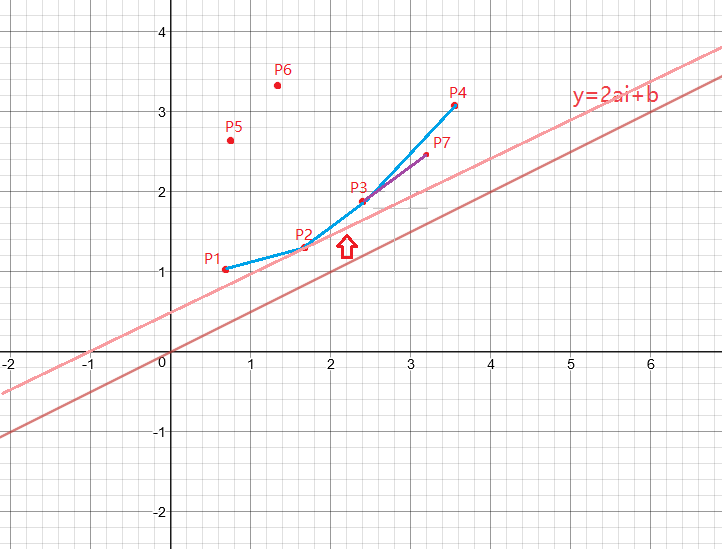
当(P_i)(图中的(P_7))加入后，我们发现，原来的(P_4,P_3)构成的直线的斜率大于(P_3)和新的(P_4)构成的斜率，这样，(P_4)就到了内部，新的下凸壳由(P_1,P_2,P_3,P_7)构成，我们需要让(P_4)出队。
即当(slope(q[tail],q[tail-1])>slope(q[tail-1],i))((slope)代表斜率函数)时，队尾出队。

事实上，我们在不断维护一个下凸壳的形状，由于单调队列一共会进出至多N个点，所以，这样实现转移的时间复杂度是(O(n))的，我们将此种优化方法称为斜率优化。

(Code:)

#include<bits/stdc++.h>
using namespace std;
const int N=50000+80;
long long f[N],q[N],sum[N],toy[N],n,L,head,tail;
inline long long a(long long k){return sum[k]+k;}
inline long long b(long long k){return a(k)+L+1;}
inline long long x(long long k){return b(k);}
inline long long y(long long k){return f[k]+b(k)*b(k);}
inline double slope(long long p,long long q){return ((y(p)-y(q))*1.0)/((x(p)-x(q))*1.0);}
int main(void)
{
	freopen("toy.in","r",stdin);
	freopen("toy.out","w",stdout);
	scanf("%lld%lld",&n,&L);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&toy[i]);
		sum[i]=sum[i-1]+toy[i];
	}
	for(int i=1;i<=n;i++)
	{
		while(head<tail&&slope(q[head],q[head+1])<2*a(i))head++;
		f[i]=f[q[head]]+(a(i)-b(q[head]))*(a(i)-b(q[head]));
		while(head<tail&&slope(q[tail],q[tail-1])>slope(q[tail-1],i))tail--;
		q[++tail]=i;
	}
	printf("%lld
",f[n]);
}

---

<后记>