单调栈原理与单调队列类似,就是队列与栈的差别.(感觉单调队列的应用比单调栈更广)
如图所示,在一条水平线上有n个宽为1的矩形,求包含于这些矩形的最大子矩形面积(图中的阴影部分的面积即所求答案)。
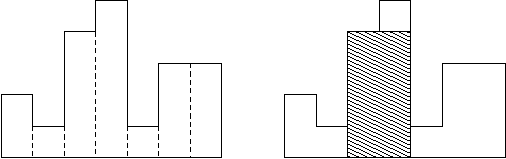
根据单调队列的思想,建立一个栈,用来保存若干个矩形,这些矩形的高度是单调递增的.从左到右依次扫描每个矩形:
1 如果当前矩形比栈顶矩形高,直接进栈
2 否则,不断把栈内比当前矩形高的的矩形出栈,直到栈为空或者栈顶矩形的高度比当前矩形小.在出栈过程中,累计被弹出的矩形的宽度之和,并且每弹出一个矩形,就用该矩形的高度乘上以经累计的宽度去更新答案max.整个出栈过程结束后,把高度为当前扫描到的矩形高度,宽度为累计宽度的新矩形入栈.
3 整个扫描结束后,还要计算栈内剩余矩形能够构成的最大矩形面积,方法跟步骤2类似.
第2步看文字不理解的话,建议手画几个高矮不齐的矩形根据代码模拟一下,一定要弄懂,这是单调栈的核心思想.
while(~scanf("%d",&n)){
if(!n)break;
int top=0;
//模拟栈顶指针
long long ans=0;
//记录最大面积ans
for(int i=1;i<=n;i++)h[i]=read();
//读入每个矩形的高度
h[n+1]=0;
//这是一个为了实现第3步的小技巧
for(int i=1;i<=n+1;i++){
if(h[i]>=st[top]){
top++;
st[top]=h[i];
wid[top]=1;
}
//如果当前扫描到的矩形的高度比栈顶矩形高度大
//直接把当前矩形入栈,同时该矩形宽度设为1
else{
int width=0;
while(st[top]>h[i]){
width+=wid[top];
//累计出栈矩形高度
ans=max(ans,(long long)width*st[top]);
//同时把该出栈矩形的高度乘累计宽度以更新最大值
top--;
}
st[++top]=h[i];
wid[top]=width+1;
//把高度为当前扫描到的矩形的高度
//宽度为累计宽度的新矩形入栈
}
}
printf("%lld
",ans);
}