知道是数独问题后犹豫了一下要不要做(好像很难的样纸==。),用dfs并剪枝,是一道挺规范的搜索题。
先介绍以下数独吧~
数独(Sudoku)是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格 的数字,并满足每一行、每一列、每一个粗线宫内的数字均含1-9,不重复。 每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
有一种求解数独问题的方案是“候选数字法”,就是在待填充的格子中填写不会造成行重复、列重复、块重复的数字,有的时候存在多个这样的数字,那么我们可以随机选取一个,如果待填充的格子中填写任何一个数字都会造成某种重复的发生,则说明这个问题没有解,也就是这不是一个数独问题。
想要更加深入了解的同学可以点此链接:http://www.cnblogs.com/grenet/archive/2013/06/19/3138654.html
下面来说说POJ的这道题吧!
题目大意:
给你一个数独,让你填数:
1.每行的九个数字互不相同;
2.每列的九个数字各不相同;
3.被分成的3*3的小矩阵中的九个数字互不相同;
输出完成后的数表,若不能满足上述条件,则输出原图。
解题思路:
DFS。。失败了回溯~
从小优女神那里看到的存储方式(觉得很是方便呀!)
用三个数组进行标记每行、每列、每个子网格已用的数字,用于剪枝
bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了
bool small[10][10]; //small[k][x] 标记在第k个3*3子格中数字z是否出现了
row 和 col的标记比较好处理,关键是找出small子网格的序号与 行i列j的关系
即要知道第i行j列的数字是属于哪个子网格的
首先我们假设子网格的序号如下编排:
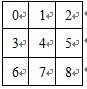
由于1<=i、j<=9,我们有: (其中“/”是C++中对整数的除法)
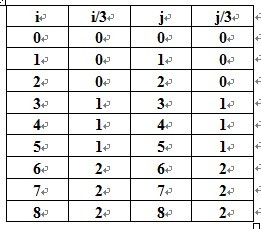
令a= i/3 , b= j/3 ,根据九宫格的 行列 与 子网格 的 关系,我们有:
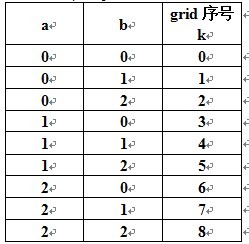
不难发现 3a+b=k
即 3*(i/3)+j/3=k
又我在程序中使用的数组下标为 1~9,grid编号也为1~9
因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k
这样我们就能记录k个3*3子格中数字z是否出现了:
下面是我的代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cstring> 5 #include<cmath> 6 #include<algorithm> 7 #include<cstdlib> 8 #include<vector> 9 #define inf 1<<25 10 #define LL long long 11 using namespace std; 12 int row[10][10]; 13 int col[10][10]; 14 int map[10][10]; 15 int small[10][10]; 16 int f(int x,int y) 17 { 18 return 3*((x-1)/3)+(y-1)/3+1; 19 } 20 void init() 21 { 22 int i,j; 23 char ch; 24 memset(row,0,sizeof(row)); 25 memset(col,0,sizeof(col)); 26 memset(small,0,sizeof(small)); 27 for(i=1; i<=9; i++) 28 { 29 for(j=1; j<=9; j++) 30 { 31 scanf("%c",&ch); 32 map[i][j]=ch-'0'; 33 if(map[i][j]) 34 { 35 int k; 36 k=f(i,j); 37 row[i][map[i][j]]=1; 38 col[j][map[i][j]]=1; 39 small[k][map[i][j]]=1; 40 } 41 } 42 getchar(); 43 } 44 } 45 int dfs(int x,int y) 46 { 47 if(x==10) 48 return 1; 49 int flag=0; 50 if(map[x][y]) 51 { 52 if(y==9) 53 flag=dfs(x+1,1); 54 else 55 flag=dfs(x,y+1); 56 if(flag) 57 return 1; 58 else 59 return 0; 60 } 61 else 62 { 63 int k=f(x,y); 64 for(int i=1; i<=9; i++) 65 if(!row[x][i] && !col[y][i] && !small[k][i]) 66 { 67 map[x][y]=i; 68 row[x][i]=1; 69 col[y][i]=1; 70 small[k][i]=1; 71 if(y==9) 72 flag=dfs(x+1,1); 73 else 74 flag=dfs(x,y+1); 75 if(!flag) 76 { 77 map[x][y]=0; 78 row[x][i]=0; 79 col[y][i]=0; 80 small[k][i]=0; 81 } 82 else 83 return 1; 84 } 85 } 86 return 0; 87 } 88 int main() 89 { 90 int t; 91 scanf("%d",&t); 92 getchar(); 93 while(t--) 94 { 95 init(); 96 dfs(1,1); 97 for(int i=1; i<=9; i++) 98 { 99 for(int j=1; j<=9; j++) 100 printf("%d",map[i][j]); 101 printf(" "); 102 } 103 } 104 return 0; 105 }