linprog 四要素:
[minquad c^Tx
]
[s.t.quad
egin{cases}
Acdot xleq b\
Aeqcdot x=beq\
lbleq xleq ub
end{cases}
]
其中, c 和 x 为 n 维向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。
Matlab 中求解线性规划的命令为以下几种:
x=linprog(c,A,b)
x=linprog(c,A,b,Aeq,beq)
x=linprog(c,A,b,Aeq,beq,lb,ub) % 最常用的一种形式
x=linprog(c,A,b,Aeq,beq,lb,ub,x0)
x=linprog(c,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval]=linprog(…)
[x, fval, exitflag]=linprog(…)
[x, fval, exitflag, output]=linprog(…)
[x, fval, exitflag, output, lambda]=linprog(…)
其中 x 返回的是决策向量的取值,favl 返回的是目标函数的最优值, c 为价值向量,A,b对应的是 线性不等式约束,Aeq,beq对应的是 线性等式约束,lb 和 ub 分别对应的是 决策向量的下界向量与上界向量。
例子:
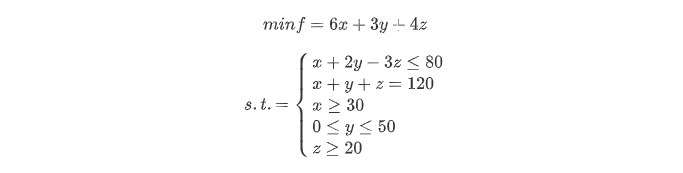
代码:
clear;
clc;
c=[6 3 4];
A=[1 2 -3;0 1 0];
b=[80;50];
Aeq=[1 1 1];
beq=[120];
lb=[30 0 20];
ub=[];
[x,favl]=linprog(c,A,b,Aeq,beq,lb,ub)
结果展示:
Optimal solution found.
x =
30.0000
50.0000
40.0000
favl =
490
>>