主讲人 网络上的尼采
(新浪微博: @Nietzsche_复杂网络机器学习)
网络上的尼采(813394698) 9:05:00
今天的主要内容:Markov Chain Monte Carlo,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hybrid Monte Carlo。
上一章讲到的平均场是统计物理学中常用的一种思想,将无法处理的复杂多体问题分解成可以处理的单体问题来近似,变分推断便是在平均场的假设约束下求泛函L(Q)极值的最优化问题,好处在于求解过程中可以推出精致的解析解。变分是从最优化的角度通过坐标上升法收敛到局部最优,这一章我们将通过计算从动力学角度见证Markov Chain Monte Carlo收敛到平稳分布。
先说sampling的原因,因为统计学中经常会遇到对复杂的分布做加和与积分,这往往是intractable的。MCMC方法出现后贝叶斯方法才得以发展,因为在那之前对不可观测变量(包括隐变量和参数)后验分布积分非常困难,对于这个问题上一章变分用的解决办法是通过最优化方法寻找一个和不可观测变量后验分布p(Z|X)近似的分布,这一章我们看下sampling的解决方法,举个简单的例子:比如我们遇到这种形式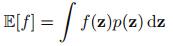 ,z是个连续随机变量,p(z)是它的分布,我们求f(z)的期望。如果我们从p(z)中sampling一个数据集z(l),然后再求个平均
,z是个连续随机变量,p(z)是它的分布,我们求f(z)的期望。如果我们从p(z)中sampling一个数据集z(l),然后再求个平均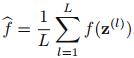 来近似f(z)的期望,so,问题就解决了,关键是如何从p(z)中做无偏的sampling。
来近似f(z)的期望,so,问题就解决了,关键是如何从p(z)中做无偏的sampling。
为了说明sampling的作用,我们先举个EM的例子,最大似然计算中求分布的积分问题,我们在第九章提到了,完整数据的log似然函数是对隐变量Z的积分:
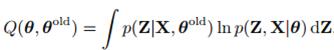
如果Z是比较复杂的分布,我们就需要对Z进行采样,从而得到:
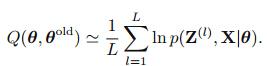
具体就是从Z的后验分布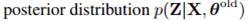 中进行采样。
中进行采样。
如果我们从贝叶斯的观点,把EM参数theta也当成一个分布的话,有下面一个IP算法:

I步,我们无法直接对P(Z|X)取样,我们可以先对P(theta|X)取样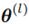 ,然后再对Z的后验分布进行取样:
,然后再对Z的后验分布进行取样: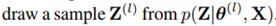
P步,利用上一步对P(Z|X)的取样,来确定新的参数分布:
然后按这个I步和P步的方式迭代。
接下来我们讲sampling methods,为了节省时间,两个基本的rejection sampling和Importance sampling不讲了,这两种方法在高维下都会失效,我们直奔主题MCMC(Markov Chain Monte Carlo )。蒙特卡洛,是个地中海海滨城市,气候宜人,欧洲富人们的聚集地,更重要的是它是世界三大赌城之一,用这个命名就知道这种方法是基于随机的,过会我们会讲到。马尔科夫大神就不用多说了,他当时用自己的名字命名马尔科夫链是预见到这个模型巨大作用。他还有一个师弟叫李雅普洛夫,控制论里面的李雅普洛夫函数说的就是这位,他们的老师叫契比雪夫,都是圣彼得堡学派的。俄国数学家对人类的贡献是无价的orz
最早的MCMC方法是美国科学家在研制原子弹时算积分发明的。我们先介绍一个最基本的Metropolis方法,这种方法的接受率是:
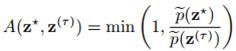
但有个要求,就是proposal distribution满足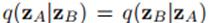 。过程很简单,我们先找个比较容易采样的分布即proposal分布,然后从这个分布中取一个样本Z*,如果
。过程很简单,我们先找个比较容易采样的分布即proposal分布,然后从这个分布中取一个样本Z*,如果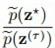 大于1直接接受,如果小于1就接着算出接受率,并且从(0,1)之间取一个随机数和这个接受率做比较来决定是否接受这个样本。过会会在Metropolis-Hastings algorithm方法中具体说。下图是一个简单的例子,对高斯分布做采样,绿线是表示接受的步骤,红线表示拒绝的:
大于1直接接受,如果小于1就接着算出接受率,并且从(0,1)之间取一个随机数和这个接受率做比较来决定是否接受这个样本。过会会在Metropolis-Hastings algorithm方法中具体说。下图是一个简单的例子,对高斯分布做采样,绿线是表示接受的步骤,红线表示拒绝的:

讲Metropolis-Hastings方法前,我们先来回顾下马尔科夫链的性质,这个很重要。markov chains最基本的性质就是无后效性,就是这条链的下一个节点的状态由当前节点状态完全决定:
特定的齐次马尔科夫链可以收敛到平稳分布,也就是经过相当长的一段时间转移,收敛到的分布和初始值无关,转移核起着决定的作用。关于马尔科夫链的收敛,我们将介绍一个充分条件:detailed balance细致平稳条件。
先介绍两个公式,马尔科夫链节点状态的marginal distribution计算公式,由于无后效性我们可以得到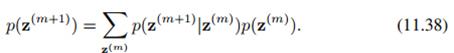
上面公式的加和结合马儿科夫链的状态转移矩阵是比较容易理解。
平稳分布的定义就是下面的形式:
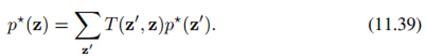
其中 是z'到z的转移概率,上面的公式不难理解,就是转移后分布不再发生变化。
是z'到z的转移概率,上面的公式不难理解,就是转移后分布不再发生变化。
下面我们给出细致平稳条件的公式: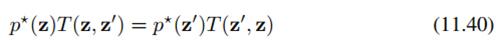
满足细致平稳条件就能收敛到平稳分布,下面是推导: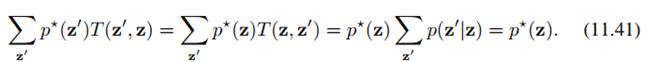
我们把上面细致平稳条件的公式11.40代入公式11.41最左边,从左朝右推导就是平稳分布的公式11.39。细致平稳条件的好处,就是我们能控制马尔科夫链收敛到我们指定的分布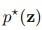 。以后的Metropolis-Hastings方法及改进都是基于这个基础的。
。以后的Metropolis-Hastings方法及改进都是基于这个基础的。
前面我们提到,Metropolis方法需要先选一个比较容易取样的proposal distribution,从这个分布里取样,然后通过接受率决定是否采用这个样本。一个简单的例子就是对于proposal distribution我们可以采用Gaussian centred on the current state,其实很好理解,就是上一步节点的值可以做下一步节点需要采样的proposal distribution即高斯分布的均值,这样下一步节点的状态由上一步完全决定,这就是一个马尔科夫链。马尔科夫链有了,我们怎么保证能收敛到目标分布呢?就是前面说的细致平稳条件,我们可以通过设置接受率的形式来满足这个条件。Metropolis-Hastings接受率的形式:

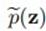 来自于
来自于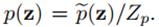 ,分布q便是proposal distribution。
,分布q便是proposal distribution。
范涛@推荐系统(289765648) 10:49:15
Zp 是什么?
网络上的尼采(813394698) 10:52:04
Zp是分布中和z无关的部分。
为了使各位有个形象的理解,我描述一下过程,我们把 当做高斯分布的均值,方差是固定的。然后从这个分布取一个样本就是
当做高斯分布的均值,方差是固定的。然后从这个分布取一个样本就是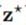 ,如果
,如果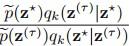 大于1肯定接受,如果小于1,我们便从(0,1)之间取一个随机数,和这个接受率做比较,如果接受率大于这个随机数便接受,反之便拒绝。接受率这么设就能满足细致平稳条件的原因,看这个(11.45)公式:
大于1肯定接受,如果小于1,我们便从(0,1)之间取一个随机数,和这个接受率做比较,如果接受率大于这个随机数便接受,反之便拒绝。接受率这么设就能满足细致平稳条件的原因,看这个(11.45)公式: 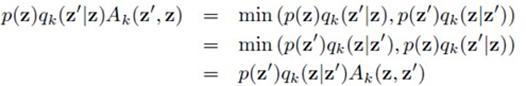

我们把接受率公式11.44代入上面的公式的左边,会推出左右两边就是细致平稳条件的形式,红框部分便是细致平稳条件公式11.40的转移核,书上的公式明显错了,上面的这个是勘误过的。
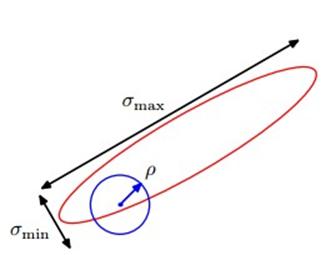
刚才说了proposal distribution一般采用Gaussian centred on the current state,高斯分布的方差是固定的,其实方差就是步长,如何选择步长这是一个state of the art问题,步子太小扩散太慢,步子太大,拒绝率会很高,原地踏步。书中的一个例子,当用Gaussian centred on the current state作proposal distribution时,步长设为目标高斯分布的最小标准差最合适:
下面讲Gibbs Sampling,Gibbs Sampling其实是每次只对一个维度的变量进行采样,固定住其他维度的变量,然后迭代,可以看做是Metropolis-Hastings的特例,它的接受率一直是1.
步骤是比较容易理解的,跟上一章的变分法的有相似之处。假设有三个变量的分布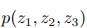 ,
,
先固定住z2 z3对z1进行采样,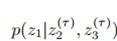 ;
;
然后固定住z1 z3对z2进行采样,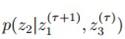 ;
;
然后是Z3,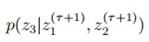
如此迭代。
根据Metropolis-Hastings,它的接受率恒为1。看下面的推导:
因为其他维度是固定不变的,所以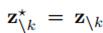 ,代入上式就都约去了,等于1.
,代入上式就都约去了,等于1.
最后对于图模型采用gibbs sampling,条件概率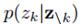 可以根据马尔科夫毯获得,下面一个是无向图,一个是有向图,蓝色的节点是和要采样的变量有关的其他变量:
可以根据马尔科夫毯获得,下面一个是无向图,一个是有向图,蓝色的节点是和要采样的变量有关的其他变量:
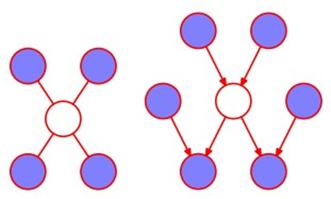
关于更多的gibbs sampling的内容可以看MLAPP,里面有blocked gibbs和collapsed gibbs。
刚才提到Metropolis-Hastings对步长敏感,针对这个问题,下面介绍两个增加辅助变量的方法,这些方法也是满足细致平稳条件的。先介绍slice sampling,这种方法增加了一个变量U,可以根据分布的特征自动调整步长: 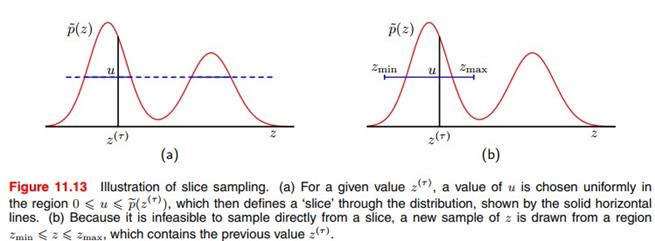
步骤很简单:在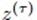 与
与 之间的这段距离随机取个值U,然后通过U画个横线,然后在包含
之间的这段距离随机取个值U,然后通过U画个横线,然后在包含 并且
并且 这段横线对z进行随机采样,然后按这种方式迭代。图(b)为了实际中便于操作,有时还需要多出那么一段,因为我们事先不知道目标分布的具体形式,所以包含
这段横线对z进行随机采样,然后按这种方式迭代。图(b)为了实际中便于操作,有时还需要多出那么一段,因为我们事先不知道目标分布的具体形式,所以包含 并且
并且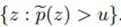 这段横线没法确定,只能朝外延伸加单位长度进行试,最后会多出来一段,这一点书上并没有介绍详细。
这段横线没法确定,只能朝外延伸加单位长度进行试,最后会多出来一段,这一点书上并没有介绍详细。
下面介绍The Hybrid Monte Carlo Algorithm (Hamiltonian MCMC):哈密顿,神童,经典力学三巨头之一,这个算法引入了哈密顿动力系统的概念,计算接受率时考虑的是系统的总能量。Hybrid Monte Carlo 定义了势能和动能两种能量,它们的和便是系统总能量哈密顿量。先看势能,分布可以写成这种形式:
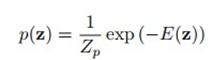
E(z)便是系统的势能。
另外增加一个变量,状态变量变化的速率: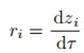
系统的动能便是:
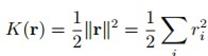
总的能量便是: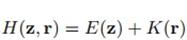
比如高斯分布的哈密顿量就可表示为:
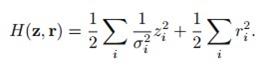
下面这个公式便是Hybrid Monte Carlo 的接受率:

可以证明 这种接受率是满足detailed balance条件的。
ORC(267270520) 12:14:03
推荐一本相关的书 Introducing Monte Carlo Methods with R (use R) ,PS:R做MCMC很方便。
赞尼采讲的很精彩,学习了,嘿嘿
网络上的尼采(813394698) 12:36:37
Markov Chain Monte Carlo In Practice(Gilks)这本书也挺不错。
红烧鱼(403774317) 12:38:06
这本读研的时候生读过,非常实用,随书附带code
网络上的尼采(813394698)
最后需要补充的是:判断MCMC的burn-in何时收敛是个问题,koller介绍了两种方法,即同一条链上设置不同的时间窗做比较,另一种同时跑多条链然后作比较。当然也有一条链跑到黑的。
PRML读书会讲稿PDF版本以及更多资源下载地址:http://vdisk.weibo.com/u/1841149974