@(162 - 信号处理)
整理转载自:给小白图示讲解OFDM
下面以图示为主讲解OFDM,以"易懂"为第一要义。
注:下面的讨论如果不做说明,均假设为理想信道。
一张原理图

章节一:时域上的OFDM——子载波正交的原理
OFDM的"O"代表着"正交",那么就先说说正交吧。
首先说说最简单的情况,sin(t)和sin(2t)是正交的【证明:sin(t)·sin(2t)在区间[0,2π]上的积分为0】,而正弦函数又是波的最直观描述,因此我们就以此作为介入点。既然本文说的是图示,那么我们就用图形的方式来先理解一下正交性。【你如果能从向量空间的角度,高屋建瓴的看待这个问题的话,你也就不是"小白"了,R U?】
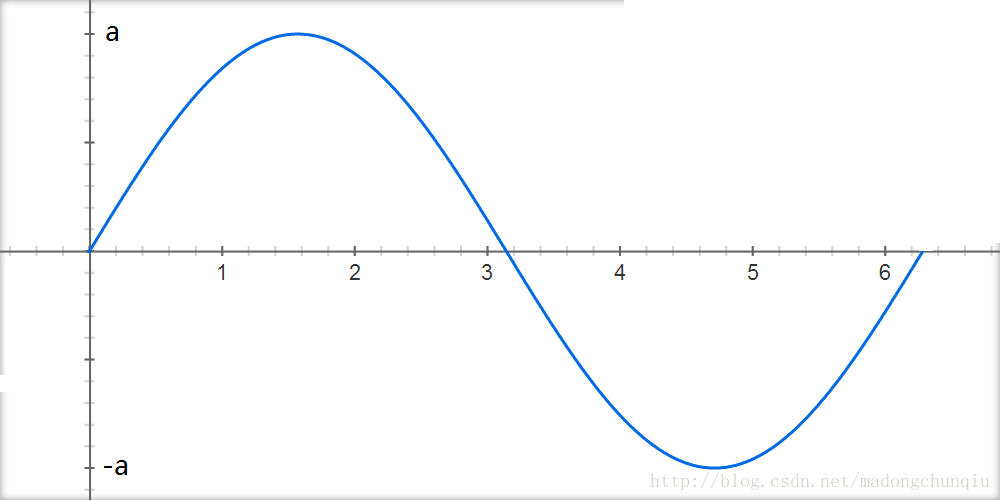
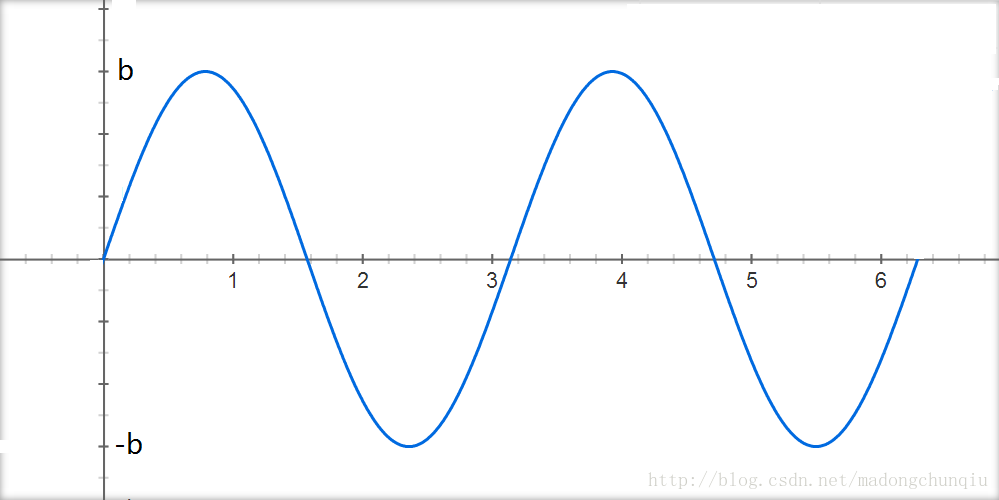
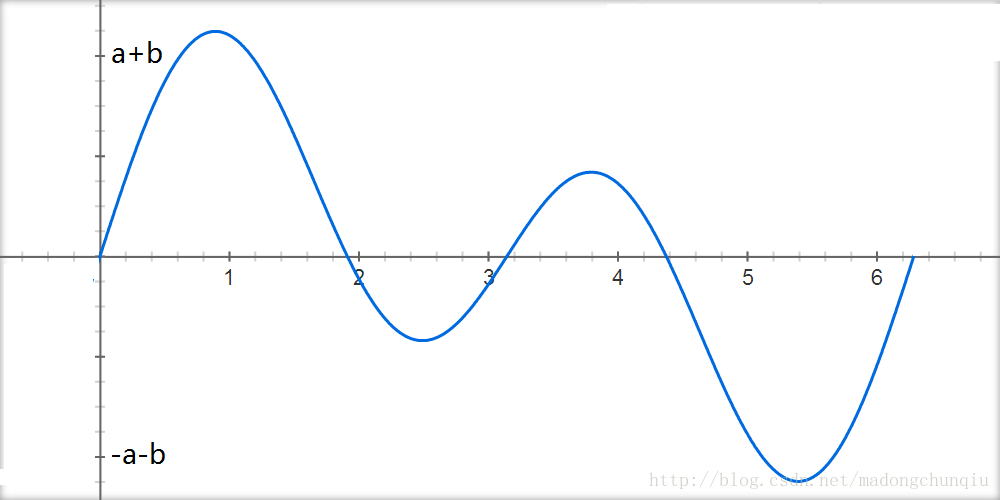
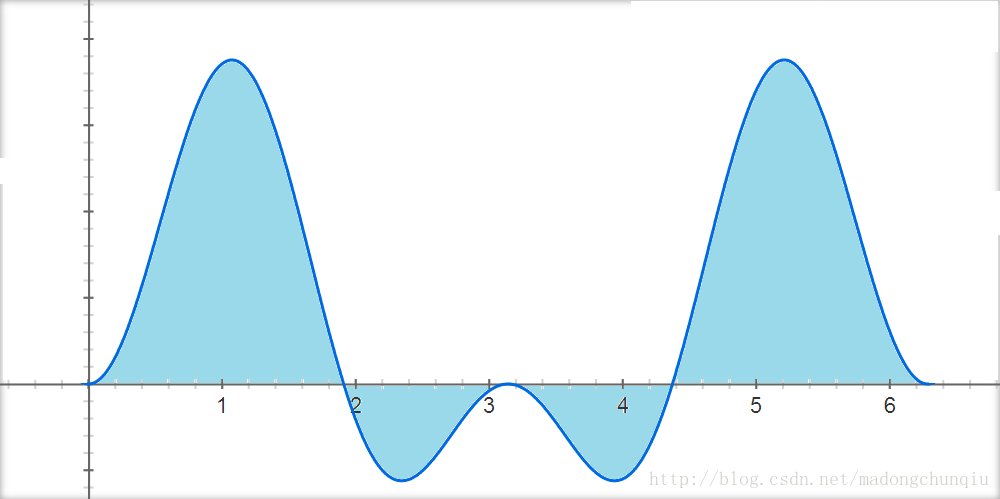
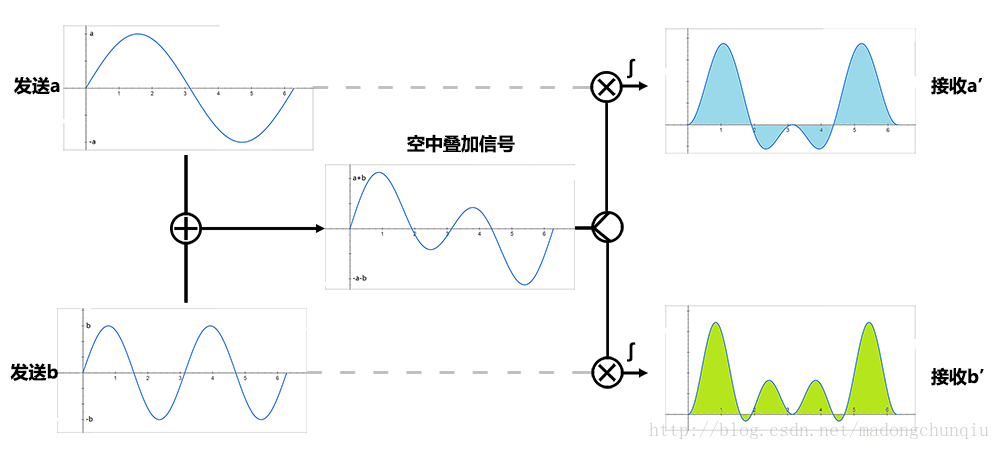
在下面的图示中,在[0,2π]的时长内,采用最易懂的幅度调制方式传送信号:sin(t)传送信号a,因此发送a·sin(t),sin(2t)传送信号b,因此发送b·sin(2t)。其中,sin(t)和sin(2t)的用处是用来承载信号,是收发端预先规定好的信息,在本文中一律称为子载波;调制在子载波上的幅度信号a和b,才是需要发送的信息。因此在信道中传送的信号为a·sin(t)+b·sin(2t)。在接收端,分别对接收到的信号作关于sin(t)和sin(2t)的积分检测,就可以得到a和b了。(以下图形采用google绘制)
图一:发送a信号的sin(t)
图二:发送b信号的sin(2t)【注意:在区间[0,2π]内发送了两个完整波形】
图三:发送在无线空间的叠加信号a·sin(t)+b·sin(2t)
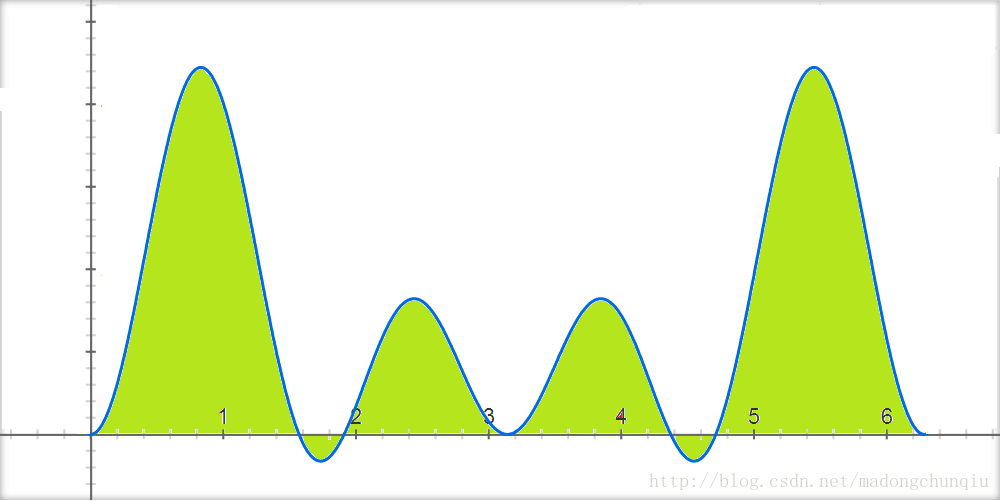
图四:接收信号乘sin(t),积分解码出a信号。【如前文所述,传送b信号的sin(2t)项,在积分后为0】
图五:接收信号乘sin(2t),积分解码出b信号。【如前文所述,传送a信号的sin(t)项,在积分后为0】
图六:流程图
到了这里,也许你会出现两种状态:
一种是:啊,原来是这样,我懂了。
一种是:啊,怎么会这样,我完全无法想象。这里要说的是,你根本用不着去想象(visualize)。
数学中是如此定义正交的,数学证明了它们的正交性,那么他们就是正交的,【他们就可以互不干扰的承载各自的信息】。选取sin(t)和sin(2t)作为例子,正是因为它们是介于直观和抽象的过渡地带,趟过去吧。
上面的图示虽然简单,但是却是所有复杂的基础。
1.1 下一步,将sin(t)和sin(2t)扩展到更多的子载波序列({sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),...,sin(2π·Δf·kt)}) (例如k=16,256,1024等),应该是很好理解的事情。
其中,(2π)是常量;(Δf)是事先选好的载频间隔,也是常量。(1t,2t,3t,...,kt)保证了正弦波序列的正交性。
1.2 再下一步,将cos(t)也引入。容易证明,cos(t)与sin(t)是正交的,也与整个sin(kt)的正交族相正交。同样,cos(kt)也与整个sin(kt)的正交族相正交。因此发射序列扩展到({sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),...,sin(2π·Δf·kt),cos(2π·Δf·t),cos(2π·Δf·2t),cos(2π·Δf·3t),...,cos(2π·Δf·kt)})也就顺理成章了。
1.3 经过前两步的扩充,选好了2组正交序列sin(kt)和cos(kt),这只是传输的"介质"。真正要传输的信息还需要调制在这些载波上,即sin(t),sin(2t),...,sin(kt)分别幅度调制a1,a2,...,ak信号,cos(t),cos(2t),...,cos(kt)分别幅度调制b1,b2,...,bk信号。这2n组互相正交的信号同时发送出去,在空间上会叠加出怎样的波形呢?做简单的加法如下:$$f(t) = a1·sin(2π·Δf·t) +
a2·sin(2π·Δf·2t) +
a3·sin(2π·Δf·3t) +
...
ak·sin(2π·Δf·kt) +
b1·cos(2π·Δf·t) +
b2·cos(2π·Δf·2t) +
b3·cos(2π·Δf·3t) +
...
bk·cos(2π·Δf·kt) +
= ∑ak·sin(2π·Δf·kt) + ∑bk·cos(2π·Δf·kt) $$【公式1-1:实数的表达】为了方便进行数学处理,上式有复数表达形式如下:
(f(t) = ∑Fk·e^{j·2π·Δf·kt}) 【公式1-2:复数的表达】
上面的公式可以这样看:每个子载波序列都在发送自己的信号,互相交叠在空中,最终在接收端看到的信号就是f(t)。接收端收到杂糅信号f(t)后,再在每个子载波上分别作相乘后积分的操作,就可以取出每个子载波分别承载的信号了。
然后,多看看公式1-1和公式1-2!!!发现咯?这就是傅里叶级数嘛。
如果将t离散化,那么就是离散傅立叶变换。所以才有OFDM以FFT来实现的故事。将在下面的章节进行更多的描述。
遵循古老的传统,F表示频域,f表示时域,所以可以从公式1-2中看出,每个子载波上面调制的幅度,就是频域信息。类似的说法是:OFDM传输的是频域信号。这种说法有些别扭,但是很多教程或文章会使用这样的说明方式,就看读者如何理解了。如果纯粹从公式或者子载波来看,这种说法其实也是很直接的阐述了。
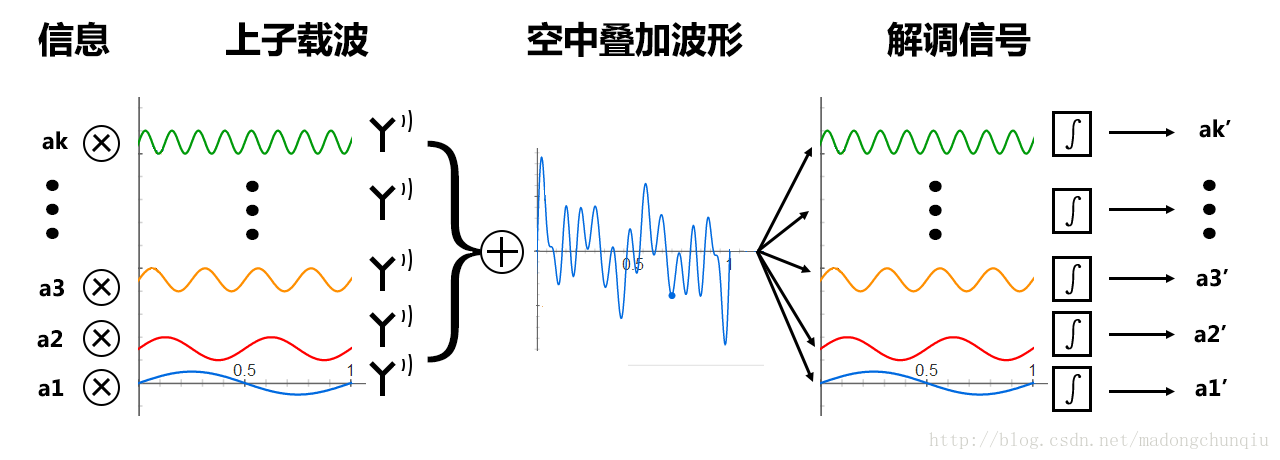
上面1.1-1.3的扩展,可如下图所示:
图七:时域上的OFDM系统图
1.4 还有这一步吗?其实是有的。"小白"你可以先想想,想不到的话先往下看,因为这需要在频域中考量,所以我写在后面了。【也可参考[1]】
将上述的时域分析配上LTE的实现,有如下情况:
【注1:本段描述需要有LTE物理层的基本知识,如果看不明白,请暂时跳过,看完整篇文章后再回看】
【注2:LTE并非时域的实现,下面仅仅是套用LTE的参数,做一个参考分析】
子载波的间隔Δf=15kHz,一个OFDM symbol的发送时间是66.7us,可以发现,15kHz*66.67us=1,即基带上一个OFDM symbol的发送时间正好发送一个一次谐波的完整波形。对于10M的LTE系统,采用的是1024个子载波,但是只有中间600个(不含最中间的直流)子载波被用于传送数据。在一个OFDM symbol的时间内(即66.67us),靠近中间的两个一次谐波传输一个完整波形,再靠外一点的两个二次谐波传输两个完整波形,以此类推至最外面的两个300次谐波传输了300个完整的波形。在这66.67us内,600个子载波互相正交,其上分别承载了600个复数信号。
上面的说法有点啰嗦,不如图示来得直观。本来准备再画一图的,不过一来上面已经有了类似的图,实是大同小异;二来,600个子载波,也太多了点。。。
OK,说到这里,从时域上面来看OFDM,其实是相当简洁明快讨人喜欢的。不过,一个系统若要从时域上来实现OFDM,难度太大,时延和频偏都会严重破坏子载波的正交性,从而影响系统性能。这点在各种教材文章中都会有提及,我就不赘述了。
下面将转入频域来描述OFDM,由于频域不甚直观,的确会稍稍让人费解。不过只要时刻想着时域子载波间的叠加,一切都会好起来。
章节二:频域上的OFDM——子载波正交后,达到理想频带利用率
第一章节时域上的讨论开始于OFDM中的"O";本章节频域上我们从"FDM"开始。
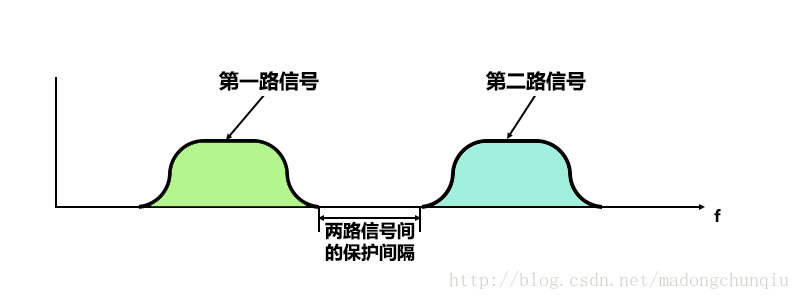
先图例一个常规FDM的系统图:
图11:常规FDM,两路信号频谱之间有间隔,互相不干扰
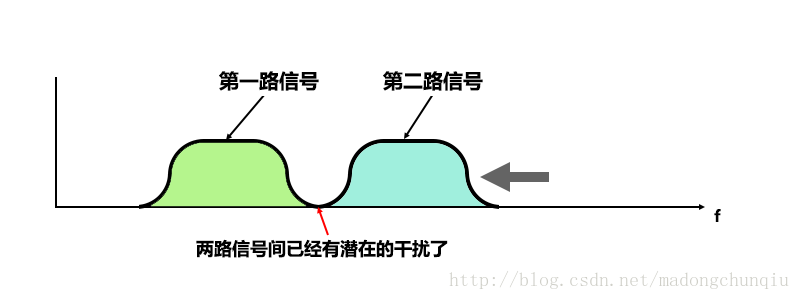
为了更好的利用系统带宽,子载波的间距可以尽量靠近些。
图12:靠得很近的FDM
实际中考虑到硬件实现,解调第一路信号时,已经很难完全去除第二路信号的影响了(电路的实现毕竟不能像剪刀裁纸一样利落),两路信号互相之间可能已经产生干扰了
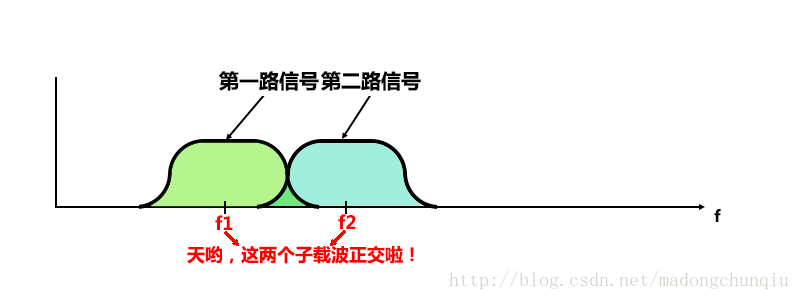
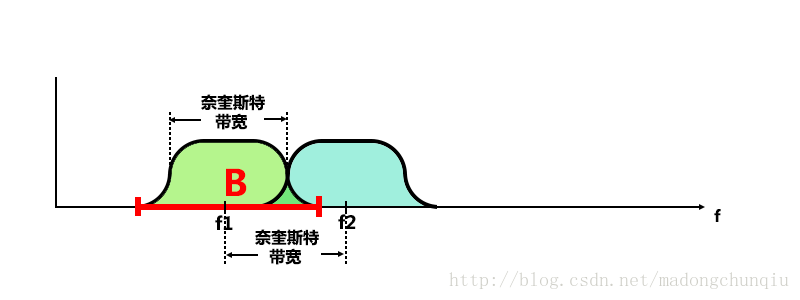
还能再近些吗?可以的。这就是OFDM的来历啊,近到完全等同于奈奎斯特带宽(后面有详述),使频带的利用率达到了理论上的最大值。
图13:继续靠近,间隔频率互相正交,因此频谱虽然有重叠,但是仍然是没有互相干扰的。神奇的OFDM
上面三个图的确有点小儿科,不知道"小白"是不是已经在心里呐喊:这谁不知道呀!不过我在这里花时间画了三张图,总还是有所考量的:
a. 作为上一个章节和本章节之间的补充和连接,说明一下OFDM在频域上面的表现,亦即OFDM的本源来历。
b. 引导思考:信号的带宽是多少?
c. 引导思考:OFDM正交频谱叠加部分到底有多宽呢?结合1.4,先想想,再往下看,会更好。
再次回到正轨,请回看第一节中的图一至图六等时域波形图,图示了在时域上,波形的调制,叠加接收,以及最终的解码。让我们看看图一至图三中的每个步骤在频域上是如何表现的。
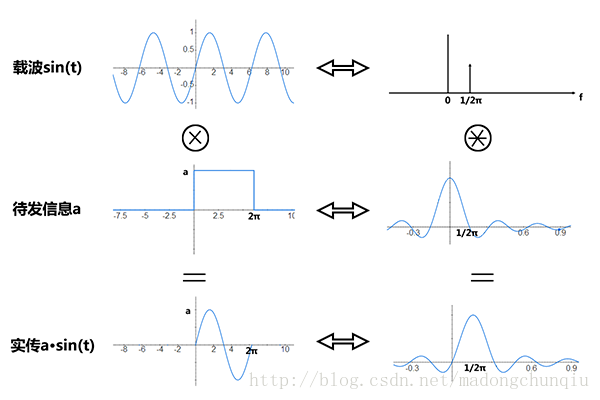
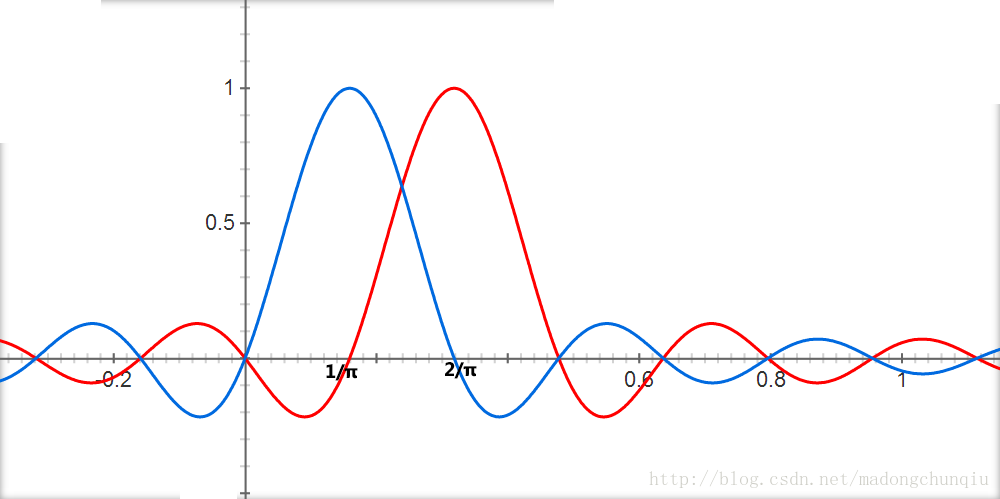
首先来看sin(t)。"小白"呀"小白",你且说说sin(t)的频谱是啥呀?"小白"弱弱的说:是一个冲激。是的,sin(t)是个单一的正弦波,代表着单一的频率,所以其频谱自然是一个冲激。不过其实图一中所示的sin(t)并不是真正的sin(t),而只是限定在[0,2π]之内的一小段。无限长度的信号被限制在一小截时间之内,【就好比从一个完整的人身上逮下一根头发,然后把整个人都丢掉,以发代人】其频谱也不再是一个冲激了。
对限制在[0,2π]内的sin(t)信号,相当于无限长的sin(t)信号乘以一个[0,2π]上的门信号(矩形脉冲),其频谱为两者频谱的卷积。sin(t)的频谱为冲激,门信号的频谱为sinc信号(即sin(x)/x信号)。冲激信号卷积sinc信号,相当于对sinc信号的搬移。所以分析到这里,可以得出图一的时域波形其对应的频谱如下:
图21:限定在[0,2π]内的a·sin(t)信号的频谱,即以sin(t)为载波的调制信号的频谱
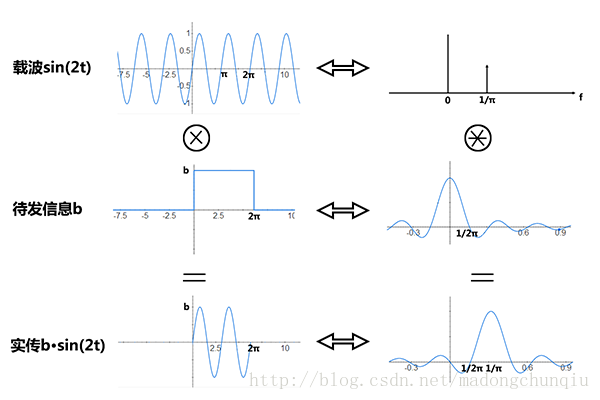
sin(2t)的频谱分析基本相同。需要注意的是,由于正交区间为[0,2π],因此sin(2t)在相同的时间内发送了两个完整波形。相同的门函数保证了两个函数的频谱形状相同,只是频谱被搬移的位置变了:
图22:限定在[0,2π]内的b·sin(2t)信号的频谱,即以sin(2t)为载波的调制信号的频谱
将sin(t)和sin(2t)所传信号的频谱叠加在一起,如下:
图23:a·sin(t)+b·sin(2t)信号的频谱
图13:继续靠近,间隔频率互相正交,因此频谱虽然有重叠,但是仍然是没有互相干扰的。神奇的OFDM
图23和图13,均是频域上两个正交子载波的频谱图。比一下,发现了吗?不太一样!
是的,想必你已经想起来了,这是因为基带信号在传输前,一般会通过脉冲成型滤波器的结果。比如使用"升余弦滚降滤波器"后,图23所示的信号就会被修理成图13所示的信号了。这样可以有效的限制带宽外部的信号,在保证本路信号没有码间串扰的情况下,既能最大限度的利用带宽,又能减少子载波间的各路信号的相互干扰。这也是1.4中没有提及的,更多的可参考[1]
贴士:脉冲成型滤波器作用于频域,可以"看作"时域中的每个码元都是以类似sinc信号发出的。没必要纠结于发送端码元的时域波形,只需要知道在接收端通过合适的采样就可以无失真的恢复信号就OK咯。
这里用到的是奈奎斯特第一准则,在下面的框框内会稍作描述:
奈奎斯特第一准则请自行google,
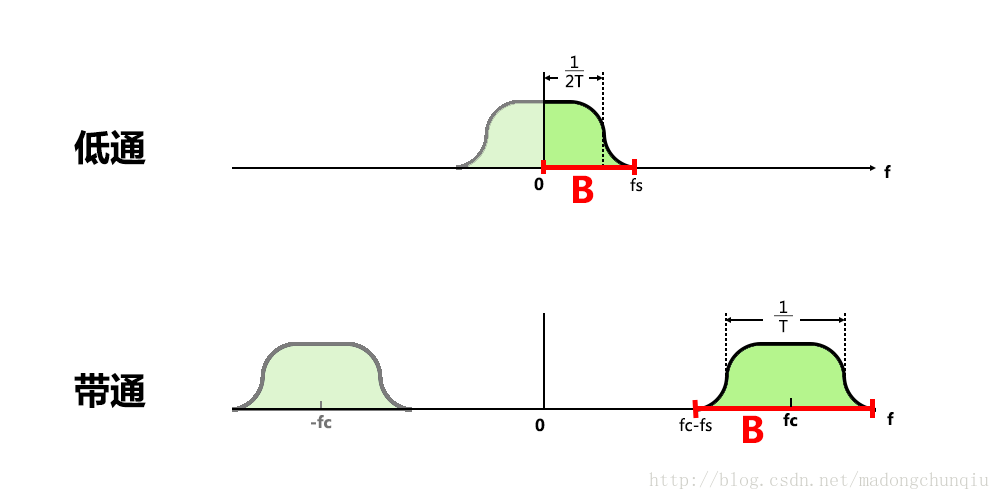
这里说说其推论:码元速率为1/T(即每个码元的传输时长为T),进行无码间串扰传输时,所需的最小带宽称为奈奎斯特带宽。
对于理想低通信道,奈奎斯特带宽W = 1/(2T)
对于理想带通信道,奈奎斯特带宽W = 1/T
在下面的图31中,可以看出信号的实际带宽B是要大于奈奎斯特带宽W(低通的1/(2T)或者带通的1/T)的,这就是理想和现实的距离。
补充说明:本文提到的"带宽",也即约定俗成的带宽理解方式,指的是信号频谱中>=0的部分。在从低通到带通的搬移过程中,因为将原信号负频率部分也移出来了(也可理解为同乘(e^{(j2πfct) }+ e^{(-j2πfct)})的结果,见参考[2]),所以带宽翻倍了。如下图所示:
图31:内涵丰富的图,请参看上面和下面的说明文字
上面专门用框框列出奈奎斯特第一准则,还有一个重要目的就是说明下频带利用率的问题。频带利用率是码元速率1/T和带宽B(或者W)的比值。
理想情况下,低通信道频带利用率为2Baud/Hz;带通信道频带利用率在传输实数信号时为1Baud/Hz,传送复数信号时为2Baud/Hz(负频率和正频率都独立携带信号)。由于讨论低通信道时往往考虑的是实数信号,而讨论带通信道时通常考虑的是复数信号,因此可以简单认为:理想情况下,信道的频带利用率为2Baud/Hz。
实际情况下,因为实际带宽B要大于奈奎斯特带宽W,所以实际FDM系统的频带利用率会低于理想情况。
【说到这里,终于可以图穷匕见了】
而OFDM的子载波间隔最低能达到奈奎斯特带宽,也就是说(在不考虑最旁边的两个子载波情况下),OFDM达到了理想信道的频带利用率。
图32:OFDM正交子载波,载频间距为奈奎斯特带宽,保证了最大的频带利用率
将上述的频域分析配上LTE的实现,有如下情况: 【注:本段描述需要有LTE物理层的基本知识】 子载波的间隔Δf=15kHz,一个OFDM symbol的发送时间是66.7us。在10MHz信道上,1ms的子帧共传输14个OFDM symbol【不是15个,留空给CP了】,每一个OFDM symbol携带600个复数信息,因此: 1. 从整个系统来看,波特率为600*14*2/1ms = 16.8MBaud,占据带宽10MHz,因此带宽利用率为16.8MBaud/10MHz = 1.68Baud/Hz,接近2Baud/Hz的理想情况。【注:一是CP占用了每个OFDM Symbol约1/15的资源,二是10MHz的频带并不是满打满算的用于传输数据,其边界频带需要留空以减少与邻近信道的干扰】 2. 单从OFDM一个symbol来看,波特率为600*2/66.7us = 18MBaud,占据带宽600*15kHz=9MHz【不考虑边界子载波带外问题】,因此其带宽利用率为18MBaud/9MHz=2Baud/Hz,符合上面的讨论。 附:5M带宽的WCDMA的chip rate = 3.84M/s,即码率为3.84M*2 = 7.68MBaud,带宽5M,所以带宽利用率为7.68MBaud/5MHz = 1.536Baud/Hz,略逊于LTE的1.68Baud/Hz【注:WCDMA的脉冲成型采用滚降系数为0.22的升余弦滤波器,奈奎斯特带宽为3.84M】章节三:用IFFT实现OFDM
其实前两章,我已经将自己的理解尽数表达了:第一节是从时域上来说子载波正交的原理;第二节是从频域上来解释子载波正交后,达到理想频带利用率的特性。想来,虽然前两章写得较长,但是应该还是很简单、清晰、易懂的。 不过"小白"的卡壳,似乎并不在于最基本的正交原理和频带利用率上,反而是IFFT变换中,充斥的各种时域频域角色变换让其眼花缭乱。
个人觉得要理解IFFT实现OFDM,最好的办法还是看公式。比如第一章节中的公式1-1和公式1-2,配上时域波形图的叠加,不要太好理解哟。
当然,这里的IFFT需要将时域离散化,因此公式(IFFT ≈ IDFT --> \ fn = 1/N·∑Fk·e(j·2π·k·n/N)) 【公式3-1,n为时域离散后的序号,N为总的IFFT个数,n∈[1,N]】
关于公式3-1的理解方法,可以是这样的。
其中一种理解方式是联系第一章节的公式1-2:可以发现公式3-1等号右侧所表达的物理意义和公式1-2是相同的,均代表了不同子载波(e^{j·2π·k·n/N})发送各自的信号Fk,然后在时域上的叠加形成fn,只不过现在叠加出来的时域不是连续波形,而是离散的时序抽样点。
另一种更容易,更可爱的理解方式是:在一个OFDM symbol的时长T内,用N个子载波各自发送一个信号F(k)(k∈[1,N]),等效于直接在时域上连续发送fn(n∈[1,N])N个信号,每个信号发送T/N的时长。
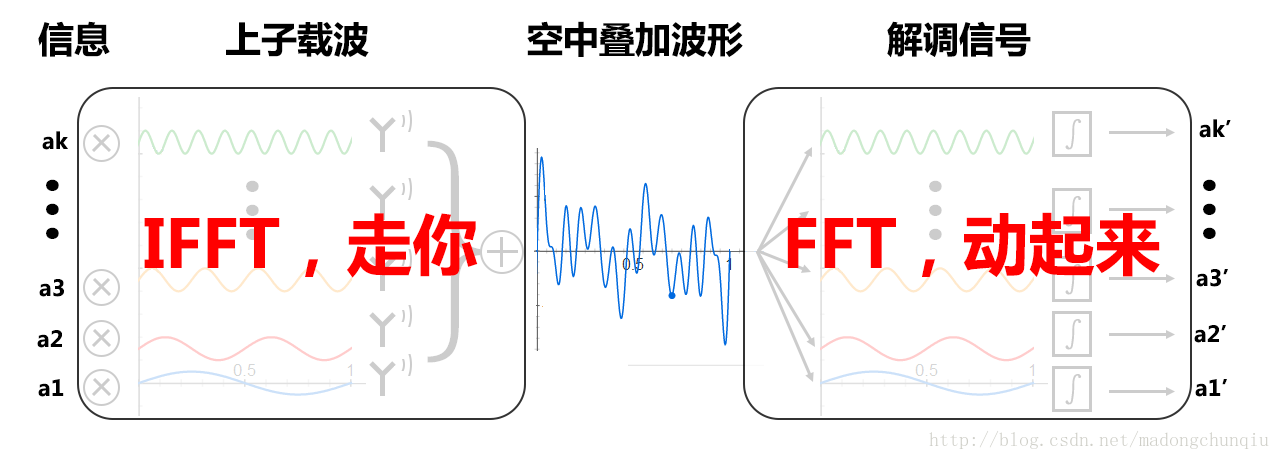
在IFFT实现OFDM中,发送端添加了IFFT模块、接收端添加了FFT模块。
IFFT模块的功能相当于说:别麻烦发送N个子载波信号了,我直接算出你们在空中会叠加成啥样子吧;FFT模块的功能相当于说:别用老式的积分方法来去除其余的正交子载波了,我帮你一次把N个携带信号全算出来吧。
就是这样,IFFT实现OFDM的系统用"数学的方法",在发送端计算信号的叠加波形,在接收端去除正交子载波,从而大大简化了系统的复杂度。
图八:用IFFT实现OFDM。请自行对比图七
最后说一句:"小白"乃"白富美"之"白",非"一穷二白"之"白"也。
好吧,该结束了。再写得长了更没人看了。
补充章节:从频谱上来看正交性
本文最开始发表时是没有这一段的,因为原文已然十分自恰,已将OFDM的原理说的非常清楚到位了。然而,这一段的内容却是别的文章中讲解OFDM时经常出现的桥段,因此觉得还是有必要补充陈述一下自己的观点。
【注:本小节为补充章节,与本文逻辑没有必然联系,可直接略过。】
从正文章节中,可以发现作者的思路:从时域角度讲解子载波的正交性;从频域角度讲解OFDM的频带利用率。作者觉得这是最容易理解OFDM原理的方式。
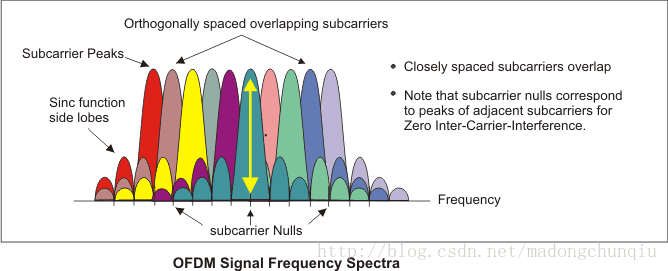
但是教材中、网络上,还有一种非常主流的讲解方式:从频域上“直观的”看待子载波的正交性。
比如下面这个图:
图51:从OFDM频谱看待正交性
这种观点的说法是:在每个子载波的抽样点上,其它的子载波信号抽样值均为0(即上图中的subcarrier Nulls对应某个子载波的Subcarrier Peak)。这种说法在图示上有非常醒目的直观效果,所以是各教材讲义中的常客,但是至少从作者的角度来看,这种说法在涉及到后面的解调信号时,将变得非常难以理解和说明。所以本文最开始的版本中是没打算写本小节的。
如果你看到这里,觉得这种说法正中下怀,那么恭喜你。
如果你看到这里,觉得这种说法已经让你的脑袋成了浆糊,那么可以回顾第一章节:时域上的正交性,然后继续阅读下面部分以解毒。
时域上的正交性和频域上的正交性之间的关系该如何联系起来呢?回顾前面提到sin(t)和sin(2t)是正交的【证明:sin(t)·sin(2t)在区间[0,2π]上的积分为0】,推广到更一般的情况是:({sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),...,sin(2π·Δf·kt)})在区间[0, 1/Δf]上正交(注:教材上一般写为u(t)在[-T/2,T/2]区间上怎么怎么着,本文就用不着那么学术了)。可以看出,这里有一个关键的参数Δf:它既是频域上子载波的间距,又确定了时域上的信号传输时间。回顾时域频域转换图:
图52:同前面的图21,时域波形和频域的转换
联系上图的时频转换,可以发现Δf既确定了子载波本身(即上图中第一排的两个图),又确定了待发信号的传输时间(即上图中第二排的两个图中信号的宽度),从而决定了信号频谱的主瓣宽度以及旁瓣为0的位置。
这也意味着,OFDM系统中一旦选定了子载波间隔,时域上的正交性以及频域上的正交性也就顺理成章的联系起来了。如下图:
图53:同前面的图23,两路信号的间隔Δf,保证了时域上的正交性、确定了频域上的旁瓣0点位置
其实对本作者而言,从频谱上来看待OFDM的正交性有点颠倒因果的嫌疑。按我的理解:OFDM选用的正交子载波是因,频谱中出现“其余子载波携带信号的旁瓣0点处于当前子载波携带信号主瓣峰值处”的现象是果。以果推因,谬矣。
继续说明:关于物理层的信号(信源编码、信道编码、信号调制)
要弄清楚信号的含义,可以将整个物理层信号传输的过程给分解开来,可以看到,不同的步骤对信号的处理是不同的。
信源编码着重于对信号的容量进行压缩,提高传输效率(比特流);
信道编码针对多变的信道插入冗余信息,增加传输的稳定性(比特流);
信号调制则是将比特流转成了特定的波形进行传输,根据调制方式的不同,即可能是一个比特对应一个波形,也有可能是数个比特对应一个波形(高阶调制)。
所以有个问题说不知道0对应什么波形,1对应什么波形,是因为没弄清调制过程。在采用比如QAM64调制后,出来的symbol就是复数了,这也是复数信号的来历。一般的文章会将一个symbol看作一个输入来看待和讨论下面的步骤,而我这篇文章因为是从sin和cos入手来讨论正交性的,因此我这篇文章中将一个symbol看成了两个实数,故而在讨论信道利用率时和主流“结论”有点出入,但其实是各自的假设不同而已。
在实际的系统中,QAM symbol 进行了针对天线阵列的precoding和资源分配的mapping后,就会进入OFDM调制了(就是上面图八的一站式IFFT计算)
继续补充:关于负频率
留言中不少关于负频率的疑问,已另作一文于此:《关于负频率的物理意义》
参考[1]: Wireless Communications, Andrea Goldsmith - 12.2 Multicarrier Modulation with Overlapping Subchannels
参考[2]: Principles of Digital Communication - Gallager - 6.4.1 Double-sideband amplitude modulation