【数论】——欧拉定理

今天摸鱼看到一道题：

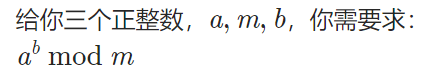
 这不就快速幂裸题吗？？

然后一看数据范围：

 ？？？这个b的范围吓到我了

经过一番学习，原来这道题考察的是：

欧拉定理&扩展欧拉定理

证明略过，直接上结论：

 

 （图源OI wiki）

那么这道题就是先处理出欧拉函数，再根据扩展欧拉求解即可。注意b要边输入边取模。

欧拉函数的处理方式：

　　类似于线性筛素数，看标程即可，很好理解。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M=1e6+10;
ll ans[M],phi[M];
ll cnt;
ll m,a,b;
void Eulersieve(){
    phi[1]=1;
    for(ll i=2;i<=m;i++){
        if(!phi[i]){
            for(ll j=i;j<=m;j+=i){
                if(!phi[j]) phi[j]=j;
                phi[j]=phi[j]/i*(i-1);
            }
        }
    }
} 
ll read(){
    ll x=0,f=1;
    char c=getchar();
    while(!isdigit(c)){
        if(c=='-') f=-1;
        c=getchar();
    } 
    while(isdigit(c)){
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}
ll getb(){
    ll x=0,flag=0;
    char c=getchar();
    while(!isdigit(c)){
        c=getchar();
    }
    while(isdigit(c)){
        x=(x*10+c-'0');
        if(x>=phi[m]){
            flag=1;
            x%=phi[m];
        }
        c=getchar();
    }
    if(x>=phi[m]){
        flag=1;
        x%=phi[m];
    }
    return flag==1?x+phi[m]:x;
}
ll qp(ll n,ll p){
    ll res=n,ans=1;
    while(p){
        if(p&1){
            ans=(res*ans)%m;
        }
        res=(res*res)%m;
        p>>=1;
    }
    return ans;
}
int main(){
    a=read();
    m=read();
    Eulersieve();
    b=getb();
    printf("%lld",qp(a,b));
    return 0;    
}