ubuntu之路——day8.2 深度学习优化算法之指数加权平均与偏差修正，以及基于指数加权移动平均法的动量梯度下降法

首先感谢吴恩达老师的免费公开课，以下图片均来自于Andrew Ng的公开课

指数加权平均法

在统计学中被称为指数加权移动平均法，来看下面一个例子：

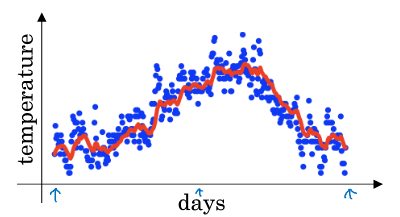
这是伦敦在一些天数中的气温分布图

V_t = βV_t-1 + (1 - β)θ_t 

β指的是加权系数 0<β<1

θ_t 指的是当前时刻的温度

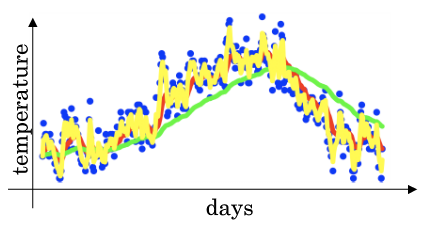
当β=0.9的时候 1/1-β = 10 所以看到上图的红线其实就是考虑了10天之内的平均气温，其拟合度较好

当β=0.98的时候 1/1-β = 50 所以上图中的绿线是考虑了50天之内的平均气温，于是这种平均气温就更加的平滑且峰值靠右，不能很好的拟合每天的温度

当β=0.5的时候 1/1-β = 2 所以上图中的黄线是考虑了2天之内的平均气温，于是这种平均气温就更加波动

偏差修正

 

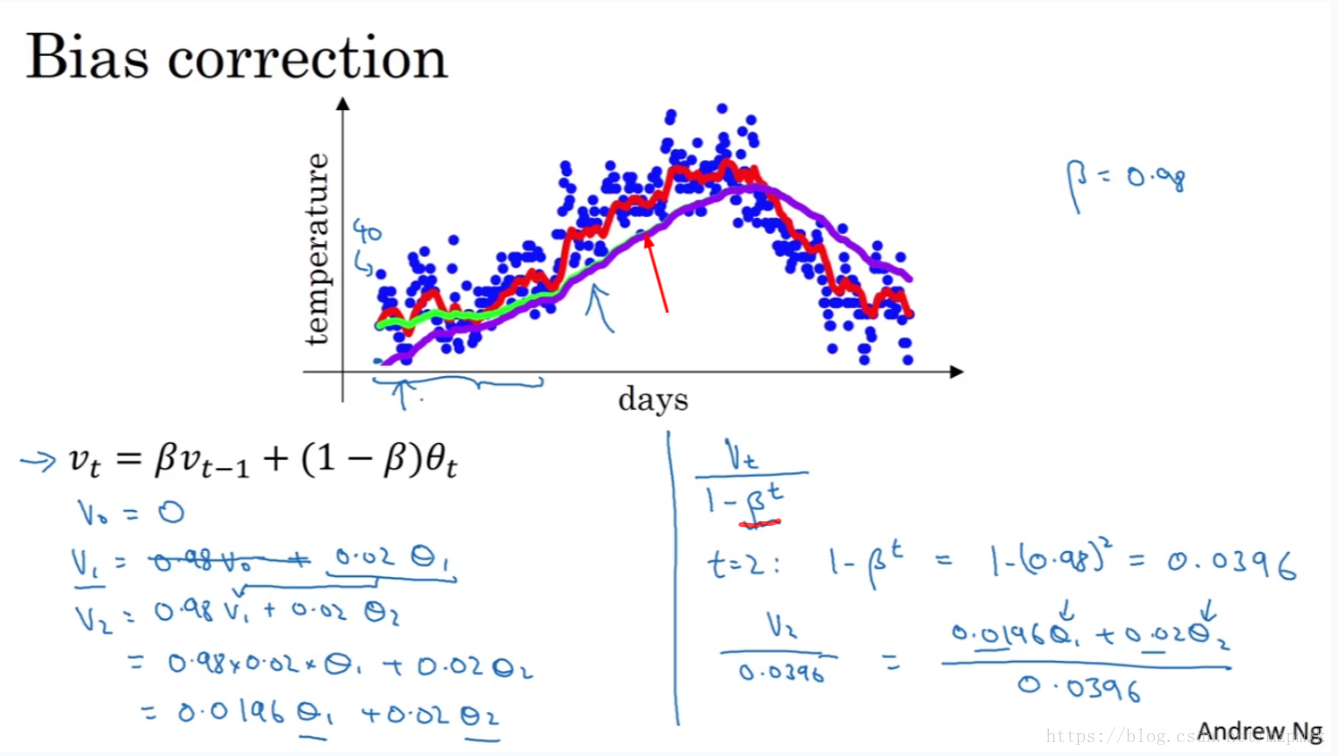
可以看到当ν₀=0时，β=0.98的时候我们真正拟合的曲线如图是紫色的，而不是我们期望得到的绿色

所以通过以下变形，使得β^t在t较小的时候能够增大θ_t的值，从而在拟合早期的时候提高拟合准确度，当然在t很大后β^t接近于0，此时的拟合度和原拟合度没有太大的区别

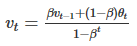
动量梯度下降法 momentum：

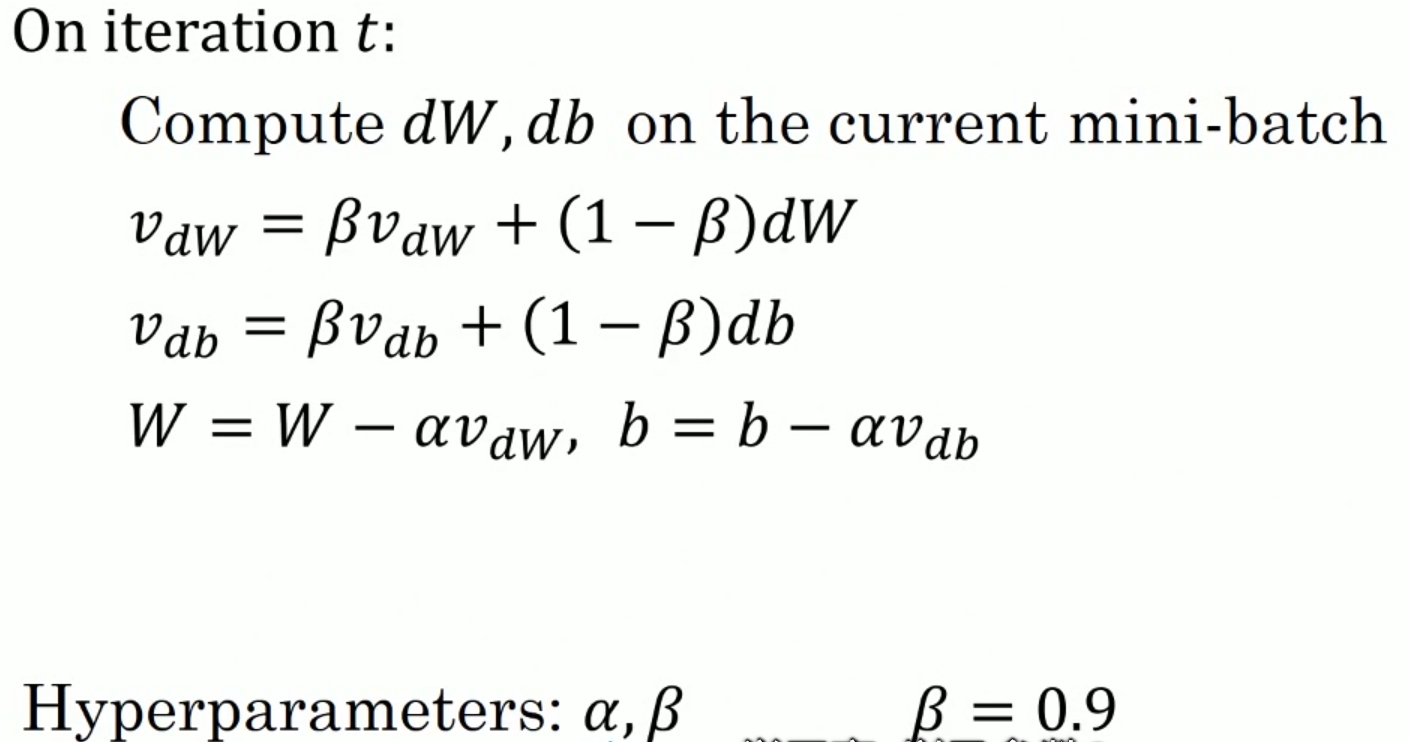
注意在动量梯度下降法中，可以忽略偏差修正带来的影响，这其实是一种加快梯度下降速度的方法