剑指Offer：数组中的逆序对

剑指Offer：数组中的逆序对

题目描述

　　在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

题目分析

　　这道题，也是我《剑指Offer》中的顽石，一直没有去动。

　　假如说某个元素X可以与其后面的元素形成逆序对，那么后面的元素肯定是比当前元素小，那后面元素的位置有序或者无序都不影响与X形成逆序对。

　　

　　那如果我们将元素分为两组，只要两组元素都是有序的，那么前面一组的某个元素A只要能和后面一组的元素B形成逆序对，那么前面一组A及A后面的元素都能与B形成逆序对。

　　

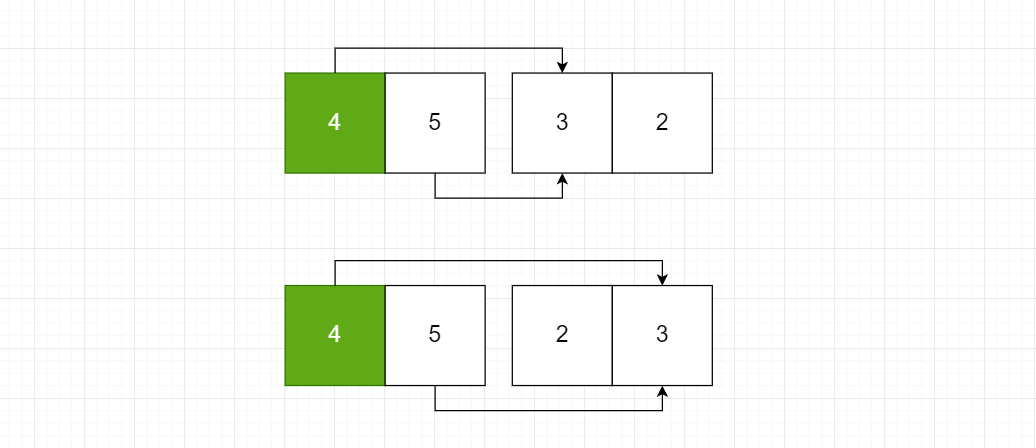
　　那我们只要在归并排序的过程中统计逆序次数即可！　　

Java题解

import java.util.Arrays;

public class Solution {
    private int count;
    public int InversePairs(int [] array) {
        count = 0;
        sort(array);
        return count;
    }

    private int[] sort(int[] nums){
        if(nums.length==1)
            return nums;
        int mid = nums.length/2;
        int[] leftNums = sort(Arrays.copyOfRange(nums,0,mid));
        int[] rightNums =sort(Arrays.copyOfRange(nums,mid,nums.length));
        return merge(leftNums,rightNums);
    }


    /**
     * 合并操作
     * @param leftNums
     * @param rightNums
     */
    private int[] merge(int[] leftNums, int[] rightNums){
        int[] result = new int[leftNums.length+rightNums.length];
        int i=0,j=0,p=0;
        while (i<leftNums.length&&j<rightNums.length){
            if(leftNums[i]<rightNums[j]){
                result[p] = leftNums[i];
                i++;
            }else{
                count+=(leftNums.length-i);
                count %= 1000000007;
                result[p] = rightNums[j];
                j++;
            }
            p++;
        }
        while (i<leftNums.length)
            result[p++]=leftNums[i++];
        while (j<rightNums.length)
            result[p++]=rightNums[j++];
        return result;
    }
}