二分图是一种特殊的图论模型,什么是二分图呢?我们知道图是由点集和边集构成的,如果可以把图的点集分成两部分,而图中的每条边都是一个端点属于其中一个集合,另一个端点属于另一个集合,我们把这样的图称为二分图(严谨定义请自行百度)。二分图有什么性质呢?二分图可以做到,给每个结点染色(只染成两种颜色),不会出现相邻的结点颜色相同的情况。因为二分图可以被划分成上述的两个集合,给其中一个集合染上一种颜色,给另一个集合染上另一种颜色,那么每条边的两端都是不同颜色的点,因此不会出现相邻结点颜色相同的情况。同样的,二分图染色其实就是把图划分成这么两个集合的过程。
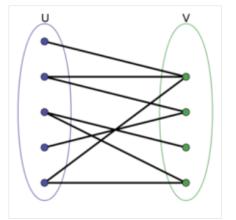
给一个图进行二分图染色的过程也可以顺便判断一个图是不是二分图,这是因为二分图一定可以进行二分图染色,可以进行二分图染色的一定是二分图。那么如果我们在染色过程中遇到冲突的话(两个相邻结点颜色相同),就说明这不是一个二分图。二分图染色类似于图的遍历,可以使用DFS或BFS,这里呢,我用的是BFS。对每个结点进行染色,尽量染成与相邻结点不同的颜色,但如果存在冲突,则不是二分图,否则可以一直染色下去,将点划分成两个集合。
附一道模板题:https://www.luogu.org/problemnew/show/P1330
做这道题时,我还不会二分图染色,就用了贪心,每次删除度最大的点,只有40分。学了二分图染色后,发现这就是个简单的模板题。因为要保证每个放河蟹的点不能相邻,其实就是一个二分图染色问题,不过是需要统计染上两种颜色的点中,最少的那一类点。另外,图不保证连通,对于每个连通块都要进行一次染色,分别统计答案。

1 #include <cstdio> 2 #include <cstdlib> 3 #include <algorithm> 4 #include <queue> 5 6 using namespace std; 7 8 inline int get_num() { 9 int num = 0; 10 char c = getchar(); 11 while (c < '0' || c > '9') c = getchar(); 12 while (c >= '0' && c <= '9') 13 num = num * 10 + c - '0', c = getchar(); 14 return num; 15 } 16 17 const int maxn = 1e4 + 5, maxm = 1e5 + 5; 18 19 int head[maxn], eid; 20 21 struct Edge { 22 int v, next; 23 } edge[2 * maxm]; 24 25 inline void insert(int u, int v) { 26 edge[++eid].v = v; 27 edge[eid].next = head[u]; 28 head[u] = eid; 29 } 30 31 int vis[maxn], cnt[3], ans; 32 33 queue<int> q; 34 35 inline void bfs(int s) { 36 cnt[1] = 1, cnt[2] = 0; 37 vis[s] = 1; 38 q.push(s); 39 while (!q.empty()) { 40 int u = q.front(); 41 q.pop(); 42 for (int p = head[u]; p; p = edge[p].next) { 43 int v = edge[p].v; 44 if (vis[v] && vis[v] == vis[u]) { 45 printf("Impossible"); 46 exit(0); 47 } else if (!vis[v]) { 48 vis[v] = vis[u] % 2 + 1; 49 ++cnt[vis[v]]; 50 q.push(v); 51 } 52 } 53 } 54 ans += min(cnt[1], cnt[2]); 55 } 56 57 int main() { 58 int n = get_num(), m = get_num(); 59 for (int i = 1; i <= m; ++i) { 60 int a = get_num(), b = get_num(); 61 insert(a, b); 62 insert(b, a); 63 } 64 for (int i = 1; i <= n; ++i) 65 if (!vis[i]) bfs(i); 66 printf("%d", ans); 67 return 0; 68 }
