================================================
首先自作多情的说一句——“抱歉!”
古语“有志者、事竟成”,是说有志向的人最终都能够成事。想到这句话我很惭愧,我居然连这样一件小事都无法坚持不懈的完成,这个系列的博客我一拖再拖,一个多月里竟然再没有更新。虽然博客鲜有看客垂阅,但是这半途而废的事实却是明显的。痛定思痛,我决定老老实实更完。算是亡羊补牢,做到有始有终吧。
================================================
---内容开始--
上一节,我们介绍了SC译码过程中的两个解码特例——u1和u2,通过这两例解码方案的介绍,我们对于利用Arikan递推公式进行串行消除解码的过程有了一个初步的认识,接下来我们的任务在于由特殊到一般,归纳出适用于所有解码器节点的解码方案,并给出相应的matlab代码。
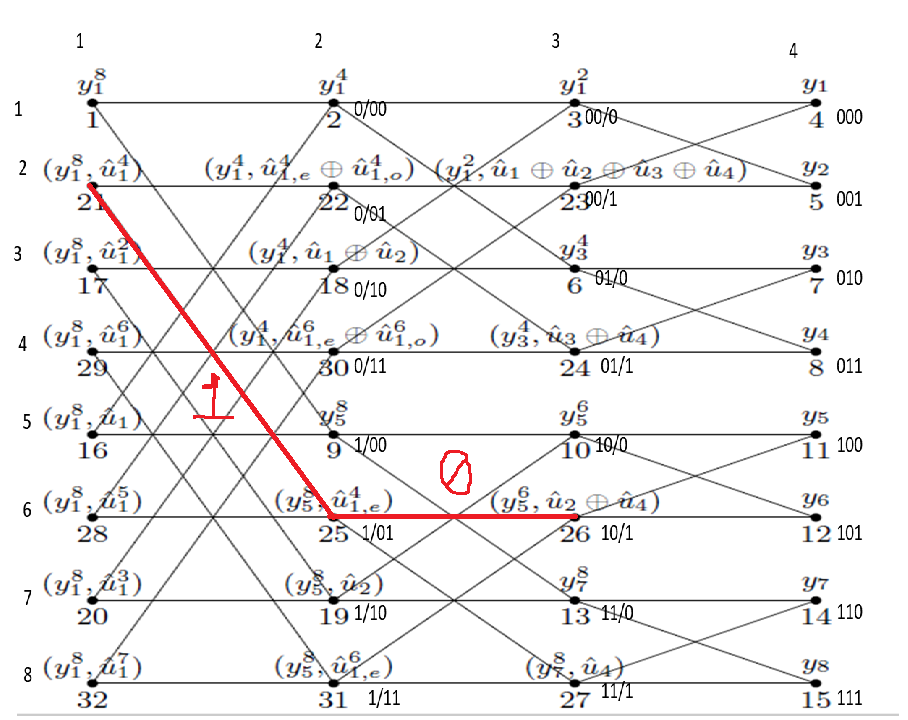
我们先来重新观察蝶形解码图:
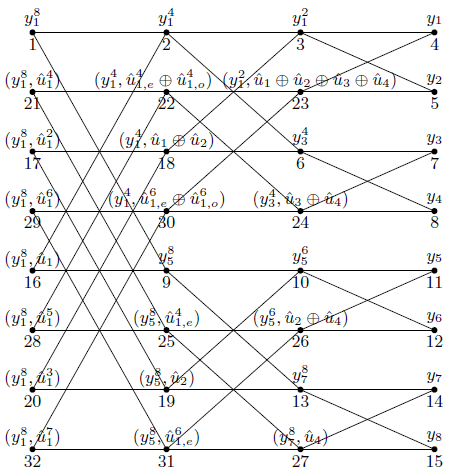
根究u1、u2的解码经验,我们可以将解码过程作如下归纳:
① 判断要解出的节点为上节点还是下节点,若为上节点则进行步骤②,否则进行步骤③;
② 根据解码图中前后节点的坐标关系,找到该节点所开启的两个节点,分别判断这两个节点是否被解出,如果未解出回到步骤①,否则直接利用上节点计算公式求得该节点似然值。
③ 判断相应上节点是否解出,如果未解出,执行步骤②,否则执行步骤④计算指数项;
(根据我们多次提到的原则——左上节点和左下节点总是同时被解出,一般情况下在求解下节点的时候,相应的上节点已经解出。)
④ 我们先来复习一下什么是指数项
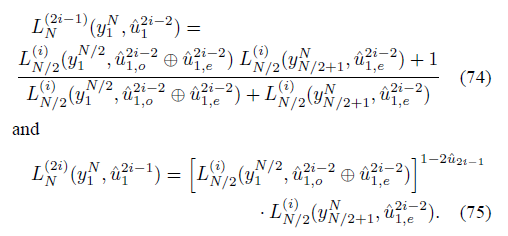
如上图为Arikan译码递推公式。对于蝶形的左下节点的求解,在得到左上节点似然值的基础上使用第二个公式。其中,指数项为![]() 。
。
【关于指数项计算的专业内容,读者可参考论文《极化码编码与译码算法研究》...王继伟...第3.3.1.3节】
这个指数项在随着迭代N-->N/2-->N/4-->...将发生变化。由于博主水平有限,无法很好的表述推导过程,这里偷个懒,直接将结论写在下面。读者如果对于结论的导出有更深入的需要,请移步上述论文相关章节。
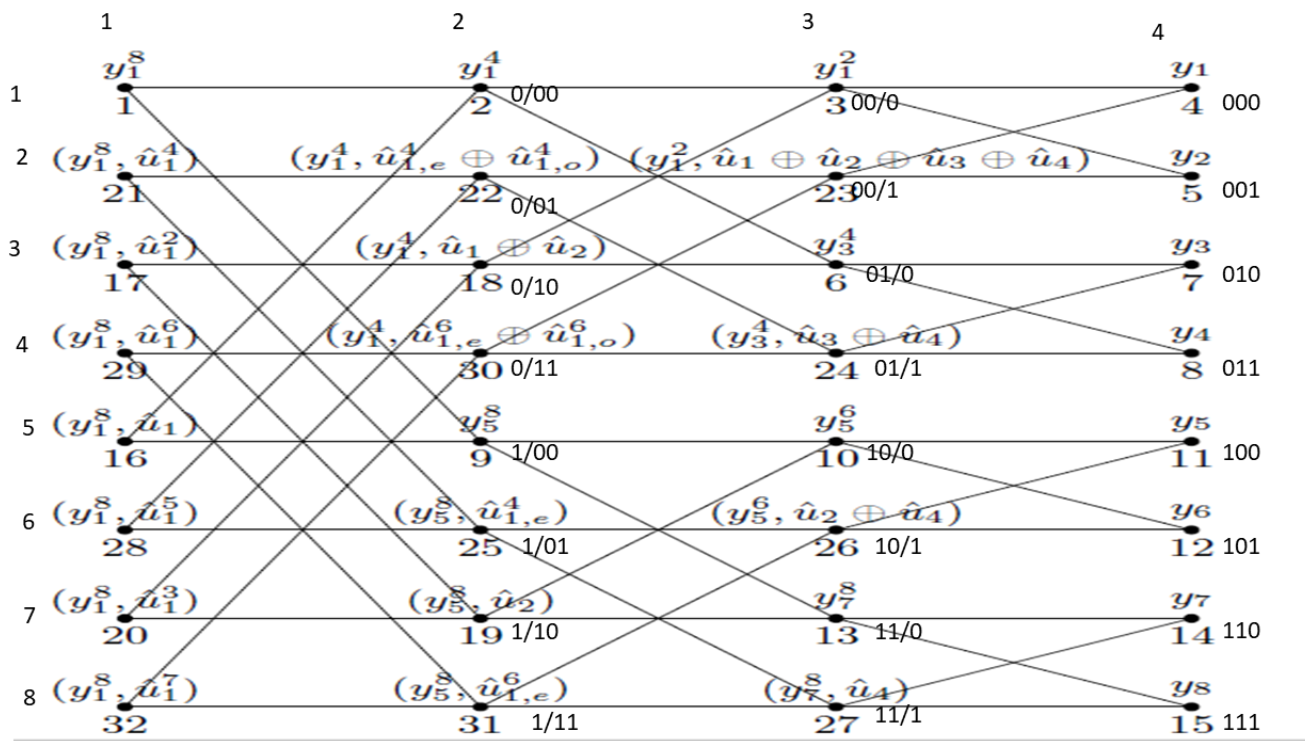
如上图所示为n=3,N=8时的解码图,不同的是,我们给每一个节点提供了第三个标签。(除去第一列和最后一列)将节点所在行数减一后转化为长度为n的二进制数,自第二行开始将二进制数用斜杠 ‘ / ’ 加以分割,斜杠放置位置的规律显然可见。经过这样的处理以后,我们可以观察一个非常明显的现象,观察每个斜杠后的比特,比特为0代表该节点为上节点,比特为1代表该节点为下节点。
下面来关注指数项的求解。观察斜杠前后的比特:
- 为了求解指数项,自左向右,我们定义操作“1”为抽取向量中的偶数位,组成长度减半的新向量;定义操作“0”为分别抽取向量中的偶数位与奇数位组成两个新向量,然后将它们按位异或,得到长度减半的新向量。(这部分会通过一个例子详细说明,看不懂不要捉急=v=)
- 为了确定解码图中的某个节点由哪个解码器所启动,自右向左,我们定义操作“1”为向左上寻找节点;定义操作“0”为向左寻找节点。(这里我们回顾一下上一节提到的前后节点之间的关系:
设当前节点坐标为(i,j),若当前节点未左上蝶形,则这个节点开启的两个节点的坐标为(i,j+1)和(i+N/2j,j+1)。若为左下节点,则这两个节点开启的两个节点坐标为(i,j+1)和(i-N/2j,j+1))
因此,利用反推的道理,对于所求解的节点 (i,j) ,从斜杠处开始,自右向左,遇到比特“0”则向左寻找一位 (i,j-1),遇到比特“1”则向左上寻找 (i-N/2j,j-1)。
下面,我们以节点26为例详细说一下。该节点的三个标签分别为“26”, ,“10/1”。第一个标签指代该节点的求解顺序,第二个标签描述该节点的似然值通过计算
,“10/1”。第一个标签指代该节点的求解顺序,第二个标签描述该节点的似然值通过计算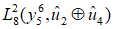 得到,其中
得到,其中 即为指数项。通过第三个标签,我们可以知道为什么指数项是
即为指数项。通过第三个标签,我们可以知道为什么指数项是 。观察“10/1”,斜杠前有两位“10”。首先,我们来判断,节点26由哪一个节点所开启,自右向左,第一位遇到“0”,往左移动一位;第二位遇到“1”,往左上寻找。最后发现找到的是节点21,观察发现此时已经解出的解码器为
。观察“10/1”,斜杠前有两位“10”。首先,我们来判断,节点26由哪一个节点所开启,自右向左,第一位遇到“0”,往左移动一位;第二位遇到“1”,往左上寻找。最后发现找到的是节点21,观察发现此时已经解出的解码器为 。得到这一信息后,我们来求解指数项,自左向右,第一位遇到“1”,抽取偶数位组成向量(u2,u4);第二位遇到“0”,抽取奇数位——u2,偶数位——u4,按位异或——
。得到这一信息后,我们来求解指数项,自左向右,第一位遇到“1”,抽取偶数位组成向量(u2,u4);第二位遇到“0”,抽取奇数位——u2,偶数位——u4,按位异或—— 。
。
对于解码器中所有的节点,在以上办法的指导下,通过坐标变换和少量的位运算,即可在必要情况下求解相应节点的指数项。
求得指数项之后返回文章最开始的流程之中,我们可以依次求解出解码图中所有节点的似然值,最后对解码器进行似然判决(包含硬判决与软判决)。
判决后所得到的比特流即为原比特流在极化码系统下仿真得到的结果,通过逐位比对,统计传输前后的比特差异,我们可以得到一系列的误码指标来表征系统性能。
我们来回顾一下本节中的重点:
1、本节,我们旨在解决如何求解解码图中的节点似然值。
2、我们根据似然值计算递推公式,将节点分为上节点和下节点,上节点可以直接求解,下节点需要计算指数项。
3、通过判断前后节点坐标关系以及定义“1”、“0”两种位运算,我们实现了求解所需任意节点的指数项。
4、通过似然判决以及统计比特误码率,我们得到了系统的仿真性能。
关于极化码,一些入门的论文如下:
【1】Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels.作者 Erdal Arıkan。Arikan教授是极化码的缔造者,这篇论文发表在IEEE上,也是第一篇对极化码及相关理论进行系统而详尽阐明的权威论文。
【2】极化码编码与译码算法研究.作者 王继伟。对于很多人来说,英文文献阅读起来比较吃力,好在一些质量较高的中文文献中对极化码有非常详尽的介绍,其内容之丰富,足以作为研究Arikan论文的有力辅助。
【3】极化码的译码算法研究及其应用.作者 张亮。这是一篇博士学位论文,内容充实详尽、专业严谨,文末对于极化码存在的一些问题进行了分析和展望,很有启发性。
这些文章在知网、万方等数据库中均可获取,在极化码的研究论文中,这三篇只是沧海一粟,还有很多国内外学者的文章值得借鉴,不再啰嗦列举。
这是本系列的最后一篇文章。开始时雄心壮志,结束却时草草收笔,未免有些遗憾。在撰写博文的过程中,我发现了很多之前没有注意到的问题,收获不可谓不硕大。论语云,“温故而知新”,诚不我欺!