11.5 | 学习笔记

记录今天A的两个题

https://codeforces.com/contest/1395/problem/D

给你n个数字，当某一个n大于零的时候，他后面的d个数字都会变成0，问怎样排布能让数列总和最大

要尽可能大，思路是首先将n分为合法和不合法两类，

在Du被禁言的时候，不管取多少后面的d天都被禁言了，那为了给和贡献最大，破罐子破摔取最大的，

在其他可以畅所欲言的时候，为了给和贡献最大，就要在违法的边缘试探，同样尽量取合法值里面最大的，

我的想法是枚举可以被禁言的次数，注意这里要上取整，同时最后一天必然被禁言，否则的话同等条件下，在最后一次被禁言的那天到最后一天就对和没有贡献，那莫不如先让他前几天贡献，最后一天禁言，注意这里的表达式，n-(i-1)*(d+1)-1（最后那个1就是最后一次被禁言）那么这里i=0时n-1=-1显然是没有意义的，所以可以在循环外面将ans赋值成禁言0次的情况，但是需要注意，这里的ans并不是答案，只是一个下限，因为大多数情况下不能保证每个数都比m小，加这个是为了防止出现这种特殊情况，注意前缀和的使用可以降低求和的时间复杂度：

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
typedef long long int ll;
ll d,n,m,tmp,cnt,x,y,res,ans;
ll ud[maxn],ov[maxn];

int main()
{
    cin>>n>>d>>m;
    d++;// 由于d后来每次出现都是d+1,所以一开始直接++
    for(int i=0;i<n;i++)
    {
        cin>>tmp;
        if(tmp>m)ov[++x]=tmp; // 不合法类
        else ud[++y]=tmp; // 合法类
    }
    cnt=ceil(1.0*n/d);
    sort(ov+1,ov+x+1,greater<ll>()); // 降序，下同
    sort(ud+1,ud+y+1,greater<ll>());
    for(int i=1;i<=x;i++)
        ov[i]+=ov[i-1];
    for(int i=1;i<=y;i++)
        ud[i]+=ud[i-1];
    ans=ud[y];
    for(int i=1;i<=cnt;i++)
    {
        res=ov[i];
        res+=ud[min(y,n-(i-1)*d-1)];
        if(res>ans)ans=res;
    }
    cout<<ans<<endl;
    return 0;
}

https://codeforces.com/contest/1443/problem/D

这题一开始不会，某北极熊给了很好的思路，抽象为判断能否将给定序列拆分成一个非递增序列和非递减序列，

假设A为递减序列，B为递增序列，那么为了尽可能满足条件，每次尽量给A多分一部分，给B少分一部分，这样才不会给后来项的拆分添麻烦

（通俗来讲就是我前面的项为了满足条件已经很够意思了，你后面的再不行就直接判断不合法滚粗）

每次输入一个数，判断这个数和上次剩下的数的关系，如果小于直接判断不合法；

如果合法，先给B预留出一部分，这部分要尽可能小，也就是给A留的尽可能大，但是问题在可能B可以了但是剩下的给A的太多了导致A不能递减，那就在满足A的条件下给B多分点，上图：

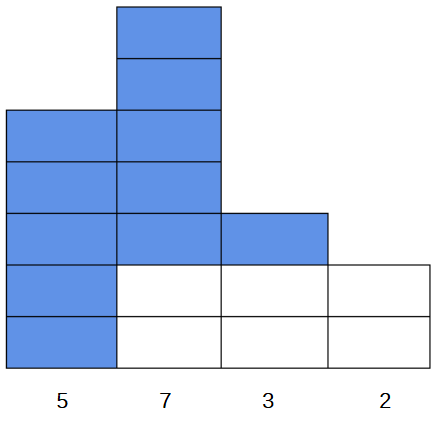
 以第二列为例，刚才给B分的是0，A是5，首先看能不能再给B分0，这时候发现A分了7，大于5不合法，所以只能给A分5，这样B不得已增到2，

同理第三列，能不能给B分2，发现这样的话A分1，合理，依此类推...

所以到后来甚至数组都不用存了，直接循环：

#include <bits/stdc++.h>
using namespace std;
int t,n,gap,lef,now,flag; // gap上次减掉的，lef上次剩下的

int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>gap;
        flag=1;lef=0;
        while(--n)
        {
            cin>>now;
            if(now<lef)
                flag=0;
            else
            {
                gap=min(gap,now-lef);
                lef=now-gap;
            }
        }
        cout<<(flag?"Yes
":"No
");
    }
    return 0;
}