很容易想到,相对于直线 l1,斜率较大的直线 l2 一定在这两条直线的交点的右侧将l1 覆盖掉,而l2在交点的左侧部分会被l1覆盖。这样的话,对于三条直线l1, l2, l3 满足k1 < k2 < k3, 设l1和l2的交点为A, l1和l3的交点为B, l2和l3的交点为 C,如果B在A的左侧,那么l2就会被完全覆盖掉,因为C一定在B的左侧若果只有l2 和 l3,那么l2的露出部分只有在C的左侧,而因为在B的左侧l2已经被l1覆盖,所以得出结论,l2一定被覆盖了。
上面说的其实就是这个情况……
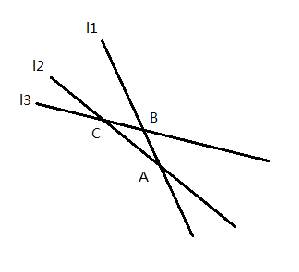
我们可以用一个单调栈实现这个比较,只要比较当前直线和栈顶top - 1的交点A和top和top - 1的交点B,如果A的横坐标小于B,就将top弹出。
最后要考虑的是判重,若果斜率相同,那么一定是b小的被覆盖了,所以排序的时候当斜率相同时,b大的优先,这样在操作的时候如果斜率相同就可以直接continue了。

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cctype> 8 #include<vector> 9 #include<stack> 10 #include<queue> 11 using namespace std; 12 #define enter printf(" ") 13 #define space printf(" ") 14 #define Mem(a) memset(a, 0, sizeof(a)) 15 typedef long long ll; 16 typedef double db; 17 const int INF = 0x3f3f3f3f; 18 const int eps = 1e-8; 19 const int maxn = 5e4 + 5; 20 inline ll read() 21 { 22 ll ans = 0; 23 char ch = getchar(), last = ' '; 24 while(!isdigit(ch)) {last = ch; ch = getchar();} 25 while(isdigit(ch)) 26 { 27 ans = ans * 10 + ch - '0'; ch = getchar(); 28 } 29 if(last == '-') ans = -ans; 30 return ans; 31 } 32 inline void write(ll x) 33 { 34 if(x < 0) x = -x, putchar('-'); 35 if(x >= 10) write(x / 10); 36 putchar(x % 10 + '0'); 37 } 38 39 int n; 40 struct Node 41 { 42 db a, b; 43 int id; 44 bool operator < (const Node& other)const 45 { 46 return a < other.a || (a == other.a && b > other.b); 47 } 48 }t[maxn]; 49 50 Node st[maxn]; 51 int top = 0; 52 db cal(Node& x, Node& y) 53 { 54 return (y.b - x. b) / (x.a - y.a); //交点的横坐标 55 } 56 57 bool vis[maxn]; 58 59 int main() 60 { 61 n = read(); 62 for(int i = 1; i <= n; ++i) {t[i].a = read(); t[i].b = read(); t[i].id = i;} 63 sort(t + 1, t + n + 1); 64 for(int i = 1; i <= n; ++i) 65 { 66 if(top && st[top].a == t[i].a) continue; 67 while(top > 1 && cal(st[top - 1], t[i]) <= cal(st[top], st[top - 1]) + eps) top--; 68 st[++top] = t[i]; 69 } 70 while(top > 0) vis[st[top--].id] = 1; 71 for(int i = 1; i <= n; ++i) if(vis[i]) {write(i); space;} enter; 72 return 0; 73 }
